MRD:anythingpg2116
Dynamics of H+H2 system
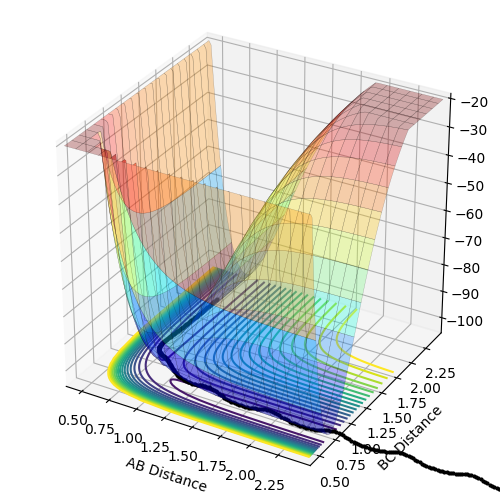
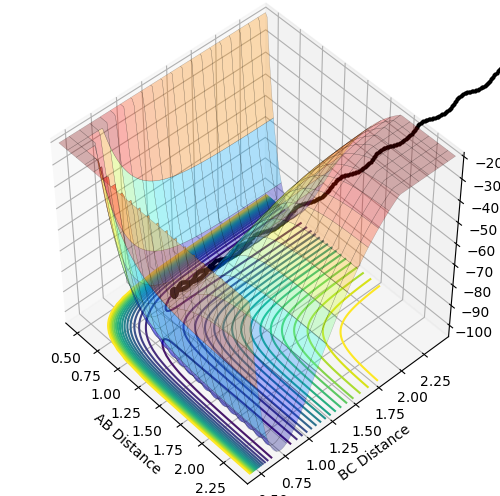
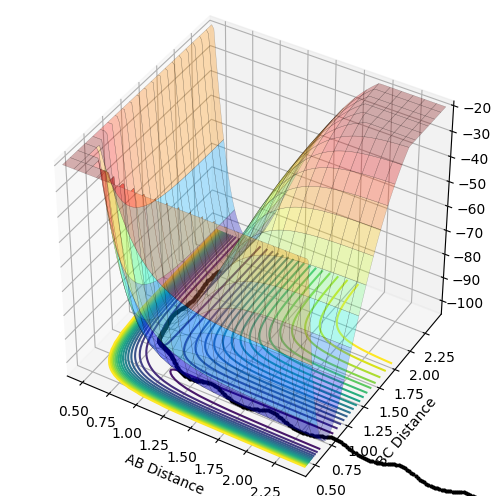
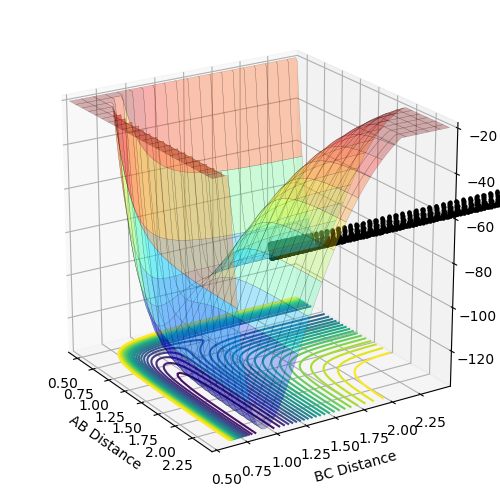
Potential energy surface as a function of two variables
The potential energy surface is a function of two variables: r1 and r2. Functions of two variables can show three different points: minimum, maximum and a saddle point. Local minimum is a point at which the function has the smallest value for given r1 and r2 values. Therefore, the gradient of the tangent with respect to both variables at this point equals zero (the same applies to the maximum except it is the largest value for given r1 and r2). The saddle point, which in this case is the location of the transition structure, is a point of the potential surface at which the function appears to reach a local minimum with respect to one of the variables and a local maximum with respect to the other variable. Therefore, the gradient of the tangent with respect to both variables is zero, too. Since all the gradients at the minimum and saddle point equal zero, these two points cannot be distinguished by the first derivative of the function. This needs to be done by looking at the curvature of the potential surface around these points, which is related to the second derivative of the function. At the minimum, the second derivative with respect to both variables is positive so the function appears to be concave up in both directions around this point. At the saddle point, the second derivative with respect to one variable is positive and negative with respect to the other one so the function appears to be concave up in one direction and concave down in the other.
Ng611 (talk) 15:12, 1 June 2018 (BST) A good general definition of a saddle point here. What do you mean when you say 'variables' though? What are your variables here? Some additional explanation or perhaps even a diagram would be very helpful here.
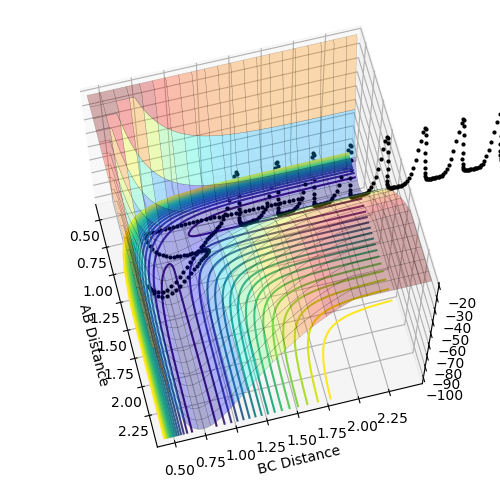
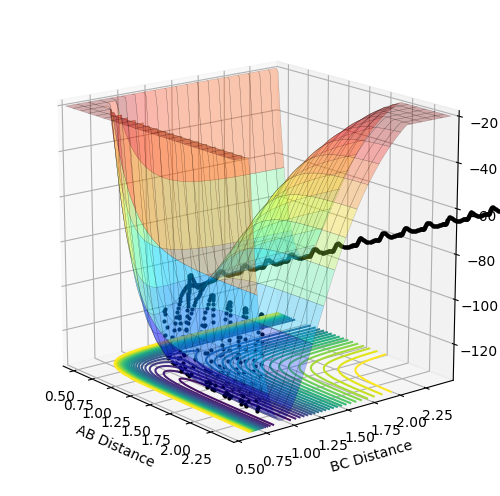
Finding the transition state
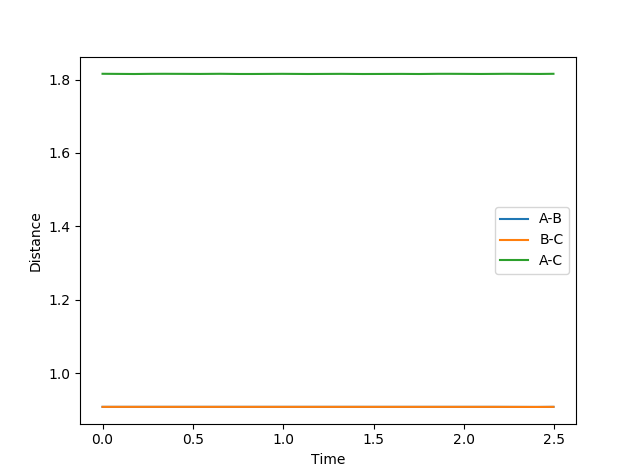
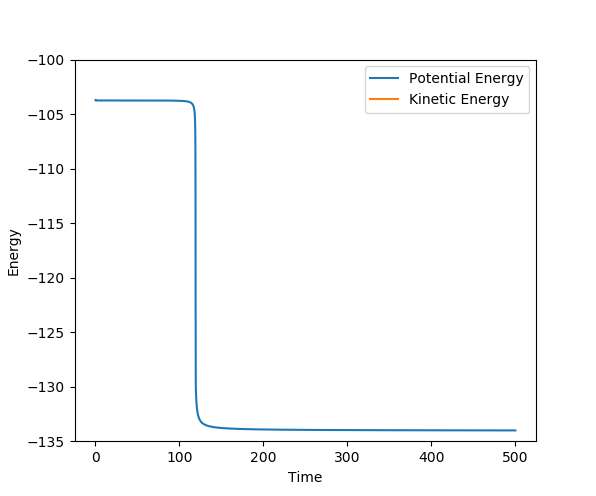
The distance was estimated to be 0.9079 Å. At this point, there is very limited oscillation around the ridge which indicates that the system is very close to the saddle point of the potential surface. Also, the limited oscillation is reflected in the internuclear distances vs. time plot which shows two straight lines (variation in A-B distance overlaps with B-C distance since they vary in the same way): this proves that the force acting on the system is very close to zero, as there is virtually no vibrating related to A-B or B-C, so the system must be very close to the saddle point of the potential energy surface, i.e. the transition state.
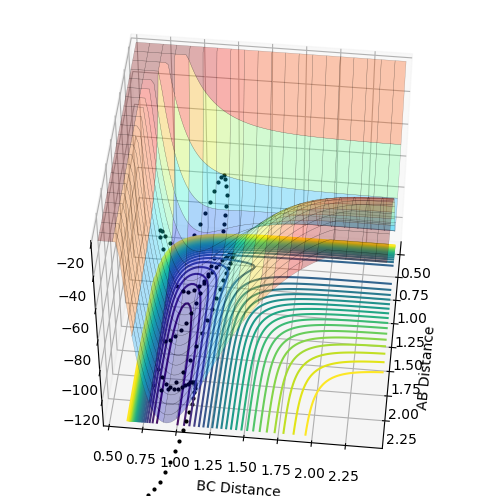
Distinguishing between the "dynamics trajectory" and MEP
The difference is that the "dynamics trajectory" is wavy so the B-C distance oscillates while the B-C molecule is getting more distant from atom A. This gives a more realistic view of the system as atoms in molecules are not static. The reaction path, on the other hand, does not take the vibrations into account as it corresponds to the minimum energy trajectory so it is a "non-wavy" line that goes along the valley floor. If it was wavy, it would not correspond to the minimum energy trajectory as the potential energy would oscillate and hence would not be minimal at every instant.
Ng611 (talk) 15:13, 1 June 2018 (BST) Good. Specifically, the MEP trajectory resets the momentum to zero after each timestep.
Reactive and unreactive trajectories
| p1 | p2 | Total energy [kcal/mol] | Trajectory |
|---|---|---|---|
| -1.25 | -2.5 | -99.018 | reactive |
| -1.5 | -2.0 | -100.456 | unreactive |
| -1.5 | -2.5 | -98.956 | reactive |
| -2.5 | -5.0 | -84.956 | unreactive |
| -2.5 | -5.2 | -83.416 | reactive |
Case 1: H2 slightly vibrates (almost no vibrations) as it approaches H. Once they get close enough, an exchange of an atom takes place and the new H2 molecule leaves the "complex" with significant vibrations.
Case 2: The vibrating H2 molecule is getting closer to the H atom but they do not have sufficiently high momentum to come close enough to reach and overcome the transition state so the reactants cannot interact and no substitution takes place.
Case 3: The conditions are the same as in case 2 but now the H atom has a more negative momentum which gives it a velocity high enough to come close the to the H2 molecule and overcome the transition state so the substitution takes place.
Case 4: The H2 molecule, barely vibrating, approaches the H atom and the transition state is overcome (so the substitution takes place) but the resulting conformation of the system is not stable enough so the system returns back to the reactants.
Case 5: In this case, the reaction proceeds in the same way as in case 4 but now the system formed by the returning to the reactants is not stable enough either and collapses to the products where it reaches a more stable conformation and stays there so the substitution eventually does take place.
Transition state theory
Transition state theory has the following assumptions[1]:
1.) The nuclear and electronic motions can be separated (equivalent to the Born-Oppenheimer approximation).
2.) Boltzmann distribution can be used to model the energy distribution associated with the reacting particles.
3.) When molecular systems cross the transition state towards the products, they cannot return and reform the reactants.
4.) In the transition state, motion along the reaction coordinate may be separated from the other motions and treated classically as a translation.
As proved in the previous section in case 4, the third assumption of the TST is not always true since the system can return to the reactants after crossing the transition state. This means that a certain fraction of systems that have crossed transition states does not result in the formation of products so the actual (experimental) rate can be slower than the one predicted by this theory. On the other hand, the fourth assumption, which is based on classical mechanics, rejects the possibility of tunneling which is a quantum mechanical phenomenon. In this phenomenon, particles can "tunnel through" an energetic barrier, even if they do not have enough energy to overcome it. Therefore, TST does not take into account this additional reaction pathway so, with respect to the fourth assumption, it predicts a slower rate than the experimental one might be. However, the tunneling effect is generally less significant than transition state recrossing (even though it gets more significant for low barrier reactions) so it can be concluded that rates predicted by TST are generally faster than the experimental ones.
Ng611 (talk) 15:14, 1 June 2018 (BST) Excellent explanation!
Dynamics of the F-H-H system
Exothermic vs. endothermic reaction
F + H2 is exothermic because there is a large drop in potential energy after the substitution proceeds. Therefore, H + HF, which is the reverse process, is endothermic. Whether a reaction is exothermic or endothermic depends on the bond strengths: exothermic reactions involve breaking of a weak bond and formation of a strong bond because the energy released upon the strong bond formation can offset the energy required to break the weak bond; the excess energy is lost as heat. In endothermic reactions, the opposite happens: the low amount of energy released when a weak bond is formed is not sufficient to break the strong bond so energy has to be supplied from the surroundings. In this case, the F-H bond is stronger than the H-H bond due to the ionic contribution resulting from the relatively high difference in electronegativities so the reaction F + H2 is exothermic.
Finding the transition state
r(H-H) 0.745 Å, r(H-F) 1.8107 Å. The process of finding the transition state was basically the same as in the H+H2 system. The only difference was that the potential surface is not symmetrical (since the reactants and products are not chemically equivalent) so the transition state could not be located at the same A-B and B-C distances. Instead, the approximate location had to be established first: this was done by applying the Hammond's postulate which states that exothermic reactions have an early transition state, i.e transition state which is on the reaction coordinate closer to the reactants as they are energetically more similar. The location of the transition state is illustrated below by the potential surface and internuclear distances vs. time plot:
Determining the activation energies
To determine Ea for H2 + F, the H-H distance was increased by 0.01 relative to the transition state, 100000 steps were selected for the MEP calculation and energy vs. time was plotted. From the graph, the minimum corresponds to the total energy associated with the reactants that do not approach each other, and the maximum corresponds to the total energy in a system very close to the transition state. The activation energy is the difference between these two values.
Ea(F+H2) = -103.751-(-103.944) = 0.193 kcal/mol
Ng611 (talk) 15:16, 1 June 2018 (BST) There's still a significant residual gradient here. One alternative would be to run a dynamics simulation (making sure to set internuclear momenta to zero) as this would allow the system to evolve more rapidly.
Ea for the reverse reaction was determined in a similar way: the H-H distance was decreased by 0.01 relative to the transition state and also 100000 steps were selected. The activation energy was determined as the difference between the minimum (corresponding to HF and H that do not interact) and maximum (corresponding to a system near the transition state).
Ea(HF+H) = -103.673-(-133.885) = 30.212 kcal/mol
Note: the kinetic energy, which is not shown in the graphs as they are zoomed in on the potential energy, was zero in both cases.
Release of energy in exothermic reactions
This question was already mostly answered in the Exothermic vs. endothermic reaction section. When a strong bond is formed, certain amount of the energy released during this process can offset the energy required to break the weak bond in the reactants; the excess energy, due to the conservation of energy principle, has to be lost into the surroundings in a certain form, in most cases as heat. Heat can be defined as a rapid movement of particles (rotational, vibrational or translational) so the F+H2 reaction can be expected to generate species that move and/or vibrate more rapidly. This expectation was confirmed when the energy vs. time plot was made for a random set of parameters for a reactive trajectory (r(H-F) = 2.4 Å, r(H-H) = 0.74 Å, p(H-F)= -0.8, p(H-H) = 0.1):
Before the transition state is reached, which corresponds to the time interval t = 0-3, the reactants barely vibrate (low kinetic energy) since the amplitude of the oscillation is very small. However, when the reaction proceeds to the side of the products, the molecules start vibrating much more (the amplitude of the oscillations rapidly increases, higher kinetic energy) so the temperature of the reaction mixture rises (as heat is being generated). This can be experimentally confirmed by calorimetry which studies the flow of heat throughout a reaction by measuring the change in temperature.
Ng611 (talk) 15:18, 1 June 2018 (BST) Correct mechanism of energy release, but unfortunately calorimetry won't help you here as it doesn't distinguish between translational and vibrational kinetic energies.
Polanyi's rules
Polanyi's rules state that reactions with late transitions states are more efficiently promoted by vibrational energy while early transition state reactions are more efficiently promoted by transitional energy.[2] The F + H2 reaction is exothermic so has an early transition state. Therefore, based on the Polanyi's rules, it can be expected that this reaction will be more likely to take place with higher translational energy. This was tested with two sets of parameters:
1.) The distances selected were r(F-H) = 2.4 Å and r(H-H) = 0.74 Å so that the reaction starts at the side of reactants at the bottom of the well. The momentum p(H-H) was set to -2.3 which results in a relatively high vibartional energy while the momentum p(F-H) was kept low at -0.5 which corresponds to a very low translational motion. The resulting trajectory was unreactive:
2.) In this set, the following parameters were selected: r(F-H) = 2.4 Å, r(H-H) = 0.74 Å, p(H-H) = 0.1 (low vibrational energy) and p(H-F) = -0.8 (slight increase in translational energy compared to the first set). These parameters resulted in a reactive trajectory:
These results are in accordance with the Polanyi's rules: in the first set, the translational motion was kept minimal so that the reaction was governed by vibrational energy and it was found that the products were not formed. In the second set, the translational energy was slightly increased while the vibrational energy was decreased dramatically and the resulting trajectory was reactive. This means that the vibrational energy does not have a significant impact on the reaction whereas translational energy affects the reaction significantly as only a small increase could lead the reactants to products. This matched the prediction based on Polanyi's rules.
A similar experiment was done for the reverse reaction which is endothermic, therefore having a late transition state. According to the rules, the exact opposite should be found than in the first experiment. The following sets of parameters were selected:
1.) r(F-H) = 2.4 Å, r(H-H) = 0.74 Å (these distances correspond to the valley floor at the side of the reactants), p(H-H) = -5 (high translational energy) and p(H-F) = -0.4 (low vibrational energy). The trajectory was unreactive:
2.) r(F-H) = 2.4 Å, r(H-H) = 0.74 Å, p(H-H) = -1 (low translational energy) and p(H-F) = -0.8 (small increase in vibrational energy). The trajectory was reactive:
The result shows that the vibrational energy is more important for endothermic reactions: When very high translational energy and low vibrational energy were set, the reaction did not take place but when the vibrational energy was slightly increased while keeping the translational energy relatively low, the products were formed. Therefore, the prediction based on Polanyi's rules was confirmed.
Ng611 (talk) 15:20, 1 June 2018 (BST) Excellent second section and overall an excellent report - well done. Remember to be as precise and unambiguous as possible with your language, to demonstrate that you're in complete command of the subject matter and (more importanly) to avoid confusion for the reader. Besides this, a very well written report!