MRD:als15
Exercise 1: H + H2 System
PES Gradient at Minima and Transition State
The gradient of the PES at minima and the transition state is zero. Maxima (transition state) and minima of a PES, V(x, y), can be distinguished: It is a maximum when (VxxVyy - V2xy) > 0 and Vxx < 0 and Vyy < 0. The point is a minimum when (VxxVyy - V2xy) > 0 and Vxx > 0 and Vyy > 0.
(Where do these equations come from? I don't quite agree with them, especially without explanation. A transition state is not a maximum... it is only a maximum along the reaction coordinate Tam10 (talk) 16:02, 6 June 2017 (BST))
Locating the Transition State
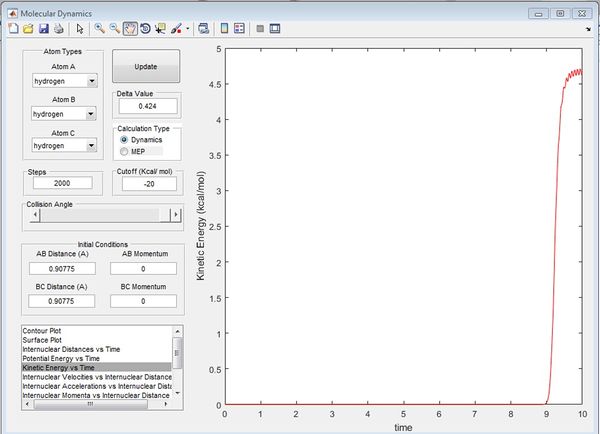
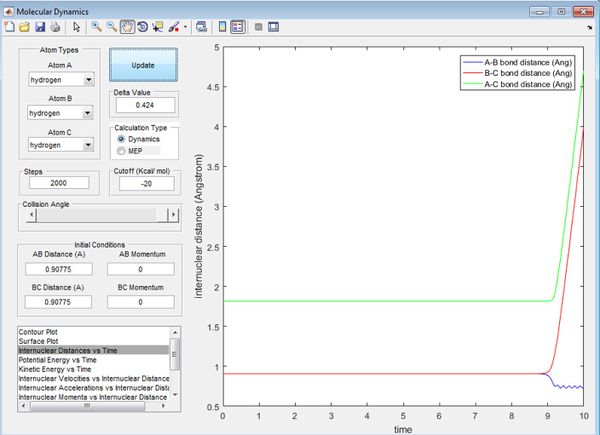
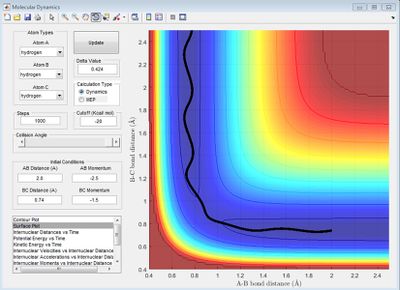
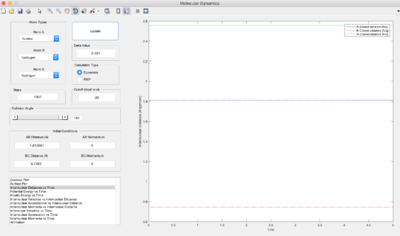
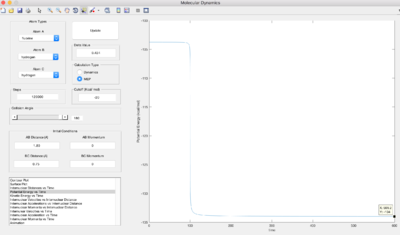
At the transition state, the gradient of the potential is zero, the net force is zero and so the H atoms are stationary and the kinetic energy is zero. If r is shorter or longer than rts, the potential energy would be lower than the maximum value, and therefore kinetic energy will not equal zero. Best estimate of rts=0.90775 Å. The kinetic energy vs. time graph shows that KE=0 for a while, then it increases at t=9.0s. This is because it can never be the exact transition state, where KE=0. The internuclear distance vs. time graph shows there is no movement of the H atoms.
(Not seconds! Tam10 (talk) 16:02, 6 June 2017 (BST))
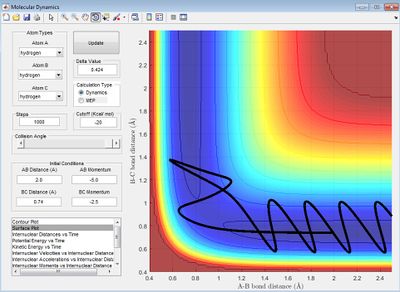
Trajectories from r1 = rts+δ, r2 = rts
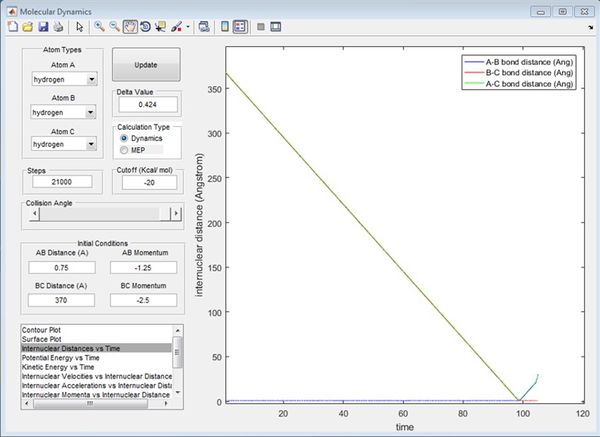
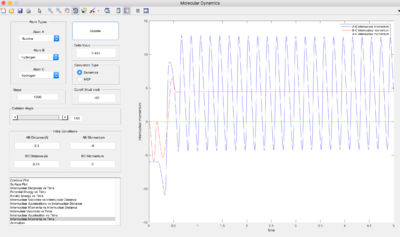
When r1 (BC) = 0.91775 and r2 (AB) = rts, AB becomes shorter, then oscillates and BC increases. The MEP shows no oscillation of the new AB bond, whereas the dynamics does. At t = 100 s, r1 = 370, r2 = 0.75, p1 = 2.5, p2 = 1.25. If instead r1 (BC) = rts and r2 (AB) = 0.91775, at t = 100 s, r1 = 0.75, r2 = 370, p1 = 1.25, p2 = 2.5, which reflects a new BC bond being made as opposed to an AB bond. When the initial conditions are set to the final conditions but with reversed momenta, the internuclear distance-time graph shows r1 (BC) decreases from 370 Å to 0.75 Å and r2 (AB) increases from 0.75 Å, reflecting AB creating a new bond and BC breaking its bond via it transition state where AB=BC.
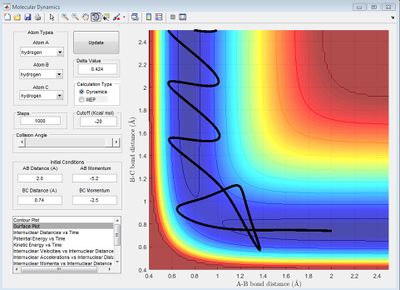
Reactive and Unreactive Trajectories
Transition State Theory1
In the Transition State Theory, the reactants are assumed to be in equilibrium with the activated complex. The activated complex can then become the reactants or the products, but once a product, it will not revert into the activated complex as they are not in equilibrium. The rate of product formation depends on the concentration of the activated complex, the rate at which it decomposes and to what it decomposes into. In TST, if the system has passed the barrier and has formed into product, it is counted as a reactive trajectory. However, this conflicts with scenario five above. Since TST results in over-counting the number of trajectories that are reactive, the rate of reaction predicted by TST would be greater than that measured. The rate predicted by TST is good if the products are unlikely to revert back to reactants, such as when the temperature is low and products are unlikely to have enough energy to overcome the activation energy.
Exercise 2: F-H-H System
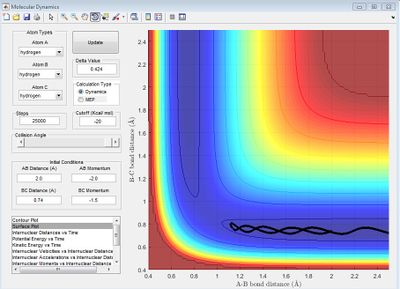
PES Inspection
Locating Transition State
The bond enthalpy for H2 is 436 kJ mol-1 and 569 kJ mol-1 for HF. The reaction F + H2 -> HF + H is exothermic, releasing 133 kJ mol-1 into the surroundings. As the H-F bond is stronger than the H-H bond, more energy was released in bond making than energy needed to be put in for bond breaking.
According to Hammond's Postulate, if the direction F + H2 -> HF + H is exothermic, the energy of the transition state is similar to that of the reactants. The configuration is also going to resemble more the reactants, so the activated complex will have a HH distance close to H-H bond length (0.74 Å) and HF distance will be significantly larger than H-F bond length (0.91 Å). The an estimate for the transition point was located at HF = 1.81 Å, HH = 0.74 Å: It gave a small average kinetic energy of 4 x 10-4 kcal/mol and relatively constant internuclear distances for five seconds, which is a good estimate for a configuration in which the potential energy is at a maximum.
Activation Energy
To find the activation energy for H2 + F -> HF + H, the HF distance was made to be 0.01 Å longer than that at the transition state and the HH distance was made to be 0.01 Å shorter. The activation energy is 0.84 kJ mol-1. To find the activation energy for HF + H -> H2 + F , the HF distance was made to be 0.01 Å shorter than that at the transition state and the HH distance was made to be 0.01 Å longer. The activation energy for this reaction is 126.36 kJ mol-1, which is much greater than the activation energy in the other direction. This agrees with the fact the HF bond is much stronger than the HH bond, and so more energy is needed to get HF from its bond length to its internuclear distance at the transition state.
Reaction Dynamics
F + H2
Conditions (HF =2.3, HH=0.74, p(HF) = -6, p(HH) = 0) were set for a reactive trajectory of F + H2 -> HF + H. The internuclear momenta vs. time graph shows that the new HF bond formed has greater vibrational energy than the old HH bond, and so overall the vibrational energy of the system has increased. As the reaction is exothermic, potential energy decreases and kinetic energy of the system must increase by the same amount to conserve total energy. Through calorimetry, one can measure the increase in kinetic energy in the form heat transferred into the surroundings by measuring the temperature change. However, this would only confirm that the total KE (translational, vibrational and rotational energy) increases, not specifically vibrational energy.
Below, pHH was varied whilst pHF = -0.5, rHH =0.74 and rHF =2.3.
| pHH | Result | Internuclear momentum vs. Time |
|---|---|---|
| 2.6 | Reactive | 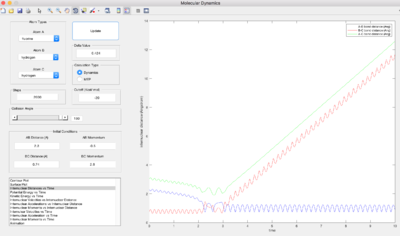 |
| 2.3 | Reactive | 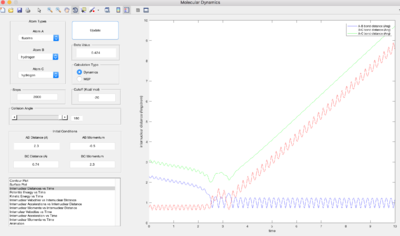 |
| 0.5 | Unreactive | 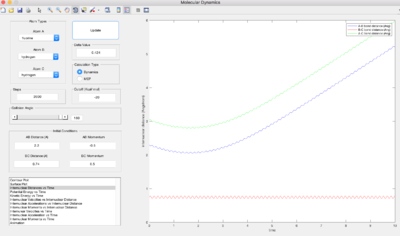 |
| -2.4 | Reactive | 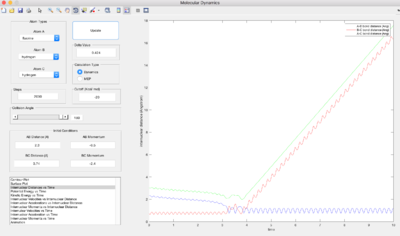 |
| -3 | Unreactive | 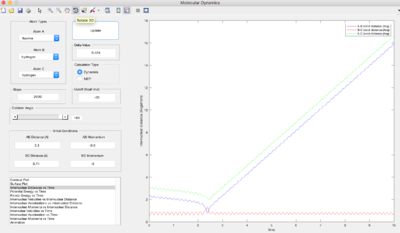 |
When pHH = 0.1, pHF = -0.8, rHH =0.74 and rHF =2.3, the reaction was successful.
 |
H + HF
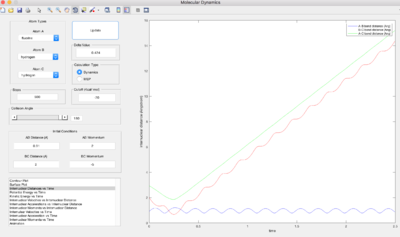 |
 |
Polanyi's empirical rule2 suggests a high vibrational energy makes a reaction with a late transition state (i.e. an endothermic reaction) more efficient, whereas a high translational energy makes a reaction with an early transition state (exothermic reaction) more efficient. For F + H2 -> HF + H, which is exothermic, a range of translational energies (pHH) were tried with a small vibrational energy (pHF). Some were successful, even though Polanyi's rule suggests a high vibrational energy is needed. For the opposite reaction, which is endothermic, it is again true that one can obtain a reactive trajectory with either high translational energy and low vibrational vibrational energy or high vibrational energy and low translational energy, which disagrees with Polanyi's rules. The conditions tested above suggest that if you have high translational energy, you have to have low vibrational energy (or vice versa), i.e. there is a maximum total kinetic energy, otherwise the trajectory recrosses the transition state.
(You've contradicted yourself here - vibrational energy is more decisive in crossing a late transition state. Also remember that you are testing against an empirical rule - real systems explore a huge number of "trajectories" compared to the dozens that we explore here. Tam10 (talk) 16:02, 6 June 2017 (BST))
References
1. Levine, Raphael D., Molecular Reaction Dynamics,Cambridge University Press, 2005, ch.5
2. Theoretical Study of the Validity of the Polanyi Rules for the Late-Barrier Cl + CHD3 Reaction Zhaojun Zhang, Yong Zhou, Dong H. Zhang, Gábor Czakó, and Joel M. Bowman The Journal of Physical Chemistry Letters 2012 3 (23), 3416-3419 DOI: 10.1021/jz301649w