MRD:al7215

H + H₂ system

Dynamics from the transition state region

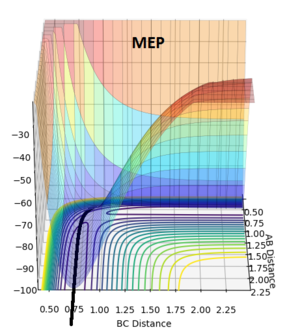
At the minimum and transition structures, both the gradient of the potential energy surface is zero perpendicular to the reaction path, i.e. ∂V/∂s=0 (where s is perpendicular to the reaction path). However, the minima and transition structures can be distinguished by looking at the second derivative of the reaction path. This is as the transition structure is maximum along the reaction path (∂V²/∂r² < 0), whereas the minima is still a minima along the reaction path.

Ng611 (talk) 23:11, 7 June 2018 (BST) This is correct but it's a bit of a confused explanation. A diagram would help here/

Locating the Transition State

Internuclear Distances vs Time plot at estimated transition state position (r_ts= 0.9074).

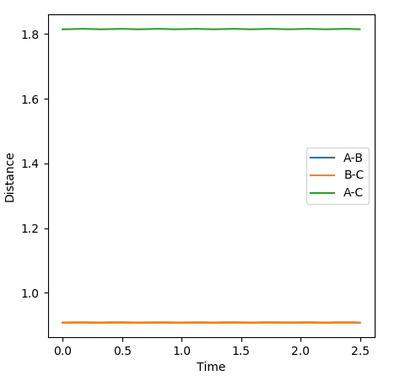
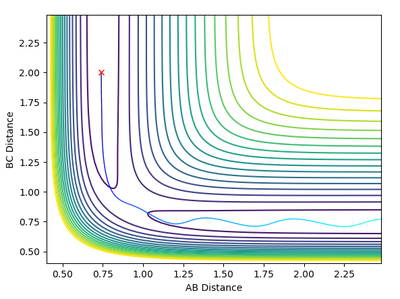
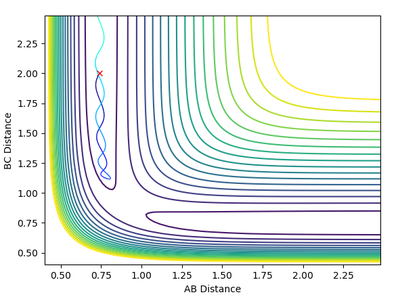
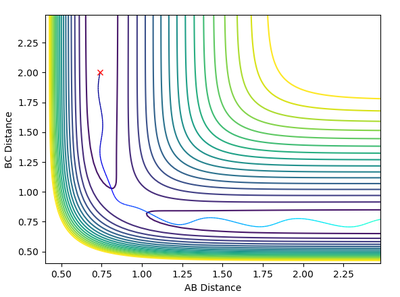
In theory, there will not be any oscillations at the transition state if the trajectory starts off with zero initial momentum since the ridge is flat. Moreover, since we are only estimating the transition state position, we would want to find a position where there are little/ no oscillations. Thus, the best estimate of the transition state position is found to be r_ts= 0.9074 as there exists almost no oscillations (evident from the above Internuclear Distances vs Time plot).

Calculation of Reaction Path using MEP and Dynamics

MEP vs Dynamics
		Minimum Energy Path (MEP) corresponds to the trajectory of minimal energy taken by the reactants as they transition to the products. As the the velocity always resets to zero at every step, MEP will be directed by the gradient of the potential well instead of the velocity of the molecules. It is an ideal trajectory that simply follows the valley floor to the reaction's end state and only allows for translational motion. Conversely, Dynamics reaction path is the actual trajectory taken by the molecules. In this example, there is a deviation of the actual trajectory (dynamics) from MEP as the acceleration after the transition state allows for the actual trajectory to climb up the side of the potential well and have oscillatory motion as well.

Ng611 (talk) 23:12, 7 June 2018 (BST) Good explanation!

Reactive and Unreactive Trajectories

p1	p2	Total Energy	Trajectory	Plot	Description
-1.25	-2.5	-99.018	Reactive		The trajectory starts off at the position marked X. The high momentum of C means that that the translational energy (ET) is high and there is sufficient kinetic motion for motion along BC to overcome the activation barrier, leading to a reactive trajectory. The acceleration after passing the transition state subsequently allows the trajectory to climb to the side of the potential and initiate a B-C vibration.
-1.5	-2.0	-100.455	Unreactive		In comparison to the previous example, this example has a reactant diatomic (AB) with a higher vibrational excitation(EV) but a lower C momentum, thereby lower ET. The translational kinetic energy is unable to overcome the activation barrier, thus making it an unreactive trajectory.
-1.5	-2.5	-98.955	Reactive		Similar to the first example, there is enough translational kinetic energy to surmount the activation barrier and lead to a reactive trajectory. Moreover, a slight difference is that C is now approaching a vibrating AB molecule, instead of a non-vibrating one (as in case 1).
-2.5	-5.0	-84.954	Unreactive		This plot shows a trajectory which passes the transition state and reflects off the potential well, causing it to recross the barrier and return to the reactant channel at a higher vibrational state.
-2.5	-5.2	-83.414	Reactive		This plot also shows a trajectory which undergoes barrier recrossing, transitioning between the reactant and product states. Moreover, the trajectory eventually channels into the product side and at a higher vibrational state.

Main Assumptions of Transition State Theory

The main assumptions of Transition State Theory (TST) are as such:

1. Electronic and nuclear motions can be separated and treated independently, just like the Born-Oppenheimer approximation for wavefunctions in quantum mechanics;

2. Maxwell-Boltzmann distribution determines how the reactant molecules are distributed among the various states;

3. Molecular systems can cross the transition state once, and only in the direction from reactants to products;

4. In the transition state, the translational motion can be treated classically and separated from other motions along the reaction coordinate

Transition State Theory predictions for reaction rate values usually overestimate experimental values. This is as TST assumes that trajectories cannot recross the transition state, but if they do like in some cases, each of such crossing will be treated as an independent trajectory. So for instance, if there are 8 crossings of the saddle point (transition state) in the direction from reactant to products, the theory will count all of them as independent trajectories contributing to the reactive flux. In reality, it might be that only two out of the eight trajectories reached the product side. Thus the rate constant predicted by TST would have been four times larger than the actual rate constant.

Ng611 (talk) 23:14, 7 June 2018 (BST) You've got the right overall picture, but really you have far too few data points to quantify the degree of overestimation.

That being said, assumption 3 is still quite a good approximation for molecular systems dealing with thermal reactants with a barrier that is much higher than the thermal energy. This is as once the barrier has been crossed, it is unlikely that the motion downhill to the products will reverse upon itself. Thus, TST works best at ordinary temperatures when, due to the Boltzmann factor, there is little excess energy available for barrier to be recrossed.

F - H - H system

Potential Energy Surface (PES) Inspection

Energetics and Bond Strength

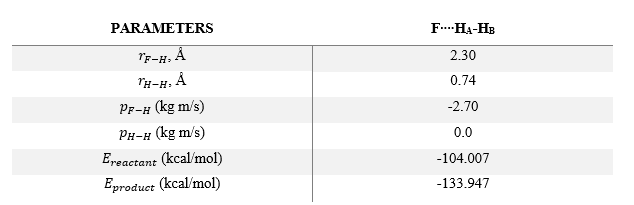
Evident from the table of values and the plot below, it can be noted that F + H₂ is an exothermic reaction. The system moves from a higher energy reactant state to a lower energy product state, releasing about 30 kcal/mol of energy during this transition. This also shows that H-F has a greater bond strength than H-H bond as the energy gained from the formation of one H-F bond more than compensates for the energy lost in breaking one H-H bond. This postulation is supported by literature, with the bond dissociation energies of H-F and H-H bond being 5.869 eV and 4.478 eV respectively.

Correspondingly, H + HF is an endothermic reaction.

Potential Energy Surface of F-H-H system

Locating the Approximate Position of Transition State (TS) using Hammonds' Postulate

Hammond's Postulate states that the transition state will most closely resemble to the reactants or products that has the closest energy to it. For an exothermic reaction, the transition state will resemble the reactants, with the system having an early transition state. Additionally, unlike the H + H₂ system previously considered, the PES of F + H₂ system is highly asymmetric, so r_H-F is not equal to r_H-H at the transition state, but will be largely different. After testing out some initial conditions (in particular varying r_H-F in the region of 1.7-2.3 as the reaction has an early TS), the approximate position of transition state is as follows: r_H-H= 0.7448 and r_H-F= 1.8108. These values can be validated by looking at the following Internuclear Distances vs Time Plot and observing that r_H-F (blue line) and r_H-H (orange line) are constant (i.e. there are no oscillations and the the three atoms are stationary)

Internuclear Distances vs Time plot at approximate transition state position (Dynamics: 1000 steps)

Activation Energy of Forward and Backward reactions

Activation Energy Calculations using MEP

The activation energy (E_a) of the forward (F + H₂) and backward reaction (H + HF) can be calculated using MEP. Generally, this is done by slightly perturbing the system slightly to the left or right from the approximate transition state position so that the trajectory will follow the path of minimal energy and ultimately reach the valley floor of the reactant or product after a sufficient number of MEP steps. The energy at t=0 is the energy of the transition state while the energy at the very end is the energy of either the reactants or products state. Activation energy is thus the energy gap between energy at t=0 and t=N (where N is the time in which the last MEP step is completed). From the two plots, it can be noted that E_a= 0.255 kcal/mol for F + H₂ reaction and E_a= 30.194 kcal/mol for H + HF reaction. MEP of the H + HF reaction was calculated using 100,000 steps, but in reality, much less steps is needed as the product floor is reached slightly after 100s. In contrast, the F + H₂ reaction took about 500,000 MEP steps to reach the reactant valley floor, and even then, the valley floor obtained is not entirely flat. The reason for this is that the trajectory followed a very gentle gradient due to the closeness in energy between the transition state and reactant states.

Ng611 (talk) 23:15, 7 June 2018 (BST) Excellent!

Reaction Dynamics

Mechanism of release of Reaction energy

One set of parameters that lead to a reactive trajectory in a F + H₂ reaction

Plots of a Reactive Trajectory

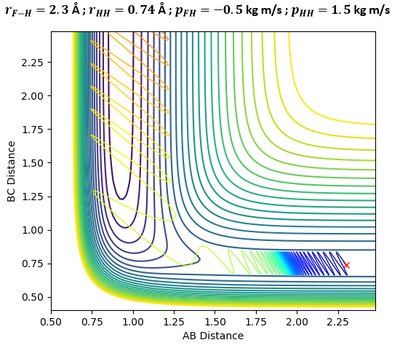
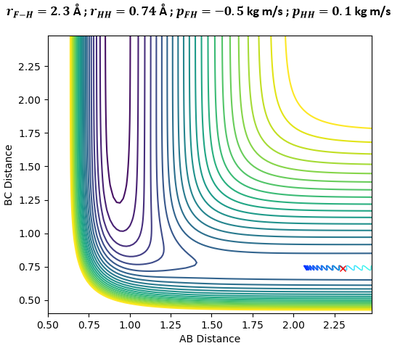
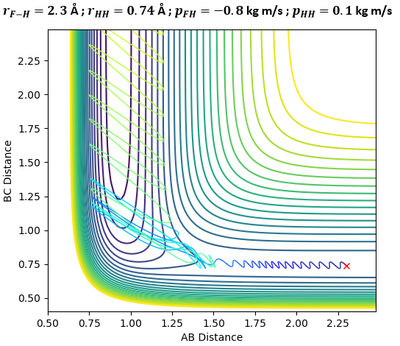
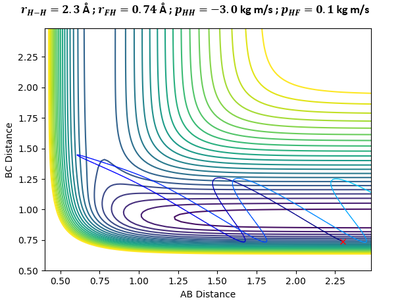
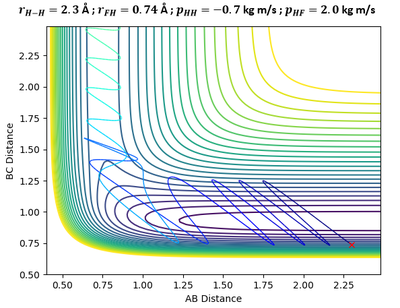
In the above plots, A is the Fluorine atom while BC is H₂ molecule. The mechanism of release of reaction energy is as such: Fluorine, possessing translational kinetic energy, approaches a largely non-vibrating H₂ molecule. Upon collision and after several barrier recrossings at the transition state, the new HF molecule emerges at a vibrationally excited state with some vibrational energy. This can be seen from the large sinusoidal oscillations of HF molecule in the Inter-Nuclear Momenta vs Time plot. Due to the conservation of energy, the gain in vibrational energy of HF molecule means a loss in translational energy of the departing H atom. Thus, H atom absorbs the remainder energy and moves away from HF molecule through a purely translational motion.

Infrared Chemiluminescence is one analytical method that can help to experimentally verify whether the resultant HF molecule is indeed in a vibrationally excited state. If the excitation of HF is primarily vibrational, its radiation will appear in the infrared region of the spectrum between 3 to 15 µm. This technique has been widely used for hydrogen-halogen reactions, producing HX molecules in excited (v, J) states.

Ng611 (talk) 23:16, 7 June 2018 (BST) Excellent suggestion!

Polanyi Empirical Rules

After carrying out an extensive series of calculations on potential surfaces, Polanyi identified the position of transition state as key to understanding the efficiency of the reaction as well as the energy distribution of its reaction products. Polanyi's celebrated set of rules can be summarised as follows:

Efficiency of reaction

Translational energy is most effective for a reaction which has an "early" transition state near the entrance channel, whereas reactant vibrational energy that is far in excess of the barrier height may be ineffective for the reaction. Conversely, a "late" barrier is best surmounted by vibrational rather than translational energy in the reactants.

Energy distribution of products

An "early" transition state generally favours vibrational excitation of the product while a "late" transition state tends to lead to a low product vibrational excitation.

We will now explore how Polanyi's empirical rules can be applied to the following plots shown below:

Plots for F + H2 reaction with varying initial conditions	Description
	This plot shows a set of initial conditions that lead to a reactive trajectory. The high vibrational energy of the diatomic H2 molecule causes it to rattle from side to side near the entrance channel, but still manages to have enough energy to surmount the barrier.
	Conversely, this plot shows a case where having too high vibrational energy in H2 molecule leads to an unreactive trajectory. Polanyi rules predicted that having a reactant vibrational energy far in excess of the barrier height may be ineffective for reaction, but this plot goes a step further to show that the high vibrational energy actually becomes counterproductive and detrimental to achieving a reactive trajectory. The H2 molecule, which starts off with rapid rHH motion, eventually slams into the inner repulsive potential surface wall and bounce back into the entrance channel.
	In comparison to the first two sets of initial conditions, the momentum of H2 molecule is now greatly reduced (i.e. H2 only has a small vibrational energy). The plot thus shows that the reactant translational energy is unable to surmount the barrier, leading to an unreactive trajectory. This is in agreement with Polanyi rules as translational energy is most effective for a reaction with an "early" transition state, and not having enough translational energy will ultimately lead to an unreactive trajectory.
	The initial conditions of this plot is similar to plot 3, just with the momentum of Fluorine atom slightly increased. The system now possesses sufficient reactant translational energy to overcome the activation barrier, leading to a reactive trajectory.

Plots for H + HF reaction with varying initial conditions	Description
	Since H + HF is the reverse reaction of F + H2, it is endothermic and has a "late" transition state. Thus, according to Polanyi rules, a higher vibrational rather than translational energy would be more effective in surmounting the "late" barrier. This plot supports the empirical rules as although the approaching H atom has a high translational energy, because of the low vibration energy of HF, the barrier ultimately could not be surmounted and this led to an unreactive trajectory.
	This plot shows an ideal set of conditions which follows Polanyi rules and leads to a reactive trajectory. The conditions involve having a high HF momentum (i.e. high vibrational energy) and a relatively low momentum for the approaching H atom (i.e. low translational energy).

Ng611 (talk) 23:18, 7 June 2018 (BST) This is an absolutely fantastic report, particularly the second section. You should be very proud of this piece of work!