Molecular reaction dynamics

EXERCISE 1: H + H₂ system

On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?

The transition state is a saddle point which is defined as the point which is both a minimum along one vector and a maximum along an orthogonal vector. Along the reaction path, the transition state is a maximum and along the second vector, which is perpendicular to our initial vector it is a minimum. This can be visualised in the diagram below.

For a co linear system, as given for the H + H₂ system there are two orthogonal degrees of freedom with the coordinates given as follows:

Z = r₂+ r₁

$\frac{\partial V}{\partial Z} = 0$ , $\frac{\partial^{2} V}{\partial Z^{2}} > 0$

S = r₂ - r₁

$\frac{\partial V}{\partial S} = 0$ , $\frac{\partial^{2} V}{\partial S^{2}} < 0$

Note that these are the orthogonal vectors.

The saddle point has the configuration in which r₁ = r₂=r₀and this will be the point at which these two lines intersect on the PES. This is the transition state. S is the tangent to the reaction pathway at the maximum whilst Z bisects the reaction pathway at the same point, but will be seen as a minimum. Correct, but you should mention that r1 and r2 being equal and therefore your definitions of the vectors are specific to the H+H->H2 system. Pu12 (talk) 23:06, 30 May 2019 (BST)

How does the TS compare to a local minimum?. Pu12 (talk) 23:06, 30 May 2019 (BST)

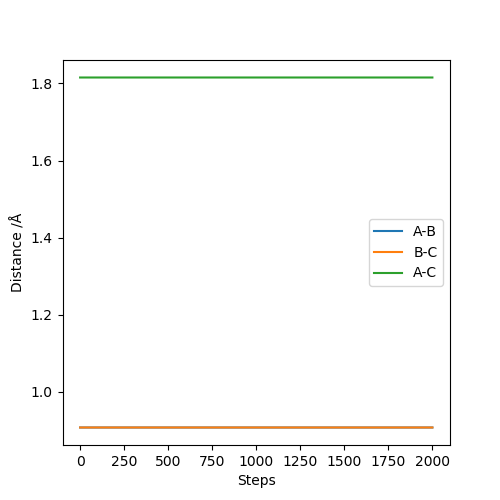
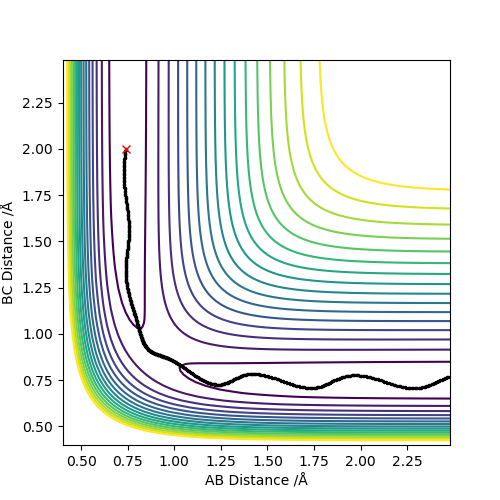
Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

The best estimate was AB = 0.9077425 and BC = 0.9077425. There are only two lines when looking at internuclear distances vs time as seen below. This indicates that two lines are at the same distance and one is covering the other.

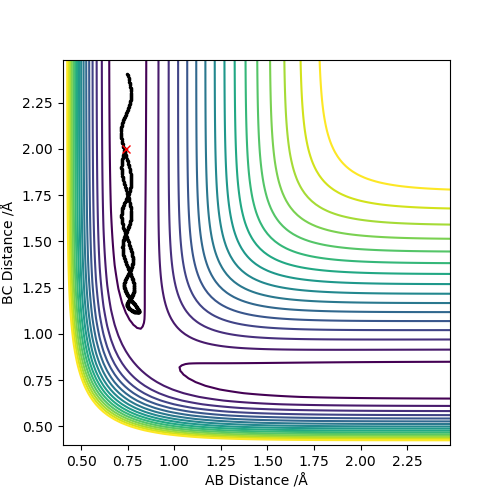
To locate the transition state, is to begin the reaction trajectories close to the transition state. Due to the transition state being a global maxima, the trajectories will either form the reactants or products in order to find the lowest energy configuration. Whether the product or reactants are formed is directly influenced by the trajectories. If the trajectories are closer to the reactants then the reactants will form and if they are closer to the products then the products will form.

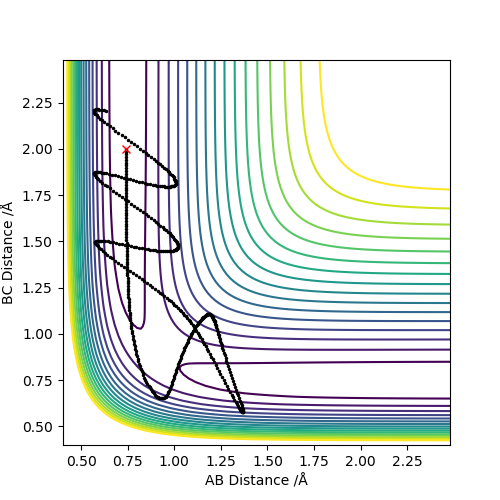
Comment on how the mep and the trajectory you just calculated differ.

Trajectories from r₁ = r_ts+δ, r₂ = r_ts

Along the mep, because the atoms are moving infinitely slowly and the momenta and the velocities always reset to zero, there is no oscillation and hence no vibration. This is seen along the mep where there is no wavy lines. In contrast, when looking at the dynamics, there is oscillation as post collision there is transfer of kinetic energy that causes the molecule to vibrate.
A surface or contour plot would help to illustrate this. Pu12 (talk) 23:06, 30 May 2019 (BST)

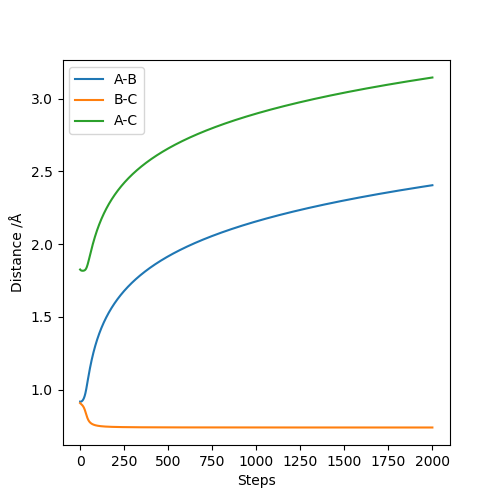
When considering the inter nuclear distance vs time, A-C and A-B distances increase rapidly over the first 250 steps after which the rate of increase of the distance begins to decrease. As the number of steps increases the rate of increase of distance begins to plateau as the gradient flattens. This can be rationalised when looking at the animation where post collision, the molecules initially rapidly move away from one another but the speed at which they move away from each other falls off with time. When considering the dynamic situation, A-C and A-B distances increase at a constant gradient over the course of the plot. The reasoning is that in the dynamic situation, the velocities and momenta are not reset to zero at each step.

It's not necessary to discuss this. Pu12 (talk) 23:06, 30 May 2019 (BST)

You should label your diagrams. Pu12 (talk) 23:06, 30 May 2019 (BST)

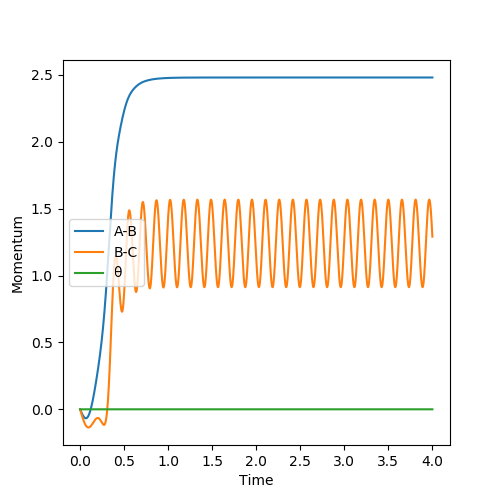
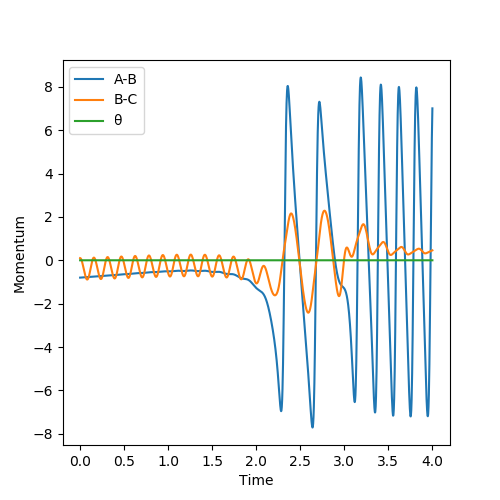
For the same reason as stated as above, the momenta and velocities are reset to zero at each point this means that the momentum vs time plot is a straight line for the mep . However, when running the dynamic situation we see an initial sharp increase in the momentum followed by a constant oscillation of momentum that is due to the momentum being retained within the vibrational modes. For A-B, there is a sharp increase in the momentum which plateaus at the same instance as B-C begins to undergo constant oscillation. This is because A-B refers to the momentum of the system A-B. Once both reach constant momentum the combined system now has a set defined level of momentum with no way to lose it.

Trajectories from r₁ = r_ts, r₂ = r_{ts +δ}

The result of switching the distances is that

Take note of the final values of the positions r₁(t) r₂(t) and p₁(t) p₂(t) for your trajectory for large enough t.

Setup a calculation where the initial positions correspond to the final positions of the trajectory you calculated above, the same final momenta values but with their signs reversed.

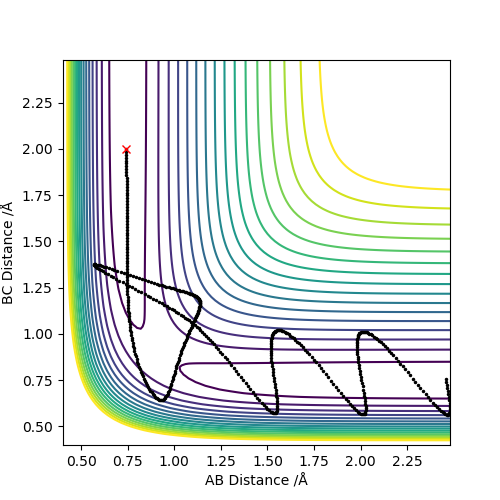
Reactive and unreactive trajectories

p₁	p₂	E_tot	Reactive?	Description of the dynamics
-1.25	-2.5	-99.018	Yes	Reaction proceeds with minimal vibration
-1.5	-2.0	-100.456	No	P₂does not have enough momentum to reach P₁
-1.5	-2.5	-98.956	Yes	Transfer of vibrational energy
-2.5	-5.0	-84.956	No	Product forms but contains too much vibrational energy so dissociates
-2.5	-5.2	-83.416	Yes	Reaction does occur but recrosses the transition state barrier

This descriptions are too vague. You should talk about vibrational energy changes for each one, and mention crossing/recrossing the transition state more. Pu12 (talk) 23:06, 30 May 2019 (BST)

The fact that the last experiment recrosses the transition state barrier is evidence of the breakdown of Transition State Theory, which is presented below. this states that once products are formed, the system cannot travel back through the transition state to the reactants. Good. Pu12 (talk) 23:06, 30 May 2019 (BST)

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

There are two basic assumptions for Transition State Theory, the two most basic are the separation of the electronic and nuclear motions which is the same as the Born-Oppenheimer approximation from quantum mechanics. The second basic assumption is that the reactant molecules are distributed among their states in accordance with the Maxwell-Boltzmann distribution.

There are however, additional assumptions and they are as follows:

Molecular systems that have crossed the transition state in the direction of the products cannot turn around and reform reactants.
In the transition state, motion along the reaction coordinate may be separated from the other motions and be treated classically as a translation.
Even in the absence of an equilibrium between the reactant and product molecules, the transition states that are become products are distributed among their states according to the Maxwell-Boltzmann laws.

You should reference here. Pu12 (talk) 23:06, 30 May 2019 (BST)

Given that Transition State theory neglects quantum mechanical contributions such as influence on and between between electronic and nuclear motions and the idea that molecules passing through the transition state through to the products cannot pass back through to the reactants, this would suggest that there would be deviation between experimental and calculated values using Transition State theory. Would these deviations cause an increase or decrease in rate values? Pu12 (talk) 23:06, 30 May 2019 (BST)

EXERCISE 2: F - H - H system

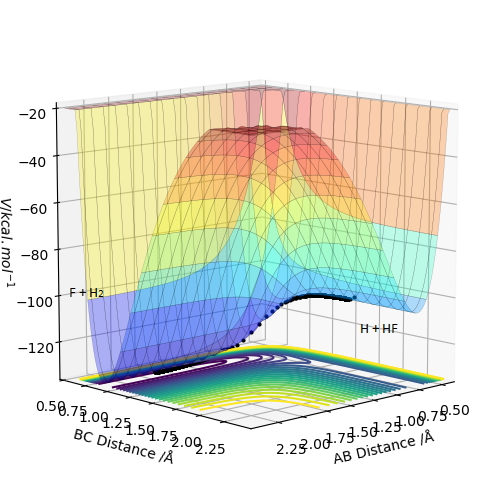
By inspecting the potential energy surfaces, classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

Looking at the PES of F + H₂this indicated the reaction is exothermic because there is a decrease in the energy going from the reactants to products. This can be seen along the reaction path for this reaction where there is a dip in energy on the path to the formation of the products. This makes intuitive sense as the driving force of the reaction will be the formation of a strong F-H (565 Kj/mol) bond, in place of a weaker H-H (464 Kj/mol) bond. Additional evidence that the reaction is exothermic is that when a mep calculation was run with R_AB = 1.812 and R_BC = 0.74 with zero momentum for each case, the reaction proceeded and the products formed with no additional input of energy.

For the H + HF reaction, the reaction is surmised to be endothermic due to as there is no decrease in energy on forming the products. This is in line with intuition considering the strength of the H-F bond. The very high electronegativity of fluorine would make it so that significant energy input would be required to cause this reaction to proceed. This can be seen in the pes below for the H + Hf system where there is a difference in height corresponding to the energies of the reactants and products. Diagrams of the PES would help here, you've put some later on but they aren't labelled and its unclear that they relate to this question. Pu12 (talk) 23:06, 30 May 2019 (BST)

Locate the approximate position of the transition state.

Reaction	r_AB	r_BC	Activation Energy/ Kj/mol Should be kcal/mol Pu12 (talk) 23:06, 30 May 2019 (BST)
F + H₂	1.8108757	0.7448759	0.2673
H + HF	0.7448756	1.8108759	30.251

The positions of the transition states were located through experimentation of the initial AB and BC distances, until the forces acting along AB and BC were zero. The reasoning behind this comes from the notion that

$F = - \frac{\partial V}{\partial r}$

where F is the force If you are discussing force you should include a diagram demonstrating this. Pu12 (talk) 23:06, 30 May 2019 (BST)

and seeing as we are at a saddle point, $\frac{\partial V}{\partial r} = 0$ and hence

$F = 0$

In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.

The set of reaction conditions that were used were:

Atom A: F

Atom B: H

Atom C: H

Distance AB: 2.25

Distance BC: 0.74

Momentum AB = -0.8

Momentum BC = 0.1

These conditions yielded a set of successful reactions, and post reaction and upon formation of F-H, there is transfer of energy in the form of kinetic energy to both the Hydrogen that is travelling away from the reaction complex and also kinetic energy in the bond vibration of F-H. This can be visualised in the Momenta vs Time graph below. Monitoring the emission spectrum of the product and observing electromagnetic radiation in the IR region would allow identification of the product. Correct, calorimetry could also be used as the vibration would be picked up as heat, this likely be easier. Pu12 (talk) 23:06, 30 May 2019 (BST)

For r_BC = 0.74, with a momentum p_AB = -0.5, and several values of p_BC in the range -3 to 3 were explored. For p_BC= -3, the reaction did proceed and there was significant transfer of kinetic energy to the product F-H. What is interesting to note is that the F-H bond forms twice. On the first formation, the bond breaks due to what is assumed to be, too high a vibrational energy. This leads to the reformation of the H-H bond, upon which there is still significant vibrational energy and combined with the electronegativity of the F atom causes the H-H bond to break and the F-H bond to form for the second time. The F-H bond is now stable, although still containing significant vibrational energy. For p_BC= 3, the same phenomena occurs as for p_BC= -3.

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

A transition state for an attractive potential energy surface occurs early in the reaction coordinate and involves high translational kinetic energy (evidenced by the random motion for the reactants) and results in a vibrationally excited product. This translational energy runs up the side of the valley and falls from side to side, showing that there is significant vibrational motion. We can therefore conclude that reactions with attractive potential energy surfaces proceed more efficiently if the energy is in relative translational motion.

In contrast, reactions with repulsive potential surfaces experience a late transition state and are expected to proceed with greater efficiency if the excess energy is present as vibrations. The energy is in the vibration of the reactant molecule and the motion causes the trajectory to move from side to side up the valley as it approaches the transition state. This energy is enough to tip the reactant molecules through the transition state and into the products, it is therefore apparent that the vibrational energy on the repulsive potential energy surface is key to the reactivity and formation of the products.