MRD:ad5215

Exercise 1

What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

The gradient (first derivative) of the surface will be zero at a minimum and at a transition structure (i.e. a saddle point). To distinguish between these points we must look at the second derivative test discriminant, D.

D = f_xx + f_yy - f_xy²

A minimum is defined by D>0 and f_xx>0. A saddle point (transition structure) is defined by D<0.

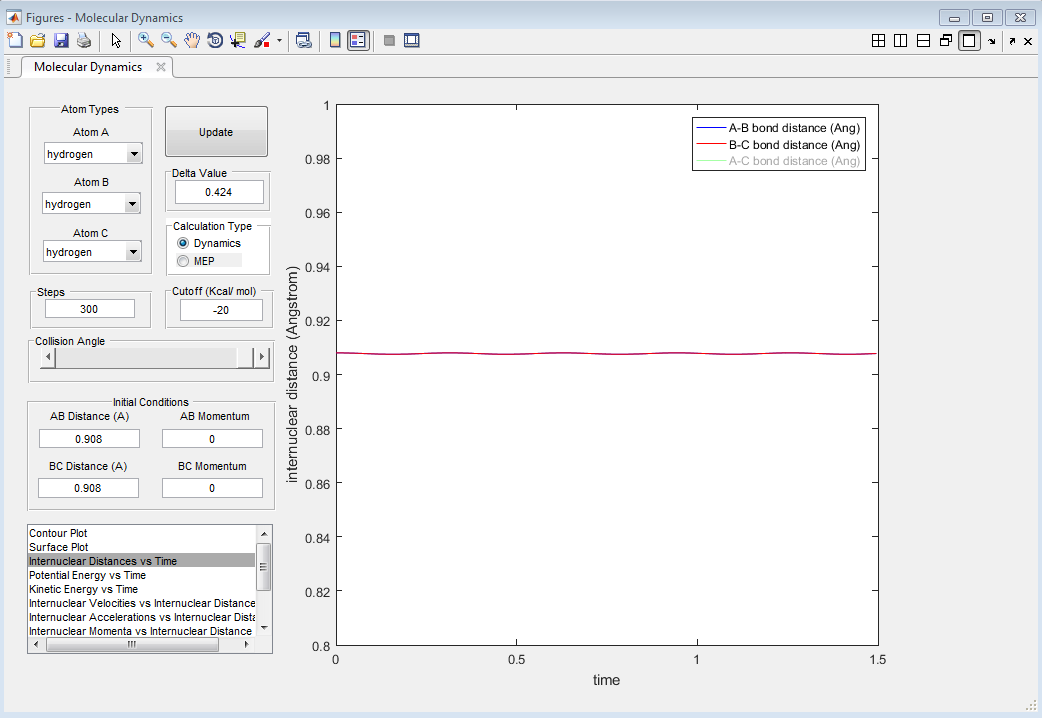
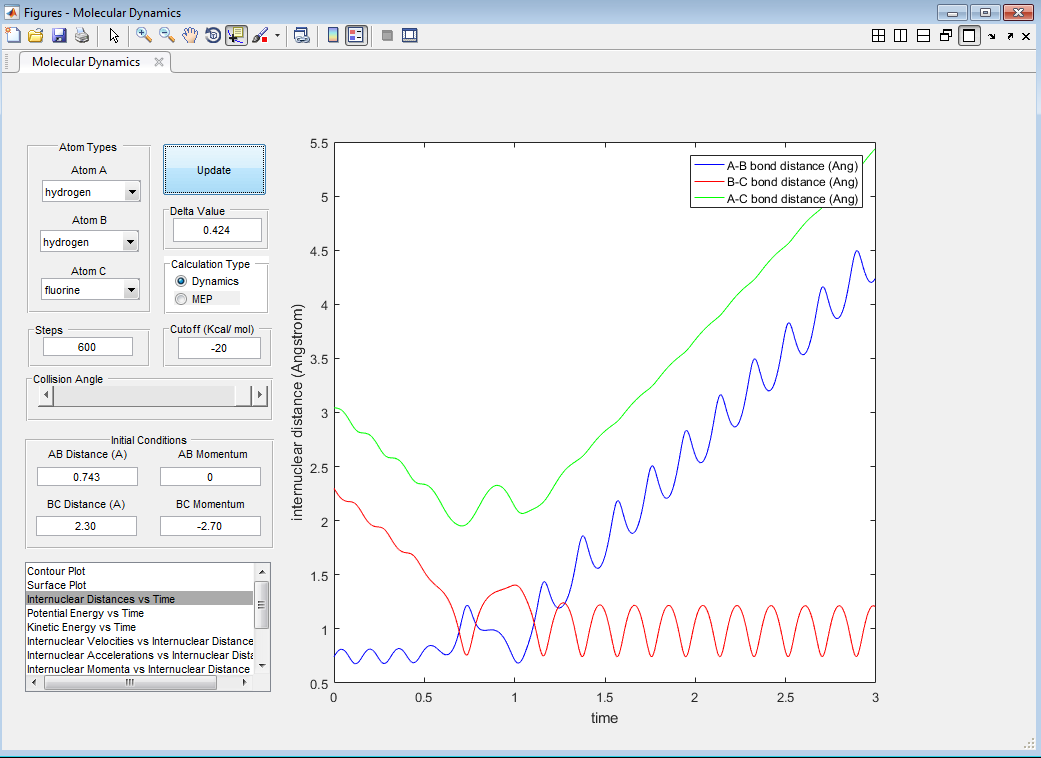
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.

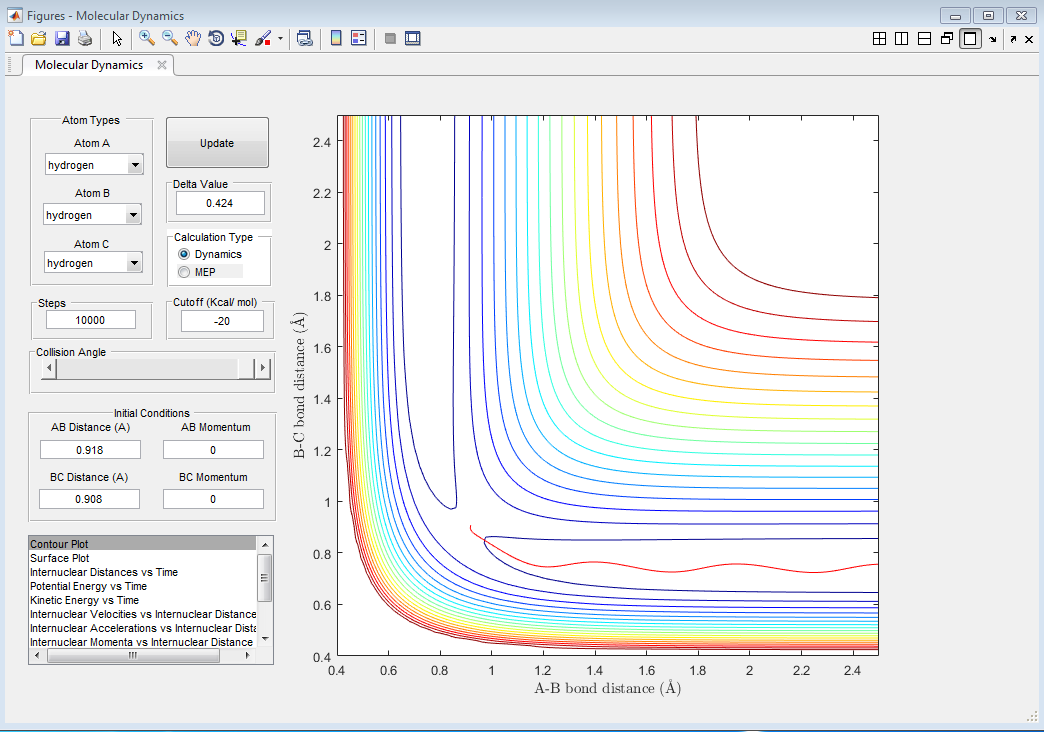
Using the program, it was found that r_ts=0.908 Å. This is the distance where no oscillations (or almost none) are observed; the internuclear distances are constant with time, as shown in Figure 1. Pinpointing an exact value is difficult as a very high accuracy is needed.

Figure 1: A plot of the internuclear distances vs time in the transition state

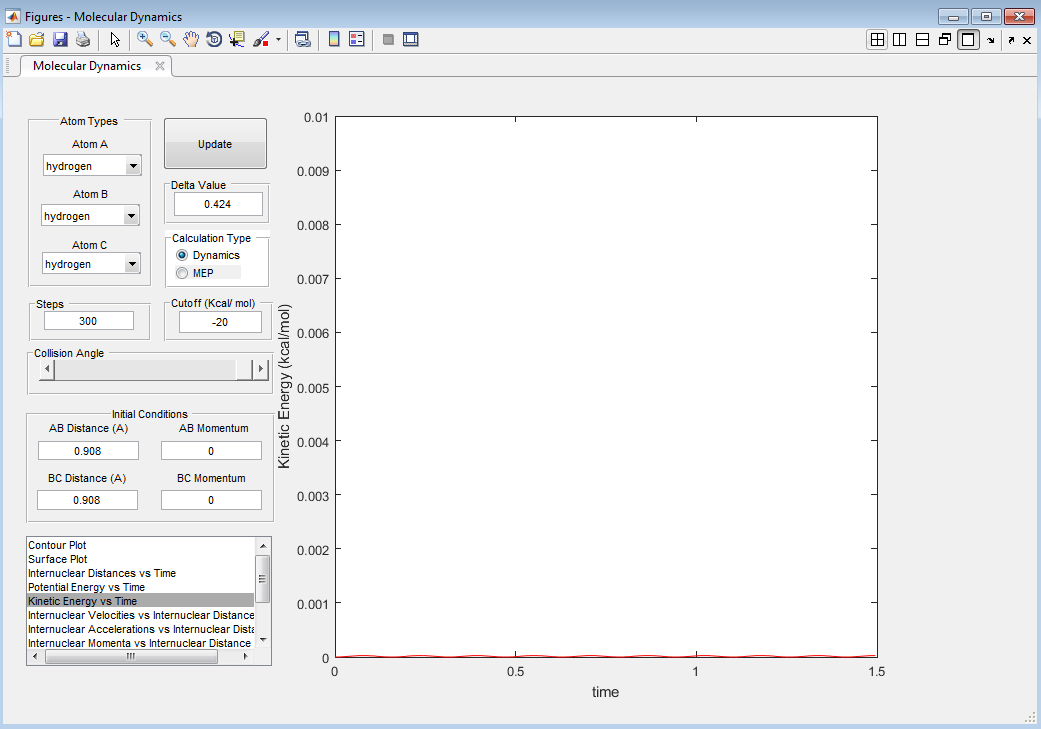
This is the lowest energy point corresponding to equal r1 and r2 values. It signifies that the transition state has no kinetic energy (is static) and only has potential energy (as can be seen from Figure 2).

Figure 2: A plot of the kintetic energy of the transition state vs time

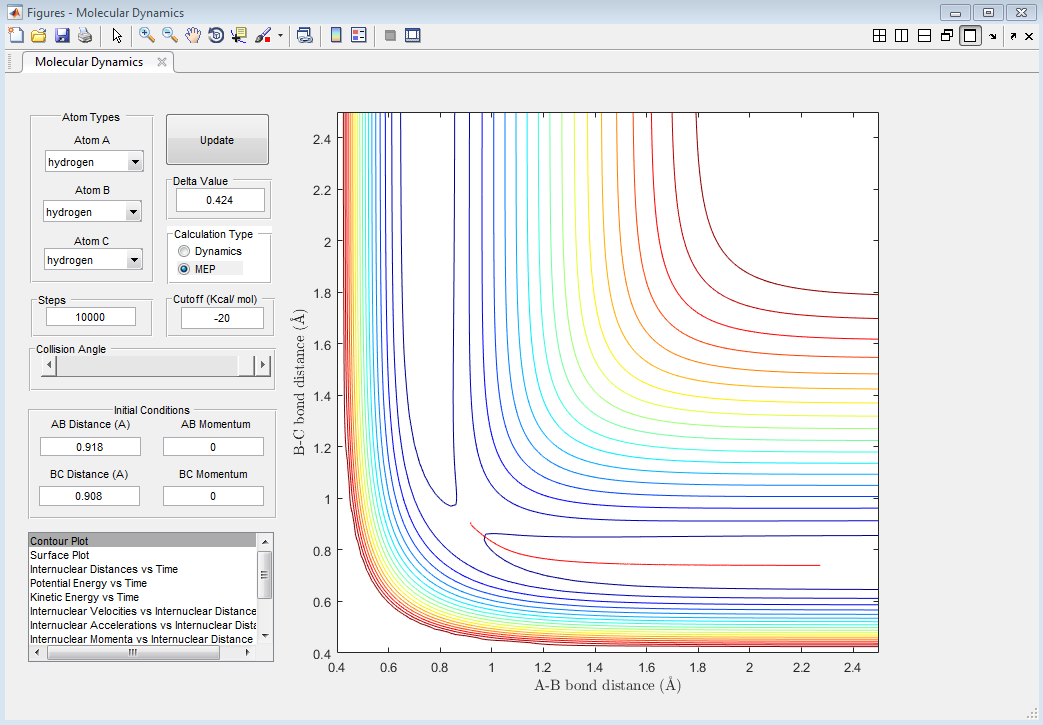
Comment on how the mep and the trajectory you just calculated differ.

The MEP shows the lowest energy path, i.e. one with no oscillatory movement. The dynamic model, which is closer to reality, does show oscillations (as can be seen from the wavy trajectory). Contour plots of these are reproduced in Figure 3 and Figure 4 respectively.

Nf710 (talk) 10:31, 26 May 2017 (BST) MEP start each step with zero momentum

Figure 3: Contour plot of MEP trajectory near transition state

Figure 4: Contour plot of dynamic trajectory near transition state

What would change if we used the initial conditions r1 = rts and r2 = rts+0.01 instead? The new conditions would shift the transition state towards reactants, so the trajectory would now lead to the initial state (molecule AB and free particle C).

Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.

Trial	p1	p2	Reactivity
1	-1.25	-2.5	reactive
2	-1.5	-2.0	unreactive
3	-1.5	-2.5	reactive
4	-2.5	-5.0	unreactive
5	-2.5	-5.2	reactive

• 
  Figure 5: Contour plot, trial 1
• 
  Figure 6: Contour plot, trial 2
• 
  Figure 7: Contour plot, trial 3
• 
  Figure 8: Contour plot, trial 4
• 
  Figure 9: Contour plot, trial 5

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

Transition State Theory

1. Assumes that nuclei are large enough (in comparison to electrons) that they behave according to classical mechanics. Thus, it does not take tunneling into account and assumes that the only way a reaction can occur is if the particles collide with enough "force" (i.e. have enough energy to surpass the activation energy barrier).

2. Assumes that the system will pass over the lowest energy saddle point for any reaction. However, this does not hold at high temperatures; higher energy activated complexes / transition states can be formed.

The first assumption leads to a predicted rate which is, in fact, slower than reality; this is because reactions can proceed via a tunneling mechanism, which increases the probability of the reaction happening and thus the rate. The last assumption predicts a rate faster than the real one, because there is a greater energy barrier to be crossed.

Exercise 2

PES Inspection

Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

F + H₂

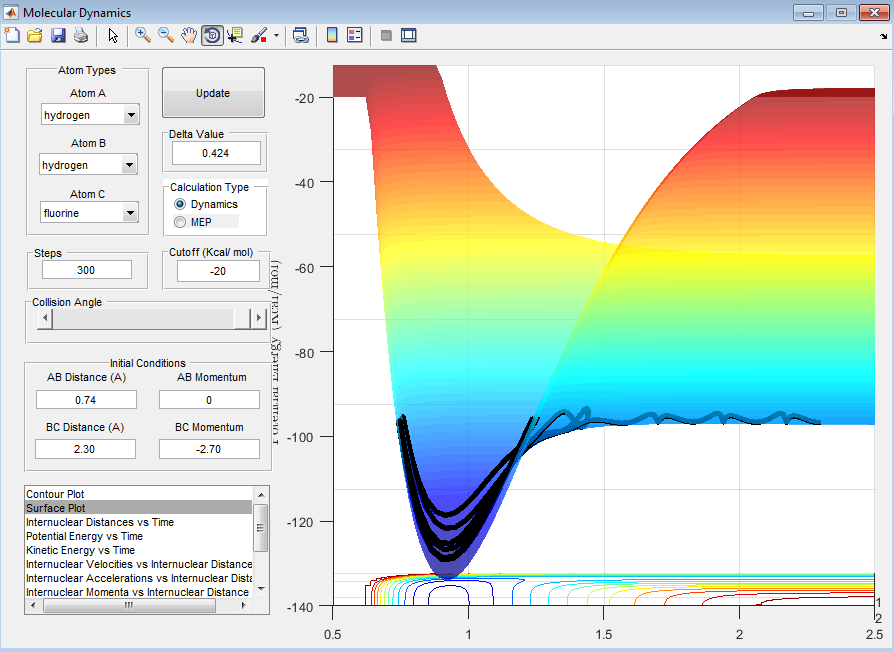
The reaction is exothermic (Figure 10).

Figure 10: Surface plot of F + H₂ reaction

FH + H

The reaction is endothermic (Figure 11).

Figure 11: Surface plot of HF + H reaction

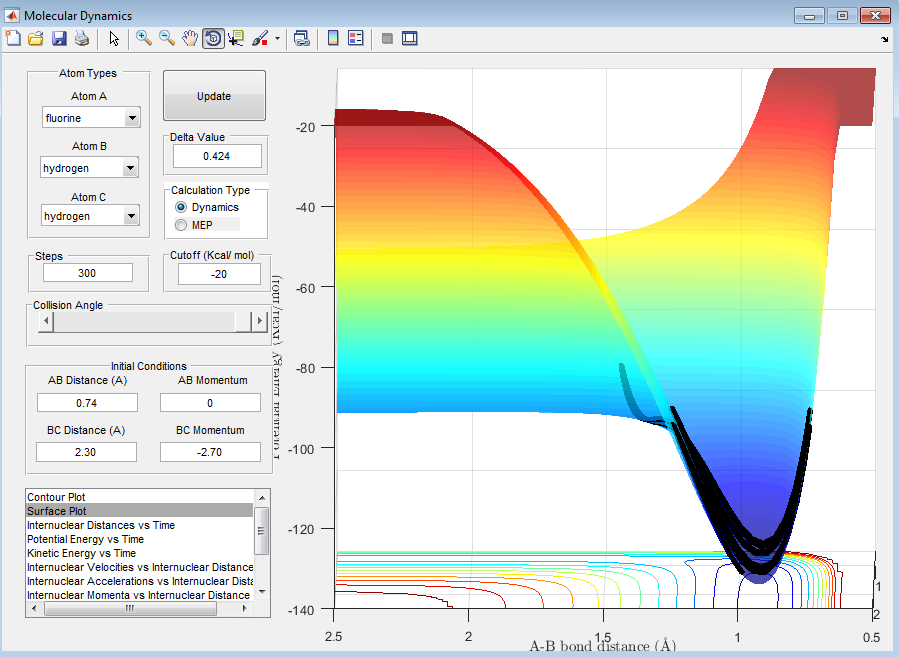
This agrees with theory, as the H-F bond is much stronger than the H-H bond, as it has more ionic character (due to the high electronegativity of F). Therefore, breaking the H-F bond requires energy, leading to an endothermic reaction.

Locate the approximate position of the transition state.

According to the Hammond postulate, the transition state will resemble the state to which it is closest in energy (reactants or products).

In the case of the F + H₂ collision, the reaction is exothermic, and therefore the transition state will resemble the reactants, i.e. the F + H₂ system. In the case of the FH + H collision, the reaction is endothermic and therefore the transition state will resemble the products, i.e. the F + H₂ system.

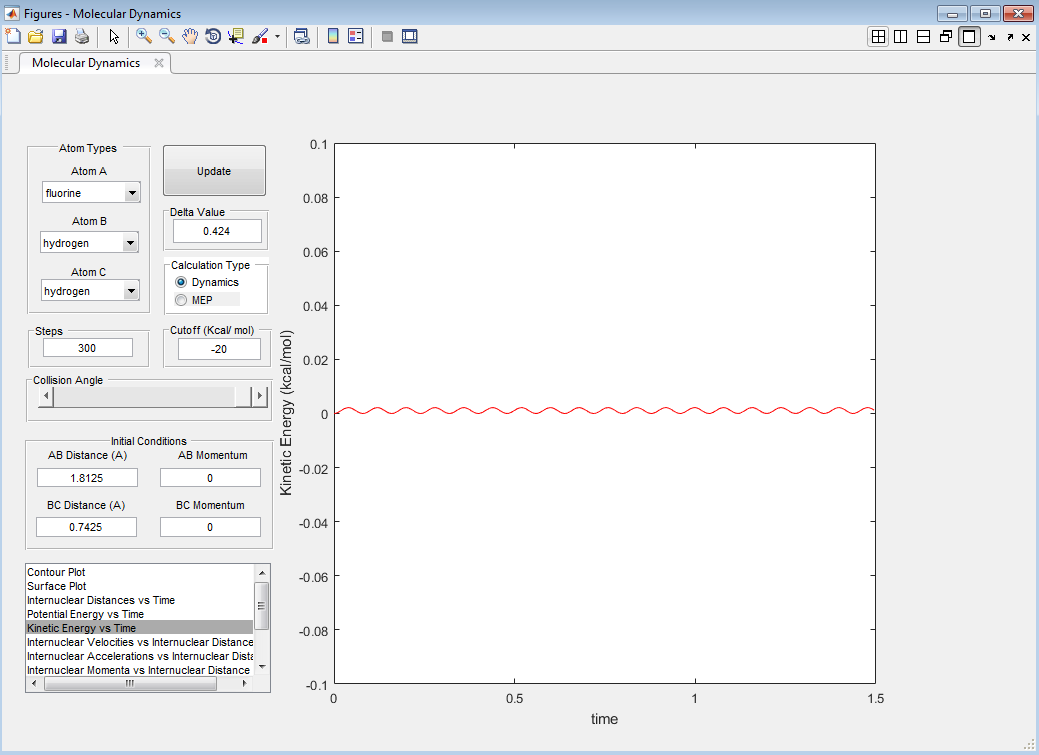
The transition state was found to be a system with an H-H bond length of 0.743 Å and an H-F bond length of 1.813 Å. It has a minimum kinetic energy (close to 0) given in Figure 12 and is represented as a point on the potential energy surface.

Figure 12: Plot of the kinetic energy of the transition state vs time

Report the activation energy for both reactions. The activation energies for the forward exothermic reaction and the backward endothermic reaction were found by subtracting the potential energies of their respective reactants.

State	Potential Energy/ kcal mol-1	Activation energy / kcal mol-1
Transition state	-103.75	n/a
F + H2	-104.02	0.37
FH + H	-134.03	30.28

Reaction Dynamics

In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

The energy released in the exothermic reaction is converted from potential energy to kinetic energy. The "free" atom will gain energy and have a greater velocity than the F atom. The new molecule will oscillate faster and more vigorously (greater amplitude of oscillations), even though it has a greater reduced mass than the H₂ molecule. This can be seen in Figures 13 and 14.

Figure 13: Plot of internuclear distances vs time

Figure 14: Plot of internuclear velocities vs time

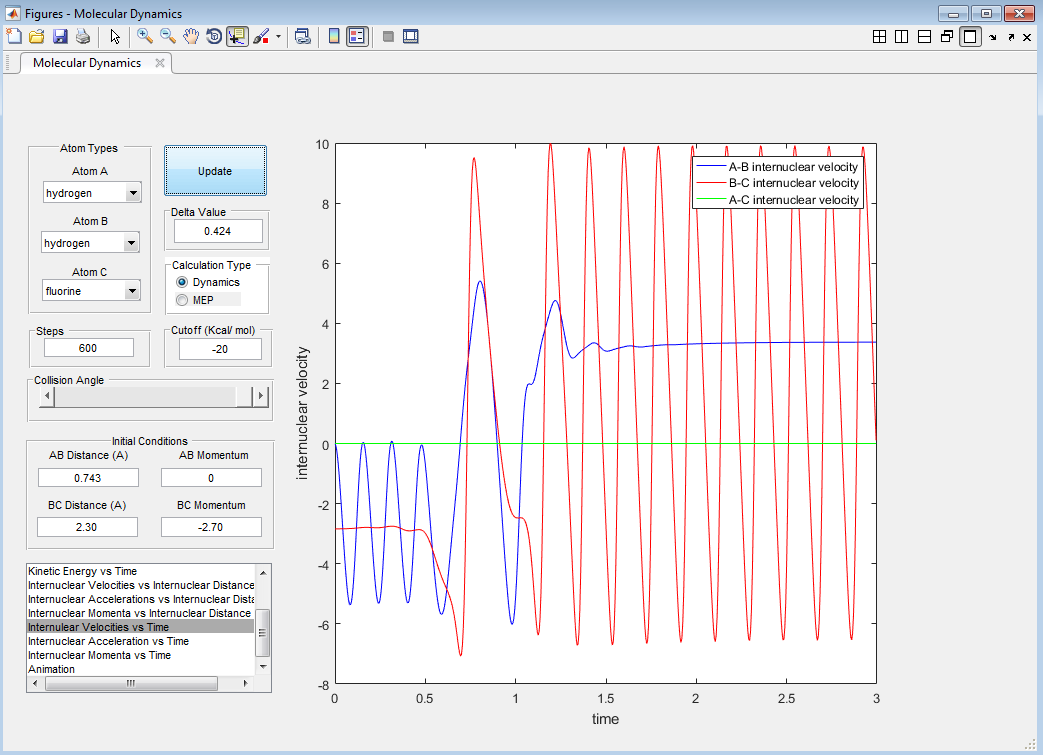
Discuss how the distribution of energy between different modes (translation and vibration) affects the efficiency of the reaction, and how this is influenced by the position of the transition state.

According to Polanyi's rules, the effect of the energy distribution depends on the relative position of the transition state. For an early transition state, translational energy of the reactants will lead to an exothermic reaction and vibrationally excited products. For a late transition state, vibrational energy of the reactants will lead to an endothermic reaction and translationally excited products (high kinetic energy).

Nf710 (talk) 10:43, 26 May 2017 (BST) You could have proved the Polyanis rules with some examples using the HF system and you didn't completely answer some of the questions. Your understanding of TS theory was good.