MRD:ZZY115
Molecular Reaction Dynamics: Applications to Triatomic systems
Introduction
For a chemical reaction to take place, the reactants need to have sufficient energy to overcome the activation barrier. However, even if the activation barrier has been overcomed, the reaction doesn't have to proceed to the products. The progress of a chemical reaction with different set-up initial conditions can be predicted by plotting its trajectory on its potential energy surface. Those conditions involves atoms of reactants, the relative distance between them and their initial momentum. The motion of atoms is assumed to obey classical mechanics.
The collisions between an atom and a diatom molecule are studied here through calculating its molecular dynamics trajectories in MATLAB.

H + H2 system
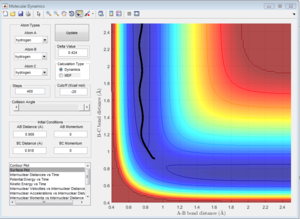
This is the simplest three atom system. A reactive trajectory of this system is shown below:
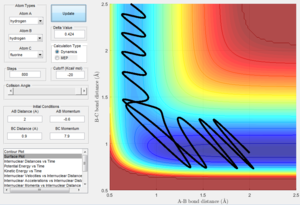
A negative momentum between two atoms means they are coming towards each other.
Dynamics from the transition state region
The activation energy is the energy difference between the transition state and the reactants. Transition state has the maximum energy on the minimum energy path from reactants to products. For the potential energy versus interatoms distance plot, i.e. the potential energy surface, the transition state is at a point with zero gradient, it is the local maxima. Trajectory starts from this point with zero momentum will remain at that point without going to either reactants or products.
The minimum energy structure is different from the transition state energy structure. The gradients of potential at this two points are both zero (∂V(ri)/∂ri=0). However, they have different secondary derivatives. A 2-dimension system is considered here. Secondary derivatives of both dimensions are greater than zero for the minimum energy structure as it has the lowest energy in both dimensions. For the transition state, one of the secondary derivatives is greater than zero while the other is smaller than zero. This is because transition state is the local maxima at one dimension in the minimum path of the other dimension (∂V2(r1)/∂r12 > 0 and ∂V2(r2)/∂r22 < 0 ).
Locating the transition state
The H + H2 system has a symmetric energy surface as the three atoms are identical. Therefore at transition state, r1 = r2. By setting p1 = p2 = 0, testing different r values to locate the transition state, where the atoms remain unmoved.
Here is the best estimate of the transition state position (rts).

The inter-nuclear distances don't change with time for a trajectory starts at the transition state.
Calculating the reaction path
The reaction path is the minimum energy path where the velocity always reset to zero in each time step, i.e. KE = 0. This can be calculated by slightly displacing from the transition state. This trajectory simply follows the valley floor of the potential energy surface. The initial conditions are set to be r1 = rts + 0.01, r2 = rts and p1 = p2 = 0.
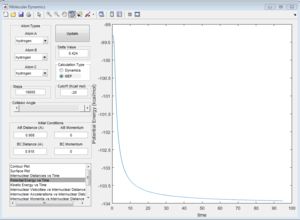
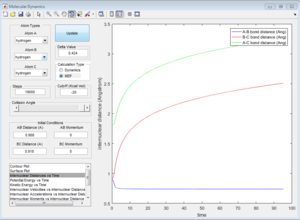


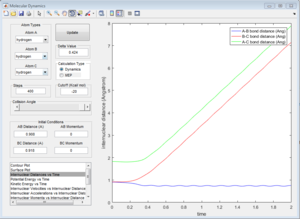
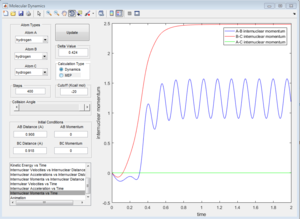
Mep doesn't predict a realistic motion of the atoms during reaction, it doesn't account the vibrationol motion of atoms showed in the dynamic calculations. Since Mep always reset the atom velocity to zero, the momentum of atoms remain zero while the momenta (p1 and p2) from dynamic calculation increase at first then remain constant at a non-zero value and the inter-nuclear distance (rAC and rBC) increase very slowly with time compared with the dynamic calculations.
Set the initial condition as r1 = rts, r2 = rts + 0.01 and p1 = p2 = 0. The reaction goes to the reactant direction. This trajectory is symmetrical to the previous one.
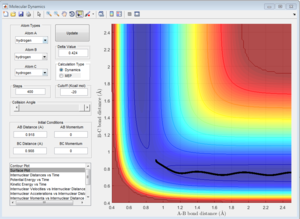
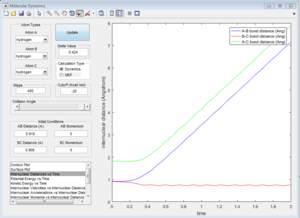
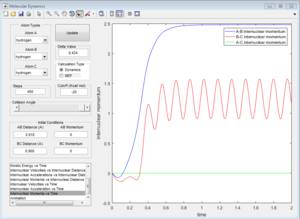
By setting the initial conditions corresponds to the final conditions of the trajectory but reversing sighs of the momenta. The products goes towards each other instead of moving further away, the reaction goes backwards from the products to the transition state region.

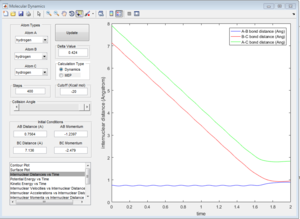
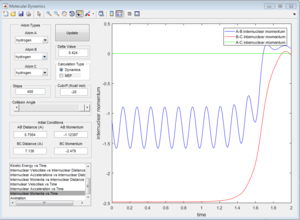
Reactive and unreactive trajectories
From the previous calculations it is known that trajectories with initial conditions in the range r1 = 0.74, r2 = 2.0, with -1.5 < p1 < -0.8 and p2 = -2.5 are reactive. However, trajectories with the same initial positions but with higher momenta are not reactive as we would assume. Those trajectories have enough kinetic energy to cross the activation barrier but the barrier can be recrossed and goes back to the reactants. The new bond forms transiently then break.
| p1 | p2 | Result |
|---|---|---|
| -1.25 | -2.5 | Reactive |
| -1.5 | -2.0 | Nonreactive |
| -1.5 | -2.5 | Reactive |
| -2.5 | -5.0 | Nonreactive |
| -2.5 | -5.2 | Reactive |
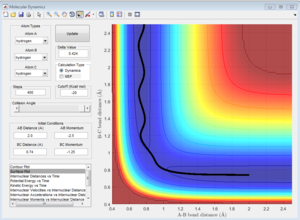

This trajectory is reactive, the reactants cross the activation barrier and go to the products.
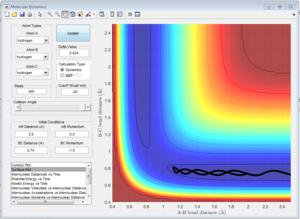
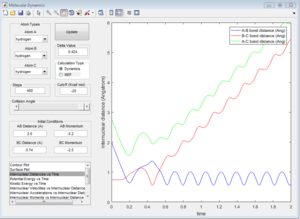
This trajectory is nonreactive, the reactants don't have enough kinetic energy to cross the activation barrier. The atom and molecule come towards each other at the start then direction of movement is reversed and they move away from each other.
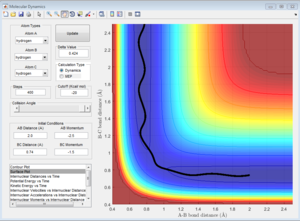
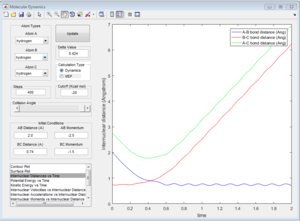
This trajectory is reactive, the reactants cross the activation barrier and go to the products.

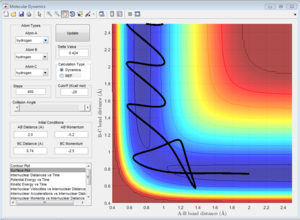
This trajectory is nonreactive, the reactants have enough kinetic energy to cross the activation barrier and bond forms transiently. However, the barrier is recrossed and the trajectory goes back to the reactants.
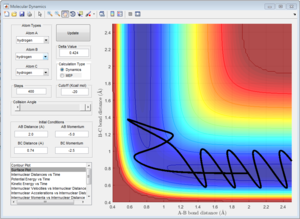
This trajectory is reactive, but the activation barrier is crossed twice.
The main assumption of the transition state theory is that the activation barrier is never recrossed, once the barrier is crossed the reaction goes to the products. However, in reality, the activation barrier can be recrossed and goes back to the reactants. This indicate that the reaction rate predicted by the transition state theory is much higher than the experimental value and don't allow time for the system to recross the activation barrier.
F - H - H system
There are two reactions possible for this system.
1.F + H2 reaction
2.H + HF reaction
PES inspection
F + H2 reaction
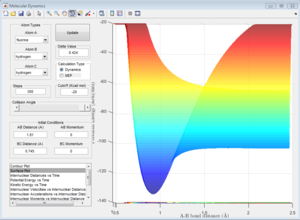
This reaction is exothermic since the potential energy of the reactants is greater than the products. This indicate that the strength of H-F bond is greater than that of the H-H bond.
The Hammond postulate states that transition state of a reaction resembles either the reactants or the products, to whichever it is closer in energy. For a exothermic reaction, the transition state structure resembles the reactants as they are close in energy. Therefore, the transition state location on the potential surface is close to the reactants.
The transition state of this reaction is located by setting the momenta as zero, however since this system is not symmetric due to different atoms present, r1 doesn't equal to r2 at the transition state.
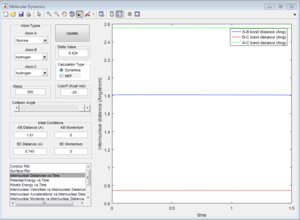
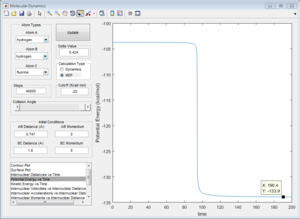
By performing a mep calculation from a structure neighbouring the transition state showing the reaction path, the activation energy can be found.

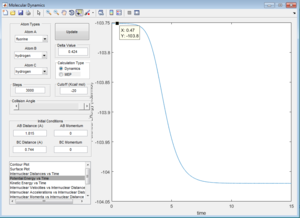
Activation energy = -103.8 - (-104) = 0.2 kcal/mol
H + HF reaction
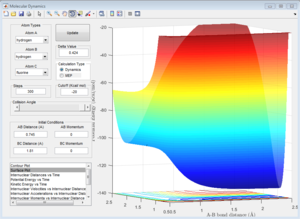
This reaction is endothermic since the potential energy of the products is greater than the reactants. This indicate that the strength of H-F bond is greater than that of the H-H bond.
According to the Hammond postulate, the transition state resembles the product and is close to the product region on the potential surface.
By performing a mep calculation from a structure neighbouring the transition state showing the reaction path, the activation energy can be found.
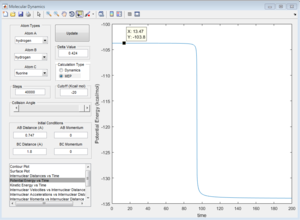
Activation energy = -103.8 - (-133.9) = 30.1 kcal/mol
Reaction dynamics
F + H2 reaction
Here is a reactive trajectory of this reaction. PHH = 0.1 PFH = -0.8 rHH = 0.74 rFH = 2
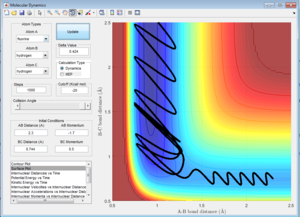
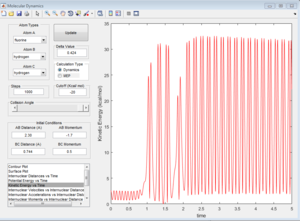
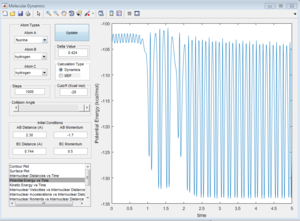
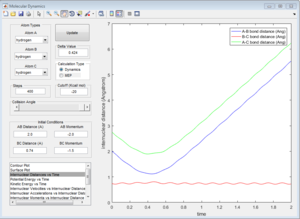
Since energy is conserved in the reaction, the sum of KE and PE remains constant throughout the reaction. For this exothermic reaction, the system has a high PE and a low KE. As the transition state is crossed, the potential energy of the system drops and transfer to kinetic energy, shown on the graph with an increase in KE and a decrease in PE. Also at the start of the reaction, there is a low vibrational motion on the system, the KE and PE don't fluctuate much. However the new H-F bond formed has a high vibrational motion, the molecules vibrates much intense, shown on the graph of large fluctuations of KE and PE (the KE and PE are inter-converted during vibration). In addition, the products move away from each other. In conclusion, the reaction energy released is converted to kinetic energy of the product in forms of vibrational energy and translational energy. The change in vibrational motion can be determined by IR spectroscopy.
The trajectories with the following initial conditions are calculated:
rFH=2 Å
rHH=0.74 Å
pFH=-0.5 kg m s-1
pHH in the range 3 kg m s-1 to -3 kg m s-1
| pHH | -3.0 | -2.5 | -2.0 | -1.5 | -1.0 | -0.5 | 0.0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Result | Unreactive | Unreactive | Reactive | Unreactive | Unreactive | Unreactive | Reactive | Unreactive | Unreactive | Unreactive | Unreactive | Reactive | Unreactive |
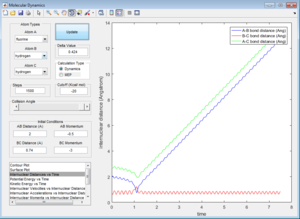
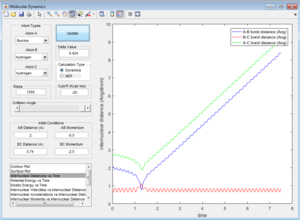
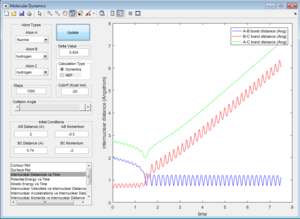

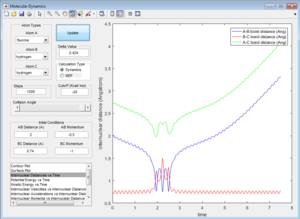
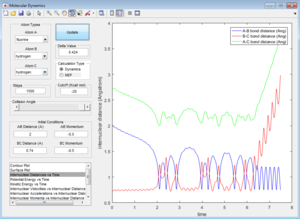
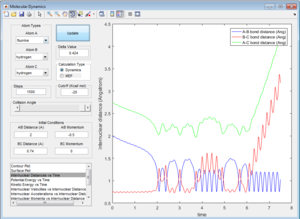


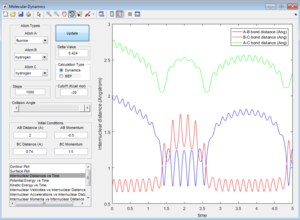


All the trajectories have more energy than the low activation energy of this reaction on the H-H vibration. However not all trajectories are reactive, some recross the activation barrier.
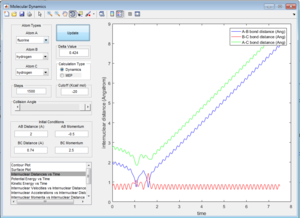
Increase slightly the pFH=-0.8, and reduce the overall energy by reducing the pHH=0.1. Keeping the distances the same.
This trajectory leads to products. It shows that system too high in energy is not always preferred and doesn't have to lead to a reaction.

H + HF reaction
Trajectory with a low vibrational motion on the H-F bond and an arbitrarily high value of pHH above the activation energy is shown below. rHH=2 rHF=0.91 pHH=-2.2 pHF=-2
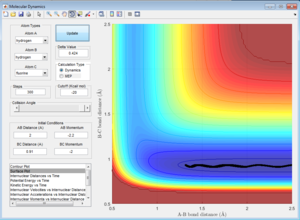
This trajectory is not reactive.
A reactive trajectory is obtained by decreasing the momentum of the incoming H atom and increasing the energy of the H - F vibration. pHH=-0.9 pHF=-8.5 r is the same as above.
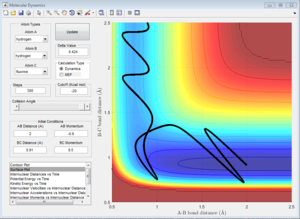
This trajectory has a high vibrational motion on the H-F bond.
The Polanyi's empirical rules states that the vibrational energy is more efficient in promoting a late-barrier reaction than translational energy. The H + HF reaction is endothermic and is a late-barrier reaction. The non-reactive trajectory above is an example of low vibrational energy and a high translational energy. The H atom moves fast towards the HF molecule with a low vibrational motion as the contributions of pHH and pHF on the H atom in the HF molecule cancels out. The reactive trajectory above is an example of low translational energy and a high vibrational energy. The pHH is very small and the pHF is very large, indicating high vibrational motion on the H-F bond, this is also shown on the potential surface plot. These two examples obey the Polanyi's emperical rules. The vibrational energy is more efficient in promoting a late-barrier reaction than translational energy. This rule doesn't apply to reactions with a early-barrier.
