MRD:ZN 01510257

Molecular Reaction Dynamics: Applications to Triatomic systems

This is a report written for the Molecular Reaction Dynamics Lab, due 22/05/2020. This is done by Zaeem Najeeb, CID : 01510257.

EXERCISE 1: H + H₂ system

Q1) On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?

The transition state is defined as the saddle point for a potential energy surface. This is a stationary point in a multivariate function (in our case where the variables are the AB and BC bond distances, with the z-axis defined as the potential energy of the system) where the gradient with respect to each orthogonal variable is zero. However, the curvatures (the second differential with respect to the same variable) are neither all positive or negative.

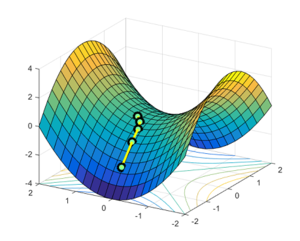
In general, the transition state can be found by analysing the hessian matrix. For our case, the hessian matrix is a 2 by 2 symmetric matrix comprised of the second differential with respect to each variable. If we then take the determinant of this matrix, denoted as D, we can then analyse the nature of the stationary point.

The determinant of a 2 by 2 hessian matrix. The variables are x and y in this case, where (x₀,y₀) denote the co-ordinates of the stationary point.[2]

When the value of D is calculated, a simple test for the nature stationary point is as follows:

If D>0 and f_xx>0, then (x₀,y₀) is a point of local minimum.
If D>0 and f_xx<0, then (x₀,y₀) is a point of local maximum.
If D<0, then (x₀,y₀) is a saddle point.
If D=0, then this test fails.

We can use this test to determine the transition state as the only case where the test could fail would be if D=0. This would not be possible in our physical system as this would require no curvature for the second partial derivatives to be 0. Given that the atoms are close together, there is no physical case where D=0 occurs so this test is sufficient for determining where the transition state is.

Good description. More clarity would be gained if you did analyse the matrix by showing how to calculate the sum of the matrix. Sf3014 (talk) 17:53, 3 June 2020 (BST)

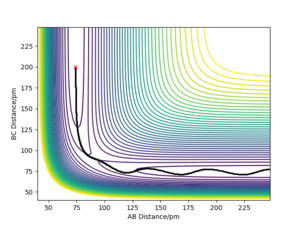
Q2) Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

The best estimate for the transition state position, r_ts, is r_ts≈ 90.775 pm.

This was determined by first considering a trajectory that resulted in a reaction. Due to the symmetric nature of the potential surface, as the energy level of the products and reactions is the same. This means that there is neither a late or early transition state, so by analysis using Hammond's postulate, the form of the transition state molecule gains equal contribution from the reactants and products. This leads to the AB and BC bond being equal when at the transition state, which is therefore also equal to the transition state position.

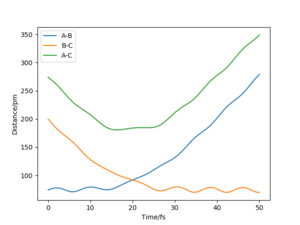
Using this plot, we are able to see that r_ts≈ 90 pm, however this can then be further improved by setting the AB and BC bond distances to 90 pm and the momenta of both as zero.

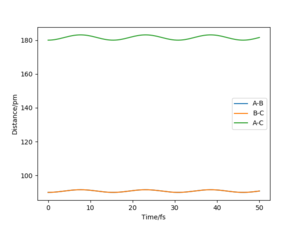
Given that the gradient at the transition state is zero, there should be no force at the stationary point. This is due to the force being equal to the negative of the gradient of a potential. By altering the value of r_ts, we can monitor how close we are to the transition state by seeing whether the calculated force is zero, which would also be when the triatomic molecule would no longer be moving. This occurs to 3 decimal places (the limit of the model used in this lab) at 90.775 pm, and can be seen by how the AB and BC bond distances no longer vary, suggesting that they are no longer oscillating.

Excellent description but even though the figures are in line with the text you should still refer to them within the text because the figures are easily ignored when reading through the text. Also, where did you get the information on Hammond's postulate? Reference needed Sf3014 (talk) 18:02, 3 June 2020 (BST)

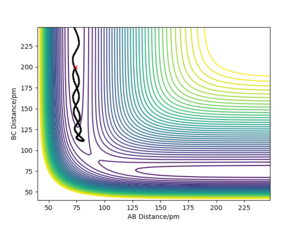
Q3) Comment on how the mep and the trajectory you just calculated differ.

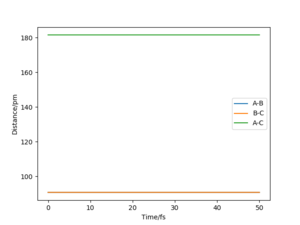
An mep calculation shows the trajectory of the system at infinitely slow time steps. This would mean that the momenta of the atoms is zero, so there should be no form of kinetic energy present. This can be seen by how the mep trajectory follows along the minimum potential energy value as the bond distance for BC does not vary (after forming H₂). This is done for the case of AB = r_ts+ 1 pm, BC = r_ts.

A dynamic calculation of this same system will the inertial motion of the atoms such that, when displaced in the same manner as the mep trajectory, oscillations of the BC bond length is observed. This is due to the potential energy being converted to kinetic energy in the form of vibrational motion.

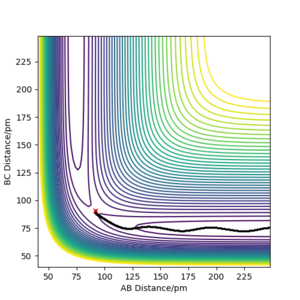
Comparing the 2, we would expect the dynamic trajectory to approach the mep trajectory as the temperature decreases. This would be due to the system approaching a state of no molecular vibrations when the temperature approaches 0 K. As the momenta are always zero in the mep trajectory, we can neglect kinetic energy and see how the potential energy changes. This would be useful for determining activation energies of the system by perturbing it from the transition state in a particular direction.

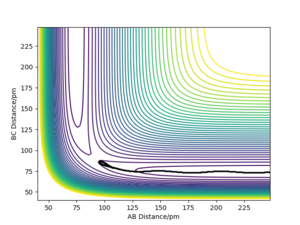
Another difference can be seen if we attempt to get the final positions of the trajectory and reverse both momenta. For the dynamic trajectory, this will effectively retrace the trajectory it took and return to the transition state. It will never overcome the transition state as, due to conservation of energy, the total energy of the system is lower than the transition state. This is due to the initial conditions placing the system slightly below the transition state with no momenta.

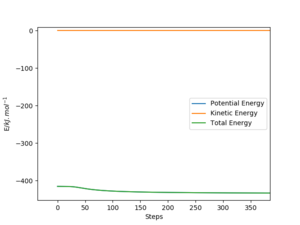
However, this fails for an mep calculation as there is no momenta at any point in time. The energy that would have been converted to kinetic energy is effectively lost in the process of moving from the transition state due to the momenta constantly being zeroed. This highlights how mep is unrealistic as this would break the conservation of energy.

If we were to now instead displace via is done for the case of AB = r_ts, BC = r_ts+ 1 pm then the same trajectories will occur, but instead the AB molecule will form. This would appear as a mirror image of the previous displacements about the y=x axis. This is due to the symmetric nature of this system.

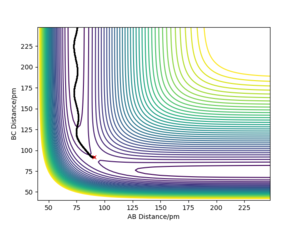
Very good discussion but again refer to graphs, especially when you talk about the lack of momenta in mep calculation, state that it can been seen in figure X, from the zero kinetic energy Sf3014 (talk) 18:09, 3 June 2020 (BST)

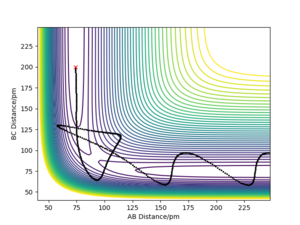
Q4) Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?

Below is a table recording the observations of a H₂ + H reaction, where each H is denoted as either A, B or C respectively. This therefore is equivalent to a AB + C reaction. The initial position of each reaction was AB distance = 74 pm and BC distance = 200 pm. The time step used in the trajectories is at 0.1 fs.

p₁/ g.mol^-1.pm.fs^-1	p₂/ g.mol^-1.pm.fs^-1	E_tot	Reactive?	Description of the dynamics
-2.56	-5.1	-414.28	Yes	Here the non-vibrating AB molecule collides with C, forming a vibrating BC molecule and A which moves away at a greater velocity than when in the AB molecule.
-3.1	-4.1	-420.08	No	The vibrating AB approaches C, however the collision occurs such that the transition state does not form. The vibrating AB and C move apart.
-3.1	-5.1	-413.97	Yes	This is a similar case to the 1st situation, except now AB has enough momenta to have significant vibration energy, and so is vibrating. The form BC is also vibrating, with A moving away.
-5.1	-10.1	-357.10	No	AB approaches C, leading to to a successful collision which produces a strongly vibrating BC. This BC manages to then interact with A, leading to a second collision where AB is reformed and now strongly vibrating and C moves away fast enough to prevent further recrossing.
-5.1	-10.6	-349.48	Yes	This is a similar case to the 4th system. However, C does not move away fast enough so a second recrossing occurs due to the interaction between the strongly vibrating AB molecule and C. This leads to products forming.

From this table we can see that even though the kinetic energy of the system was sufficient to successfully react, as seen in the 1st trajectory, the different momenta effect whether phenomena such as recrossing, or even reaching the transition state is possible. This could be due to the different bond momenta leading to different phases of vibration upon collision. This would explain why the 1st and 3rd case differ in success, as if there is significant vibration, the point of reaction is no longer the same. This would also suggest an explanation for the final 2 cases of recrossing, where the slight difference in momenta altered the vibrations enough that one trajectory was able to recross again whilst the other was stuck back at the reactants.

Good table layout but your conclusion is a little hard to follow. When talking about vibrations it's best to label p1 and p2 with respect to the AB and BC distances. Also, label the "cases" in your table Sf3014 (talk) 18:19, 3 June 2020 (BST)

Q5) Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

The three main assumptions in transition state theory are:

Systems that have surmounted the transition state barrier cannot go back to reform the reactants
The energy distribution among the reactants is in accordance with the Maxwell-Boltzmann distribution
A chemical reaction can be treated in terms of classical motion. Quantum effects can be ignored.[3]

When comparing this to our system, we see that the first assumption is clearly false in the form of recrossing at specific momenta. This leads to transition state theory overestimating the reaction rate as more products are assumed to be formed when the bulk system is considered.

However, we can also see that the 3rd assumption is also false as in reality energy the vibrational modes are quantised is energy. Similarly effects such as quantum tunnelling are ignored which would allow reactants of lower energy to form the products. This would increase the reaction rate.

Therefore, transitions state theory fails to account for phenomena such as quantum tunnelling and recrossing, leading to this model failing to represent the experimental values.

Very good and clear description. Where did you get the information on transition state theory? Sf3014 (talk) 18:22, 3 June 2020 (BST)

EXERCISE 2: F - H - H system

For the following systems, A=F atom and B,C = H atom.

Q6) By inspecting the potential energy surfaces, classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

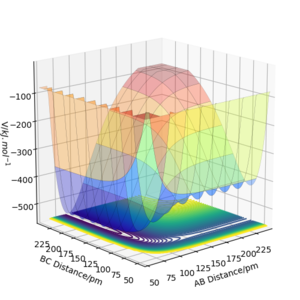
Looking at the potential energy surface we can see that the AB bond is more stable than the BC bond. This is shown with how the potential energy of the AB bond is much lower than that of the BC bond when in a stable state. This matches literature values where the H-F bond dissociation energy is 565 kJ.mol^-1and the H-H bond dissociation energy is 432 kJ.mol^-1 and is due to large difference in electronegativities between H and F producing significant ionic effects that contribute to the bonding[4]. This also shows how the reaction of FH + H → F + H₂ must be endothermic, with the reverse being exothermic. We can see this on the potential energy surface as the process of going from BC to AB includes a large drop in potential energy, showing that the formation of HF is favoured.

Good. Your link to the website for the bond energies shows a references at the bottom of the page for the information on it which your could of used as your own reference Sf3014 (talk) 18:27, 3 June 2020 (BST)

Q7) Locate the approximate position of the transition state.

The approximate position for the transition state was located at AB = 181.04 pm and BC = 74.49 pm, where A= F atom and B, C are H atoms.

To locate the approximate position for the transition state for an asymmetric system, we can no longer assume that AB distance = BC distance when at the transition state. Instead, by knowing that the formation of HF is highly exothermic, the transition state can be assumed to resemble the reactants. This is according to Hammond's postulate where an exothermic reaction will have an early transition state. The first assumption therefore would be a BC distance of 74 pm and an AB distance of 100 pm as the transition state should closely resemble a H₂ + F system (The momenta are kept as zero).

Looking at the result of the first approximation, we can visually see that the AB distance is too small. This can also be seen by the relatively large force along the AB bond. The AB bond distance was therefore increased until the force along the AB bond was considered zero to 2 decimal places by the interface to produce the second approximation where AB = 178.5 pm and BC = 74 pm.

At this point, there is still forces present along the AB and BC bonds, however these forces are no longer independent of each other. Therefore, to produce the final approximation for the transition state both bonds were altered until the force along them were zero to 3 decimal places. This occurred when AB = 181.04 pm and BC = 74.49 pm.

We can then confirm this is the case by looking at the internuclear distance against time plot to see no oscillations occur, as done with the H₂ + H system.

Very good description on how you find the transition state distances Sf3014 (talk) 18:31, 3 June 2020 (BST)

Q8) Report the activation energy for both reactions.

Given that the coordinates for the transition state are known, we can perturb the system slightly to induce the the reactants to fail to overcome this transition energy and return to the reactants. This was done for both the exothermic and endothermic reaction pathways. The activation energy can therefore be calculated by taking the difference between the transition state energy, E_TS ,with the energy at equilibrium, E_End. This can be seen by looking at the change in energy of the system in an mep calculated trajectory. A large number of steps were considered to ensure that the potential energy had reached a fixed value.

The reaction pathway is referring to the direction the reaction would have occurred if the reaction was successful. As they are unsuccessful, this will show the energy difference between the reactants and transition state energy. This highlights the relatively small barrier of HF formation from H₂.

Reaction pathway	E_TS/kJmol^-1	E_End/kJmol^-1	Activation energy/kJmol^-1	Energy vs time plot	Energy vs time plot zoomed in	Initial conditions used	Percentage error
FH + H → F + H₂	-433.981	-560.290	126.309			AB = 180.04 pm BC = 74.49 pm Both momenta are 0 Time step of 0.1 fs	5.84 %
H₂ + F → HF + H	-433.981	-435.013	1.032			AB = 182.04 pm BC = 74.49 pm Both momenta are 0 Time step of 0.1 fs	71.32 %

The activation energies were compared with experimental values to find a relatively small error for H₂ formation compared to the error for HF formation [5]. This is likely due to the systems resolution being too large to accurately approximate the much smaller activation energy. When the activation energy is large however, the model worked within an acceptable range.

Very good. Your reference is not linked properly to give a reference list, details on this was in the reference section of the "wiki page instructions". How was your error calculated? Also, there is no need to speculate why the values are different because the theoretical study will explain why they may be different based on the use of different models to calculate the values Sf3014 (talk) 18:43, 3 June 2020 (BST)

Q9)In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.

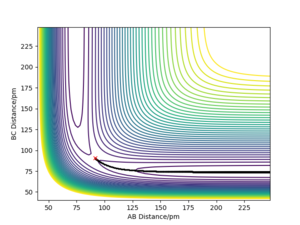
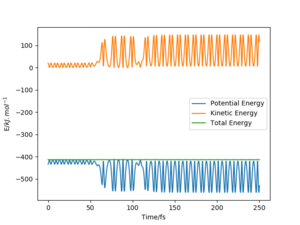
A set of initial conditions for a reactive trajectory of the F + H₂ reaction, where A= F atom and B, C are the H atoms was used to demonstrate the release of reaction energy. This was done with AB distance = 200 pm, BC distance = 74 pm, AB momentum = -1 g.mol^-1.pm.fs^-1and the BC momentum = -5 g.mol^-1.pm.fs^-1. A time step of 0.1 fs was used and the reaction was observed for 2500 steps.

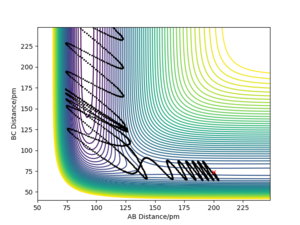
This initial conditions show a successful reaction after multiple recrossings occur. As conservation of energy applies to this model, and the reaction is exothermic, the loss in potential energy due to a successful reaction must still be present in the system. This potential energy is converted to kinetic energy in the form of vibrations.

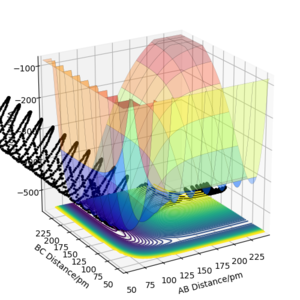
We can further confirm this by looking at an energy against time plot, where we can see how the kinetic energy has a much greater variation than before the reaction at roughly 60 fs. This also shows how the kinetic energy has increased on average, and therefore the lost potential energy due to the exothermic reaction must have been converted into some form of kinetic energy.

We can experimentally confirm that the system has released potential energy as vibrational kinetic energy via absorption IR. This is because higher vibarational modes would become excited upon successful reaction. Therefore, unlike the relaxed system which is primarily composed of molecules in the ground state vibrational modes, the 1st excited state would now also be significantly populated. This would allow for absorption of IR wavelengths from the 0 to 1st level (the 0 to 1 fundamental peak) and the now significantly populated 1st to 2nd level (a 1 to 2 hot band). Experimentally, this would appear as a smaller peak to the left of the main vibrational peak. If measured over a given time period, the smaller peak would be expected to decrease in size whilst the main peak would increase. This is due to the higher vibrational states relaxing over time and losing energy via several means [6].

Very good. What kind of set up would allow for data collection as the reaction proceeds, for your stated experiment? Sf3014 (talk) 18:48, 3 June 2020 (BST)

Q10)Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state

The table below contains the initial conditions used for a calculated dynamic trajectory of the F + H₂ reaction where A = F atom and B, C are the H atoms. The AB distance = 200 pm and the AB momentum = -1 g.mol^-1.pm.fs^-1. The BC distance = 200 pm. The time step is 0.1 fs and each trajectory is calculated for 4000 steps. The BC momenta is changed as shown in the table, with the animation and contour plot shown.

p₂/ g.mol^-1.pm.fs^-1	Reaction successful?	Animation of trajectory	Illustration of the trajectory
5	No
3	Yes
1	Yes
0	Yes
-1	Yes
-3	No
-5	Yes

Polanyi's empirical rules state that an exothermic reaction (early transition state) will favour translational energy over kinetic energy for a successful reaction. This is the opposite when an endothermic reaction (late transition state) is considered [7]. When considering the exothermic reaction of HF formation, this would mean that systems with smaller kinetic energy are more likely to react successfully, assuming sufficient translational energy is supplied.

This can be explained by how the reactants in an endothermic reaction must go up a steep barrier to react the products on a potential energy surface. If there is no kinetic energy present, then the reactant does not vibrate and therefore the reactants will 'bounce off' the potential energy surface as they have no way to move in the orthogonal direction to reach the product path. Similarly, if the reactants for an exothermic reaction had kinetic energy, they would oscilate in the potential energy surface, hindering the ability to 'fall down' to the products.

A trend seems to appear when considering momenta of BC between 3 and -1 g.mol^-1.pm.fs^-1, however a discrepancy is seen when the absolute value of BC is 3 or 5 g.mol^-1.pm.fs^-1. In both cases, although the kinetic energy is the same (as it is proportional to the momentum squared), the success of the reaction differs. This could be due to the phase of the vibrational mode causing recrossing to occur 1 too many times, leading to an unsuccessful reaction.

This suggests that Polanyi's rule works when there is a significant difference in the translation and kinetic energies, as seen by the reactions all being successful when |BC|<3 g.mol^-1.pm.fs^-1. However, other factors such as the phases of the momenta and potentially even collision angle become significant factors in the determination of the reaction efficiency.

Very good. Small mistake in the initial conditions above the table, the AB and BC distances are both written as 200 pm, but graph clarifies this. What about the endothermic reaction? Sf3014 (talk) 18:53, 3 June 2020 (BST)