MRD:YQ816
Molecular Reaction Dynamics: Applications to Triatomic systems
H + H2 system

In this model, hydrogen atom H3 collides with hydrogen molecule H1-H2 to give H1 + H2-H3. For a more convenient illustration, A, B and C refers to H1, H2 and H3 correspondingly.
A set of values including the distance(r) and momentum between AB(p) and between BC was set to obtain a system based on the energy changes.

Dynamics from the transition state region
Before the collision, the first derivative of the potential energy against rAB is zero because they need minimum potential energy to stay bonded; It is not really they 'need' minimum potential energy to stay bonded. It is because the system is the most stable at the minimum energy level. In other word, they don't need minimum energy to stay boned. Any energy as long as it doesn't go over the threshold, the molecule can stay bonded.--Sw2711 (talk) 14:55, 31 May 2018 (BST)the first derivative of energy rBC is greater than one Greater than one?--Sw2711 (talk) 14:55, 31 May 2018 (BST)because the potential energy increases during approaching. After the collision, the property is the same but in opposite way. At the transition state, both the first derivatives becomes zero because both the interactions between AB and BC changes in order to form or break a bond. This is your biggest mistake in this question. The two component to look for the minimum and maximum is not from AB/BC coordinate. It is a minimum at the diagonal of AB/BC plane and a maximum at the reaction coordinate plane--Sw2711 (talk) 14:55, 31 May 2018 (BST)However, the second derivatives are not zero. Instead, the second derivative is positive for potential energy between AB and negative between BC during the transition state. So here, it is not very true either. --Sw2711 (talk) 14:55, 31 May 2018 (BST) This can also be proved by the diagram. These properties can help distinguish the minimum energy and the transition states by measuring the first derivatives against both distance between A and B and distance between B and C.
I feel like you sort of getting the concept, but the way you described it is quite weird. I have left comments in your answers. Hopefully you can improve next time. --Sw2711 (talk) 14:55, 31 May 2018 (BST)
Trajectories from r1 = r2: locating the transition state
This part is good.--Sw2711 (talk) 14:55, 31 May 2018 (BST)
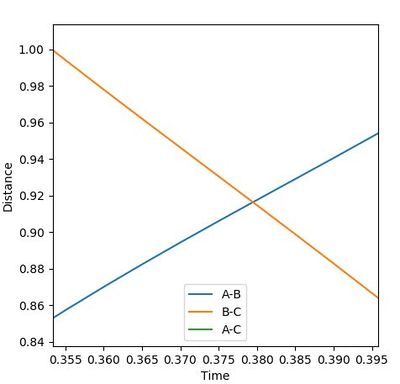
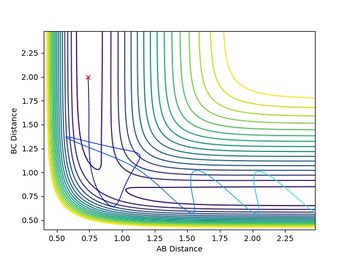
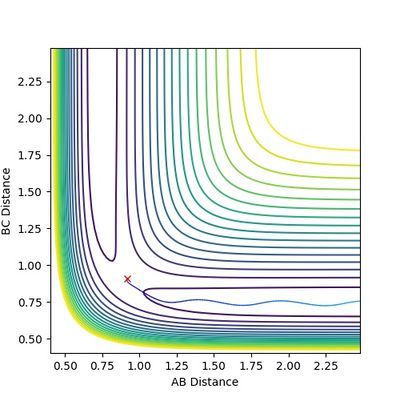
The diagrams (Figure 3.1 and 3.2) when rAB(0) = 0.74 rBC(0) = 2.30 and pAB(0)=0 pBC(0) = -2.7 was inspected. The interception of A-B and B-C line indicates that A and C are as far away from B,so the transition state position is near this point which is approximately (3.8, 9.2).
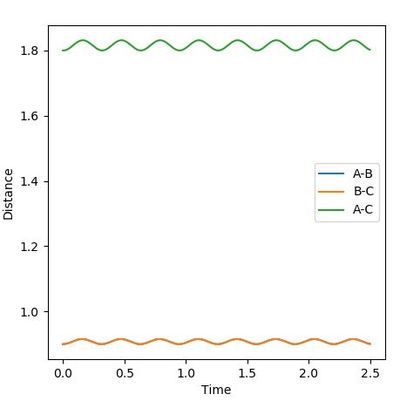
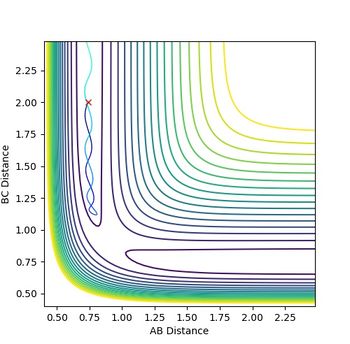
Therefore, rAB=rBC=0.90 was first tried as shown in Figure 4. The wave-like diagram indicates the vibration of A and C around the transition state position. The starting part shows that the molecules first went apart, meaning that the attempt is smaller than the real rts
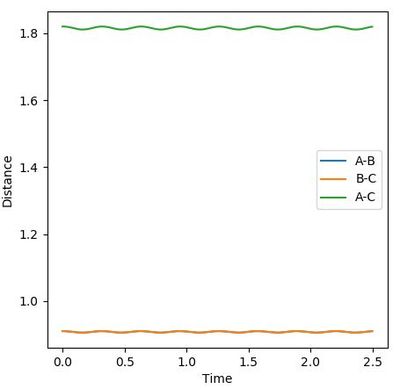
rAB=rBC=0.91 is then tried (Figure 5). There is still vibrations shown although with lower amplitude. However, This number is slightly larger since the lines start with decrease. Therefore, the real value should lie between 0.90 and 0.91. A number between 0.905 and 0.910 is tried.
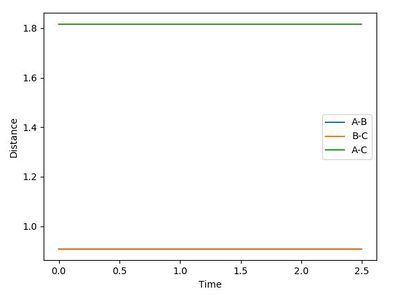
More attempts with higher accuracy was tried and the generated diagrams were judged, until the lines become flat as shown in Figure 6, which means the atoms fix in the location where it is initially. The value under this situation (0.90775 ±0.00005 a.u.) is then the transition state position. (As the diagrams when rAB = rBC is equal to 0.9077 and 0.9078 both show slight vibrations, but any values between gives almost as flat lines, the uncertainty of ±0.00005 a.u. is deduced here.)
Trajectories from r1 = rts+δ, r2 = rts
rBC was set to be rts (0.90775 a.u.), and rAB was set to be rts+0.01 (0.91775 a.u.), while the initial momenta among the atoms are all 0. The results were calculated using both minimum energy pathway (mep) and dynamic (500 steps).

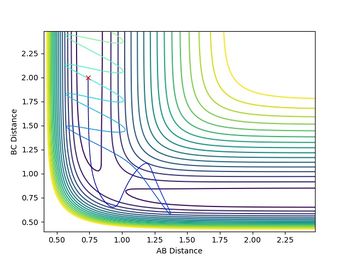
Both diagrams (Figure 7.1 and Figure 7.2) tell us that the reaction had passed the transition state, and the H2-H3 (the product) bond was formed.
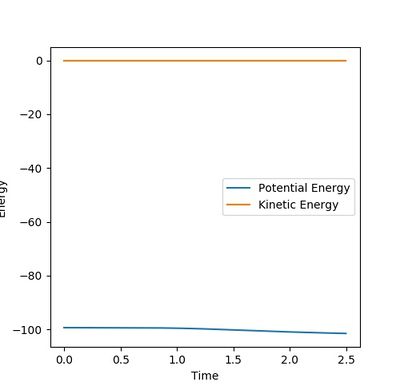
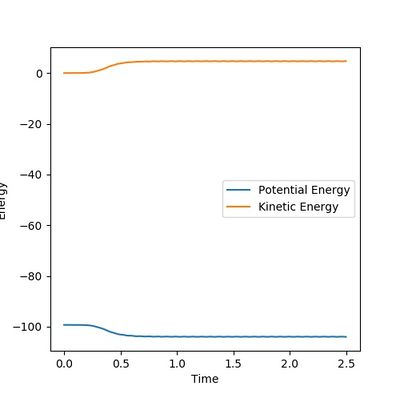
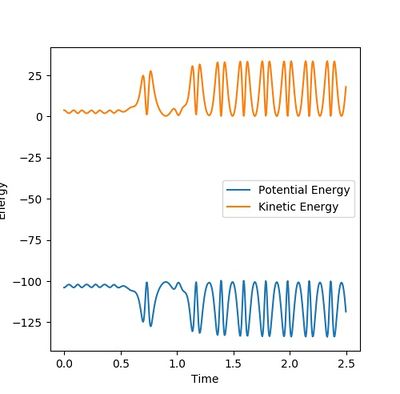
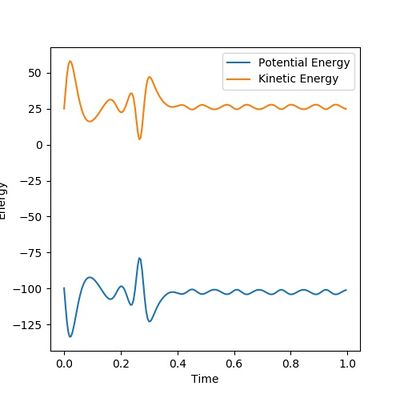
In the dynamic calculation The potential energy was transferred to kinetic energy which was 0 initially. (Figure 7.3) The kinetic energy was contributed by the vibrational energy of the H2-H3 molecule and the translational energy. The total energy is always reserved. This result is closer to the reality.
In the mep calculation, however, the potential energy decreased as shown in Figure 7.4, but this calculation doesn't have to take account of the kinetic energy as time elapse and the initial momenta are all 0 so that the kinetic energy remains 0. This makes the total energy not concstant. constant--Sw2711 (talk) 14:59, 31 May 2018 (BST)This calculation cannot give the real reaction dynamic but a clearer presentation of how the potential energy can reach and progress for every coordinators so that the activation energy can be found.
I think you mixed up Figure 7.3 and 7.4 with your explanation. Otherwise, it is good. --Sw2711 (talk) 14:59, 31 May 2018 (BST)
Reactive and unreactive trajectories
This part is good--Sw2711 (talk) 15:01, 31 May 2018 (BST)
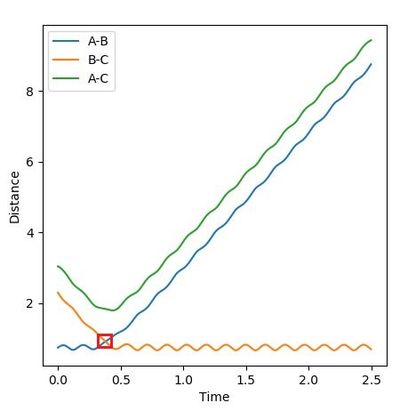
For the same initial positions rAB = 0.74 and rBC = 2.0, different results from different initial momenta were obtained:
Assumptions of Transition State Theory
In the transition state theory (TST), the analysis on the kinetics of the hydrogen particles is mostly based on classical mechanics. It does not take account of the quantum-tunneling effect, and the relative effect of the electrons on the nucleus is neglected (in other words, Born-Oppenheimer approximation is applied).[1] This greatly simplifies the calculation while the errors that may occur are negligible.
TST also assumes the equilibrium to be maintained during the reaction, which means that the ideal Boltzmann distribution keeps applied along the reaction coordinator. [2]. If the equilibrium is disturbed towards the reactants, the TST would predict a higher activation energy, and vice versa.
The other postulate is that the reactants can not re-cross the transition state and go back to the products.[3] However, inreality, as we can see in the calculation above, the results can be greatly biased if the system is under some extreme conditions such as high temperature when the reactants can re-cross the transition state several times, so that it is more complex to predict the precise reaction rate.
This part is also good. Just one minor point, 'equilibrium' and 'distribution' are not very applicable here. Because they are mainly used to describe in statistical thermodynamics. We only have 3 atoms in the system. So there isn't really an 'equilibrium' for us. --Sw2711 (talk) 15:04, 31 May 2018 (BST)
F - H - H system
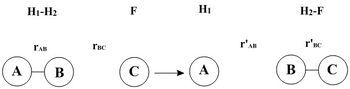
In this model, fluorine atom F collides with hydrogen molecule H1-H2 to give H1 + H2-F. For a more convenient illustration, A, B and C refers to H1, H2 and F correspondingly.

In the other model, hydrogen atom H2 collides with hydrogen fluoride F-H1 to give F + H1-H2. For a more convenient illustration, A, B and C refers to F, H1 and H2 correspondingly.
PES inspection
Reaction type and the bond strength
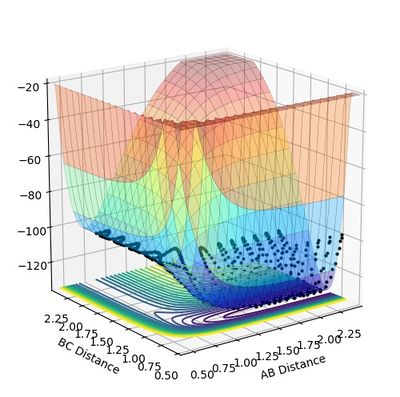
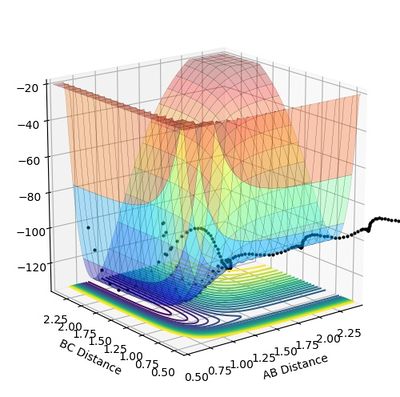
From Figure 10.1 and 10.3, it can be seen that the minimum potential of the reaction decreases along the reaction coordinators. During the reaction the potential energy transfers to the kinetic energy reflected as heat macroscopically. This is hence a exothermic reaction.
Figure 10.2 and 10.4 shows that the minimum potential energy increases during the reaction. Energy (i.e. heat) is required to enable the successful reaction. Thus, the reaction type is endothermic.
According to the literature value, the bond strength of H-H is 436 kJ/mol and that of H-F is 568 kJ/mol.[4] Fot the reaction H2 + F → H + HF, the H-H bond needs 436 kJ/mol of energy to be broken while the formation of the H-F bond releases 569 kJ/mol of energy. This manifests that this is a exothothermic reaction. For the reverse reaction, the process and the result are opposite.
Good, but do you think you can determine whether it is exo/endo reaction directly from the PES in Figure 10.1? Do you think you can figure out which bond is stronger by reading the PES only?--Sw2711 (talk) 15:07, 31 May 2018 (BST)
The transition state

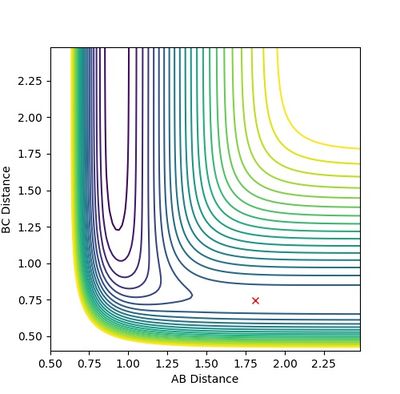
With Hammond's postulate, it is found that, when rAB = 0.7444 a.u. and rBC = 1.8110, the H2+F system is at the transition state (Figure 11.1 and 11.2). For the reverse reaction, the coordinator is reversed as well.
Good, but I think I need a better plot to convince me it is a TS point than the PES plot--Sw2711 (talk) 15:08, 31 May 2018 (BST)
The activation energy
This part is good.--Sw2711 (talk) 15:09, 31 May 2018 (BST)
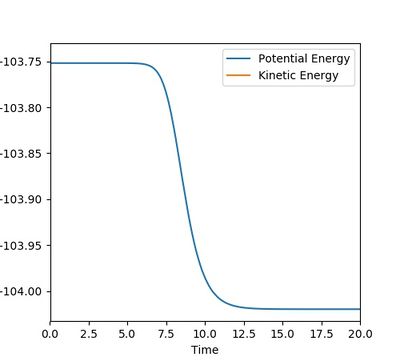
Figure 11.1 shows that, in the H2+F system, the energy decreased from -103.751 kJ/mol (potential energy at transition state) to -104.02 kJ/mol (potential energy at transition state), starting as the BC distance was 0.001 a.u. larger than that of the transition state. The total energy change is ~ -0.3 kJ/mol and hence the activation energy was 0.3 kJ/mol. This is a relatively small value, meaning that this reaction needs very little external energy to become spontaneous.
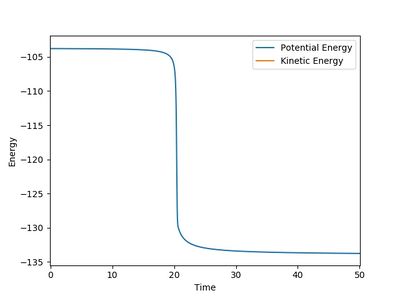
The energy change in the HF+H system, as given in Figure 11.2, was (-133.749) - (-103.755)= -30.0 kJ/mol when the AB distance was set 0.1 a.u. smaller than that at the transition state. Thus, the activation energy is 30.0 kJ/mol, shich means it indeed needs more energy than H2+F system to be reactive.
Reaction dynamics
Mechanisms
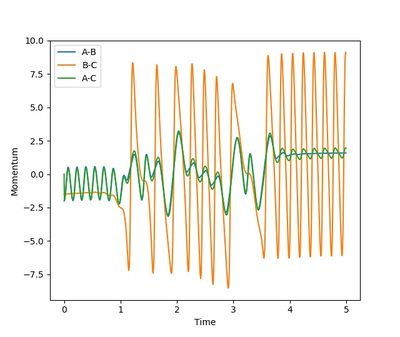


From the momentum plot, it can be observed the product HF vibrates more intensively than the reactant H2. This means a increase in vibrational energy. Also, the momentum between leaving atom and the molecule after the reaction is greater than the approaching atom and the molecule before collision. This shows a increase in translational energy. Overall, the momentum increased along the reaction coordinator. Some of the potential energy transferred to kinetic energy, resulting in these increase.
Experimentally, IR spectra can be used to visualize this change. The vibration frequency remained constant, but the intensity increased. As a result, there can be seen a peak at the same position on both IR spectra for the reactant and the product, but the peak for the product should be higher than that for the reactant. I am not sure I understand your IR experiments here. Do you mean the peak position (i.e. the wavenumber) for the product (HF) and the reactant (HH) is the same. But there will be a difference in the intensity of the peak? --Sw2711 (talk) 15:15, 31 May 2018 (BST)Temperature is a more intuitive property that can also manifest the increase in the kinetic energy since the temperature rises.
Polanyi's empirical rules
H2 + F → H + HF is a exothermic reaction. By Hammond's postulate, it has a early transition state. The translational energy that push the reagent together gives more contribution to the reaction efficiency than the vibrational energy which though can lead the system across the transition state, it is very likely to go back if the vibrational energy is too high.
H + HF → H2 + F system, on the other hand, is a endothermic reaction with a late transitions state. Vibrational energy is more important for the reactivity energy in light of overcome the H-F bond. Translational energy does not give much merit in the formation of H-H bond. [5]
Good literature research. I'd like to some of your opinion. Do you agree or disagree with the Polanyi's Rules?--Sw2711 (talk) 15:18, 31 May 2018 (BST)
References
- ↑ T. Bligaard, J.K. Nørskov (2008). in Chemical Bonding at Surfaces and Interfaces
- ↑ Luis Arnaut, Sebastiao Formosinho, Hugh Burrows (2007). 6 – Reactivity in Thermalized Systems "in Chemical Kinetics: From Molecular Structure to Chemical Reactivity"
- ↑ "Activation Energy and Temperature Dependence, Boundless Chemistry"
- ↑ Chung Chieh "Bond Lengths and Energies"
- ↑ Schreiber, J. C. (1977). The reaction of F + H2→ HF + H. A case study in reaction dynamics. Faraday Discussions of the Chemical Society, 267-290.