MRD:WXY0119

Molecular Reaction Dynamics Report

EXERCISE 1ː H + H₂ SYSTEM

In the H + H₂ system, the distance between the first two H atoms (m₁, m₂) is r₁ and the distance between the two H atoms in the H₂ molecule (m₂, m₃) is r₂.

Dynamics from the transition state region

Question 1 ː What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

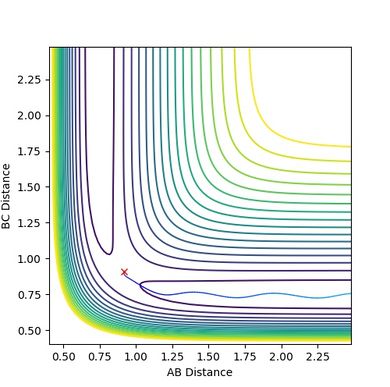
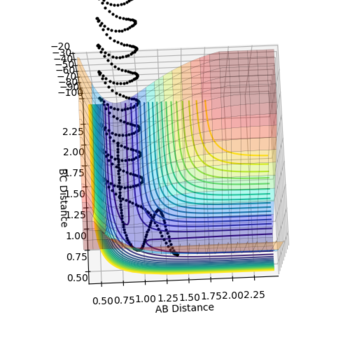
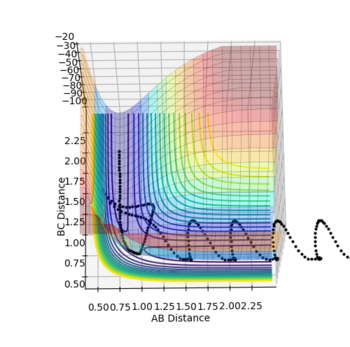
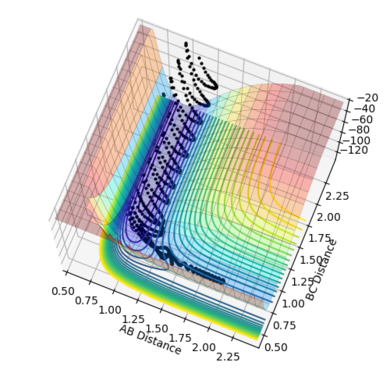
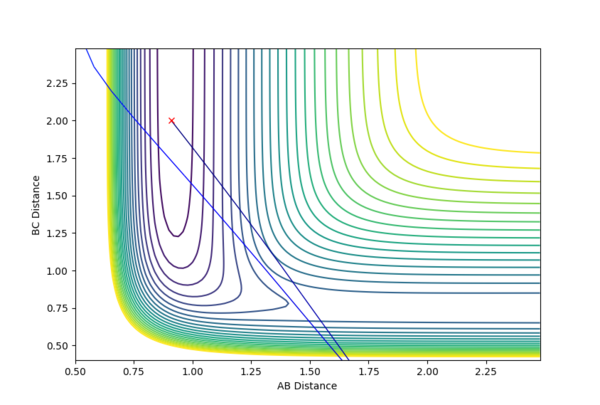
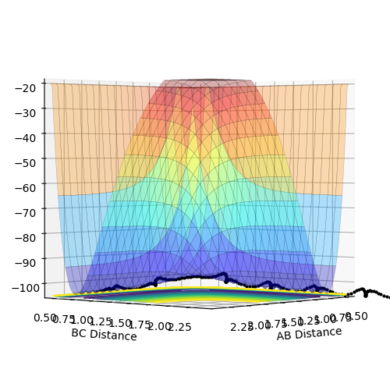
Figure.1 Surface plot of reaction trajectory	Figure.2 Transition state surface plot	Figure.3 Transition state surface plot (different angle)

In the reaction trajectory surface plot (Fig.1), AB is the distance r₁ and BC is the distance r₂. The gradient of the potential energy with regard to r₁ and r₂ are ∂V(r₁)/∂r₁ and ∂V(r₂)/∂r₂ respectively. The second derivatives of the potential energy with regard to r₁ and r₂ are ∂²V(r₁)/∂r₁² and ∂²V(r₂)/∂r₂² respectively.

At the two minimum structures which are at the two ends of the reaction pathway, ∂V(r₁)/∂r₁ = 0 and ∂V(r₂)/∂r₂ = 0 respectively. Since the two minimum structures are at two local minimum point , the second derivatives ∂²V(r₁)/∂r₁² and ∂²V(r₂)/∂r₂² are both greater than zero.

On the other hand, the components at the transition state structure (Fig.2) are different from that at minimum points. The gradient ∂V(r₁)/∂r₁ and ∂V(r₂)/∂r₂ are both equal to zero at the transition structure. However, ∂²V(r₁)/∂r₁² >0 and ∂²V(r₂)/∂r₂² <0. The transition state point is actually a saddle point which is observed more clearly in Fig.3. The Transition state point is thus distinguished from the minimum points as the potential energy surface curves inwards and downwards at the minimum points.

Mm10114 (talk) 15:45, 29 May 2018 (BST) Nice and clear.

Locating the Transition State

Question 2ː Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

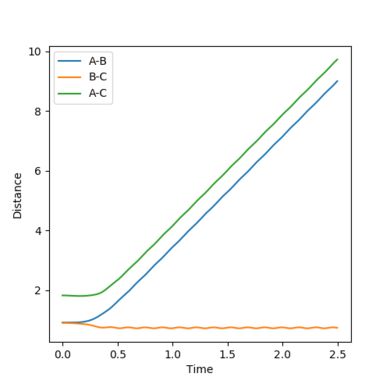
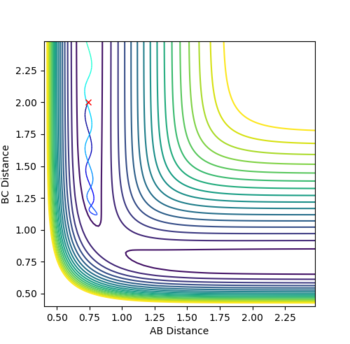
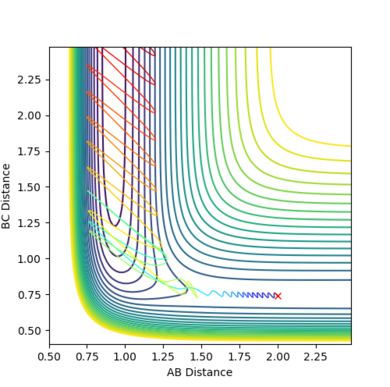
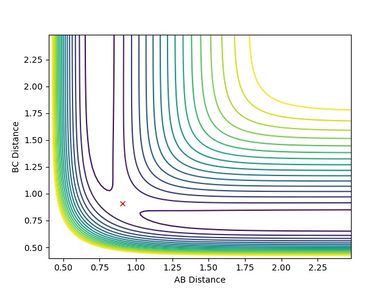
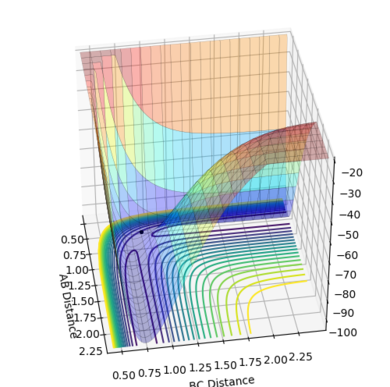
Figure.4 Transition state contour plot	Figure.5 Transition state surface plot	Figure.6 Internuclear distance against time plot

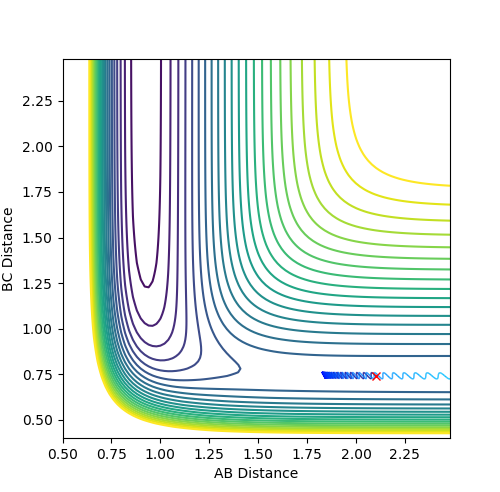
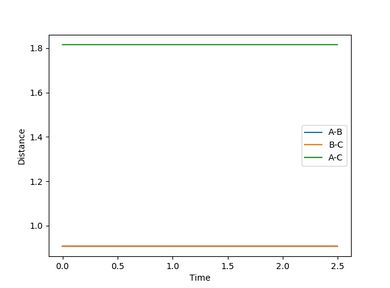
The best estimate of the transition state position is r_ts = 0.9078 Å.

When r₁ = r₂ = r_ts and momenta are set to zero, a graph of intermolecular distance against time is plotted. (Fig.6) In this graph, AB and BC lines are the same and overlap, the two lines on the graph are flat and horizontal, indicating that the atomic distances are the same at the position and with no momenta the state is at equilibrium, validating the position is the transition state position. The transition state is shown as a cross on the counter plot (Fig.4) and a dot on the surface plot (Fig.5).

Mm10114 (talk) 15:48, 29 May 2018 (BST) Nicely done. Just worth thinking through: Would you expect the “Internuclear Distances vs Time” plot to stay the same if you would considerably increase the length of the simulation (number of steps)? Why/Why not?

Calculating and comparing the reaction path and trajectory

Question 3ː Comment on how the mep and the trajectory you just calculated differ.

Figure.7 mep calculation contour plot	Figure.8 mep calculation surface plot	Figure.9 mep calculation internuclear distance against time plot
Figure.10 Dynamics calculation contour plot	Figure.11 Dynamics calculation surface plot	Figure.12 Dynamics calculation internuclear distance against time plot

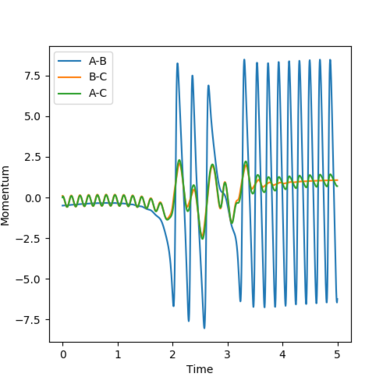
Figure.13 Dynamics calculation internuclear momenta against time plot	Figure.14 mep calculation internuclear momenta against time plotsurface plot

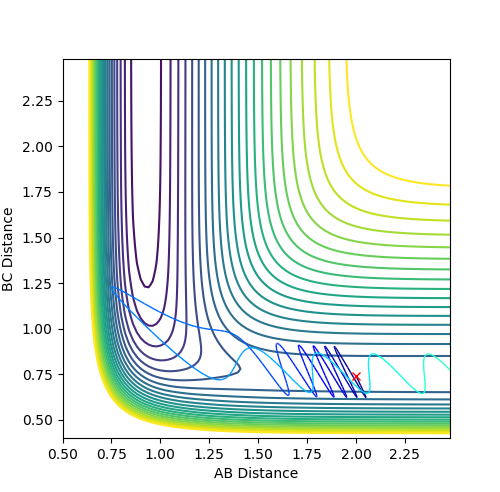
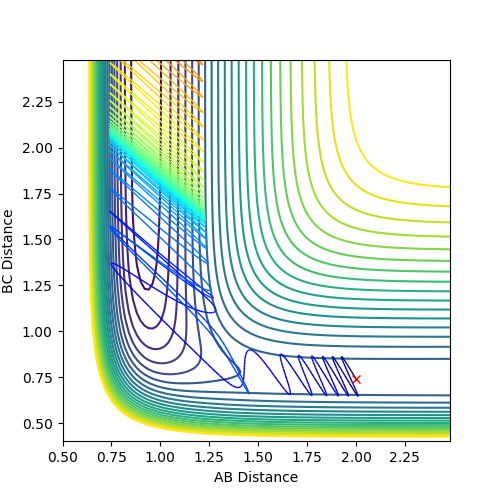
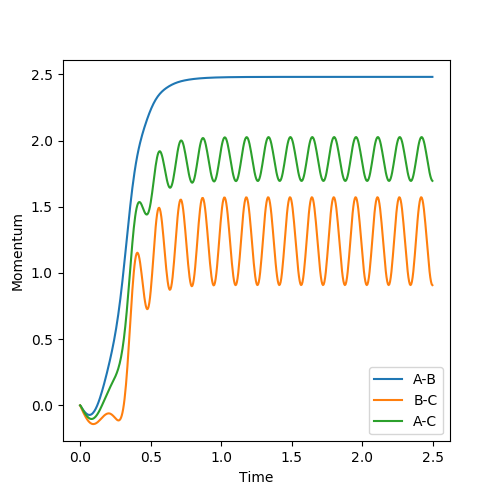
The mep (minimum energy path) trajectory is a smooth line on contour and surface plot (Fig.7 Fig.8) while the trajectory under dynamics calculation is oscillating along the pathway. (Fig.10 Fig.11) The mep trajectory takes more steps and longer time than the dynamics trajectory as shown in internuclear distance against time plots. (Fig. 9 Fig.12) The momentum is zero all the time under mep calculation (Fig.13) but under dynamics calculation, the momenta lines are oscillating against time.

The differences arise from mep and dynamics calculations can be explained by the the natures of the two calculations. Under mep calculation, the atoms are in extremely slow motion and the momentum is zero for each step, i.e. the atoms are "stop" after every step. The pathway under mep calculation is formed by connecting all the minimum energy points of each step and appears as a smooth line. On the other hand, atoms are in continuous motion and the momentum is accumulated after each step, atoms are then oscillating on the potential energy surface along the pathway. The steps are set to 5000 in the mep calculation but are only 500 in the dynamics calculatoin. Since the steps in mep are small, more time is needed to complete the same length on the trajectories.

Mm10114 (talk) 15:50, 29 May 2018 (BST) Very thorough explanation supported by all the necessary figures. It is clear you understand very well the difference.

Reactive and unreactive trajectories 

Question 4ː Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.

For the initial positions r₁ = 0.74 and r₂ = 2.0, run trajectories with the following momenta p₁ and p₂ combinations:

Condition	p1	p2	Total Energy/ kcal mol -1	Reactivity
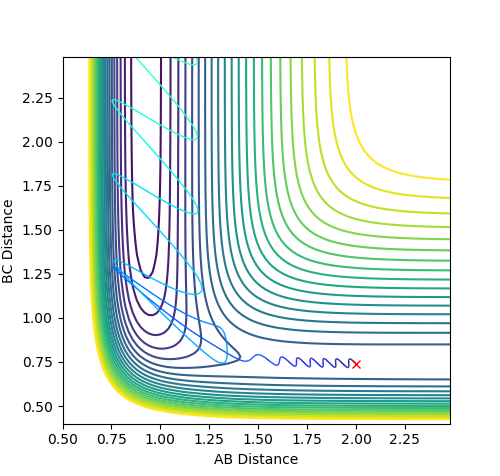
1.	-1.25	-2.5	-99.018	reactive
2.	-1.5	-2.0	-100.456	unreactive
3.	-1.5	-2.5	-98.956	reactive
4.	-2.5	-5.0	-84.956	unreactive
5.	-2.5	-5.2	-83.416	reactive

Condition	Surface Plot	Contour Plot	Description
1.			r2 (BC) decreases when HC approaches bonded HA and HB. The energy processed by the system is sufficient to overcome the activation barrier and crosses the transition state structure to break the HA and HB bond and form a new HB and HC bond. The new bond oscillate as r1 (AB) increases.
2.			HC approaches HB but the energy is insufficient to reach the transition state point, HC then moves further away from the bonded H2 molecule and no new bond is formed. The oscillation along r2 is a result of an increase in momentum p1.
3.			Similarly to condition 1 but with a more negative p1, HA - HB bond oscillates more when r2 decreases. The reaction proceeds and crosses the transition state point to form the products.
4.			Both p1 and p2 are more negative than the previous conditions. The HA - HB bond oscillates vigorously with larger amplitudes. The barrier recrossing happens after the system crosses the transition state region but eventually reverts back to the reactants.
5.			With a slight more negative value of p1 as compared to that in condition 4, the system now processes appropriate energy to proceed to forming products. The vigorous oscillations are resulting from high momenta and barrier recrossing occurs.

Mm10114 (talk) 15:52, 29 May 2018 (BST) So what would be the final conclusion? Does high momenta guarantee a reactive outcome? Otherwise, you did a good job.

Transition State Theory

Question 5ː State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

The main assumptions of Transition State Theory (TST) areː

1. The behaviours of the atomic nuclei follow the classical mechanics rules, i.e. the transition structure is formed as long as atoms or molecules collide with enough energy.

2. The intermediates have a long enough lifetime for the energies to be Boltzmann distributed preceding the next step.

3. The lowest energy saddle point on the potential energy surface is passed over in the reaction system.

The TST does not take into account of the quantum tunnelling effect which allows reactions to happen even when the energy carried by the system is lower than the activation energy barrier, especially for reactions with low energy barriers. Nor does the theory consider the intermediates with short lifetimes. When the energies are not fully distributed, the momentum of the reaction trajectory from the reactants to the intermediate can have effects on product selectivity. Moreover, the theory fails at high temperature because higher vibrational energy modes can be populated for a molecule at high temperature. The molecules can have complex motion and their collisions may result in a higher energy transition structure. The experimental results may thus deviate from that predicted by the TST. For example in condition 4, the kinetic energy of the reactants is much higher than the activation energy required. However, the momenta between atoms are very high and higher vibrational modes are populated that result in higher energy transition structures formed and the system does not pass though the lowest transition saddle point as shown in the diagram. Barrier recrossing occurs but the products are not formed as opposed to the predictions by the TST.

Mm10114 (talk) 15:54, 29 May 2018 (BST) Excellent. You don't forget to reference the source, you link your discussion with observations from previous exercise. Just as it was intended for you to.

EXERCISE 2: F - H - H SYSTEM

Reaction Energetics

Question 6ː Classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

Figure.15 F + H2 position on surface plot	Figure.16 HF and H position on surface plot

The surface plots of the potential energy surface of H + HF → F + H₂ reaction is shown (Fig.15 Fig.16). Distance AB is the distance between H and F atoms and distance BC is the distance between two H atoms. The two minimum points shown in the graph are positions of F + H₂ (Fig.15) and H + HF (Fig.16) respectively. If forward reaction is H + HF → F + H₂, then the backward reaction is F + H₂ → H + HF. As clearly shown in the diagram F + H₂ are at a minimum point of higher potential energy than that of H + HF. Thus, by comparing the potential energy of reactants and products, the signs of changes in enthalpy (ΔH) and the energetics are determined. H + HF → F + H₂ is endothermic and F + H₂ → H + HF is exothermic.

The energetics of the two reactions are in accordance to the predictions by comparing bond strengths of chemical species. The bond energy of H-F bond (565 kJ/mol) is higher than the bond energy of H-H bond (432 kJ/mol). Thus, energy released by forming the H-H bond is not enough to compensate for energy required for breaking the H-F bond and the reaction H + HF → F + H₂ is endothermic. On the contrary, the reaction F + H₂ → H + HF is exothermic.

Transition State Approximation

Question 7ː Locate the approximate position of the transition state.

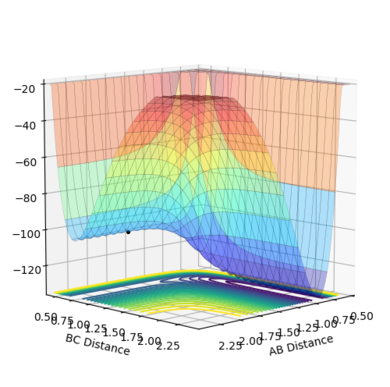
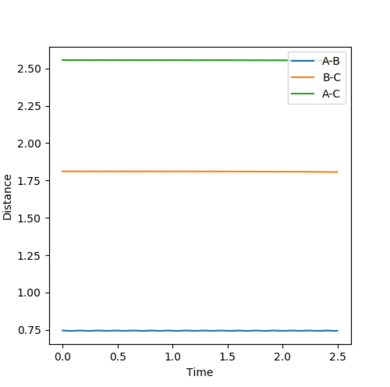
Figure.17 Transition state surface plot	Figure.18 Transition state contour plot	Figure.19 Internuclear distance against time plot (at TS point)

The transition state (TS) is shown as a black dot on the potential energy surface plot (Fig.17) and a red cross on the contour plot. (Fig,18) The position of the TS is at the point where the distance between F and H (r_FH) is 1.810Å and the distance between two H atoms (r_HH) is 0.746Å. The TS is closer to F + H₂ and further away from H + HF. At the transition state position, the distance between F and H, between two H atoms are constant with no momentum as shown in the internuclear distance against time plot as horizontal and flat lines, validating the position is the transition state point (Fig.19)

Mm10114 (talk) 15:55, 29 May 2018 (BST) This is correct. Would be nice if you additionally put 1-2 sentence how you've obtained the TS. What was your approach/sampling technique?

Activation Energies

Question 8ː Report the activation energy for both reactions.

Figure.21 Energy against time plot (HF + H)	Figure.20 Energy against time plot (F + H2)

By performing MEP calculation with slight increase and decrease of the r_FH to 1.820Å to perform F + H₂ → H + HF reaction and to 1.800Å to perform H + HF → F + H₂ reaction, the activation energies (E_a) of both reactions can be calculated from the differences in their potential energies (Fig.20 Fig.21)ː

H + HF → F + H₂ː E_a = -103.751 - (-133.624) = +29.873 kcal mol^-1

F + H₂ → H + HFː E_a = -103.751 - (-103.972) = + 0.221 kcal mol^-1

Reaction Dynamics

Question 9ː In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

Reactionː F + H₂ → H + HF

Initial condition setː r_HF = 2Å r_HH = 0.74Å p_HF = -0.5 p_HH = 0.1

Figure.23 Contour plot	Figure.24 Surface plot	Figure.25 Internuclear momentum against time plot
Figure.26 Animation figure (at the start of the reaction)	Figure.27 Animation figure (at the end of the reaction)

As shown in the plots and animation figures, the H-H bond in the reactants is broken and H-F bond in the products is formed. There are small momenta between both H and F and H-H bond that provide the initial kinetic energy of the reactants and the initial vibrational energy of the H-H bond in the reactants. The initial energy is required to break the H-H bond and reduce the distance of H and F for bond forming and potential energy is released when H-F bond is formed. Since energy is conserved, the reaction energy released is converted to the vibrational energy of the H-F bond and the translational kinetic energies of the products. This is shown in the internuclear momentum against time graph as the initial vibrations of B-C (H-H bond) becomes flat as two H atoms are separated in the product and the A-B (H-F bond) formed in the product vibrates with a large amplitude. (Fig.25) The contour plot and the surface plot also clearly show there is a significant increase in the amplitude of the oscillation of H-F bond which is an indication of the large vibrational energy of H-F bond. (Fig.23 Fig.24)

The predictions can be proved experimentally. The vibrational energy of H-F bond can be determined by measuring the frequency and the intensity of the absorption band of the H-F bond with infrared spectroscopy. The conversion to the kinetic energies of the products can be observed by measuring the temperature of the reaction as the kinetic energy can be converted to thermal energy as products collide with solvent molecules. The temperature is expected to increase as this is an exothermic reaction.

Energy Distribution and Reactivity

Question 10ː Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Condition	rFH /Å	rHH /Å	pFH	pHH
1.	2	0.74	-0.5	-3
2.	2	0.74	-0.5	1.9
3.	2.1	0.74	-0.5	0.1
4.	2	0.74	-0.8	0.1
5.	0.91	2	0.05	-20
6.	0.91	2	0.8	-7.5

Condition	Contour plot	Observation
1.		The products are not formed in the reaction between F and H2 even pHH is very large. Barrier recrossing occurs and the H-H bond oscillates significantly with a large amplitude in the diagram. It should be noted that while keeping pFH to be -0.5 and changing pHH from -3 to 3, the trend is not very obvious as there are many anomalous values of momentum that render the reaction unreactive while slight increase and decrease of momentum make the reaction reactive again. For example, pHH = -0.9 is reactive but pHH = -1.1 is unreactive.
2.		There is reaction between F and H2 and products are formed. The F-H bond formed vibrates significantly along BC trajectory.
3.		There is no reaction under this condition between F and H2. There is not enough energy to cross over the transition state point. Although investigations have shown that there is reaction when rFH is equal or less than 2Å, but there is no reaction when H and F atoms are further apart.
4.		There is reaction between F and H2. By comparison between condition 4 and condition 3, a slight increase in the momentum of F and H which indicates a slight increase in kinetic translational energy result in the formation of products. Investigations have shown that even when rFH is slightly larger than 2Å, the products are still formed. Thus the change in reaction conditions illustrate that the changes in translational energy affect the reactivity the reaction more than the vibrational energy.
5.		There is no reaction between H and HF even though the kinetic translational energy is very high and much higher than the activation energy. (pHF = -20) The trajectory reverts back before reaching the transition state structure.
6.		There is reaction between H and HF. Compared to condition 5, the translational energy decreases significantly while vibrational energy increases slightly. Thus, the vibrational energy is more efficient in promoting the reaction than the translational energy.

The transition state illustrated in Question 7 is closer to F and H₂ than H and HF. From the above illustrations, it can be shown that the translational energy is more efficient in promoting the reaction between F and H₂ which is exothermic, has a lower activation energy and has an earlier transition state. On the other hand, the vibrational energy is more efficient in the reactivity of the reaction between H and HF which is endothermic, has a higher activation energy and has a late transition state. These observations agree with the Polanyi's empirical rules.