MRD:VN314159

H+H₂ system

Minima and transition structures

The gradient of the the potential energy surface tends to infinity when r tends to zero. This means that the potential energy is infinitely large. With r that tends to infinity, the gradient will tend to zero, although the energy will not be at a minimum. This means that there is no bond. Both at a transition structure and a minimum the gradient will be equal to zero. However, the two can be distinguished in the plot from its curvature. A minimum, in fact, has a negative curvature (Fig. 1). A transition structure, however, is a saddle point (a maximum in the minimum energy path), and, therefore, it will have a positive curvature (Fig. 2).

Mm10114 (talk) 16:34, 25 May 2018 (BST) These are all good observation. You only discuss the saddle point in the minimum energy path, what about in the orthogonal direction to that?

Minimum	Transition structure

Figure 1	Figure 2

Locating the transition state

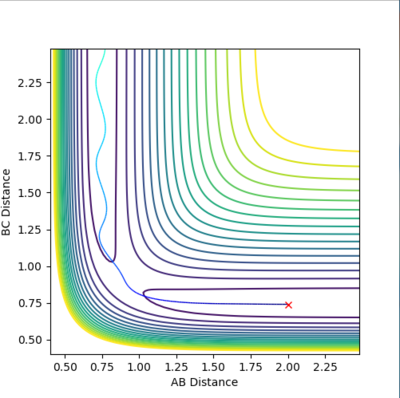
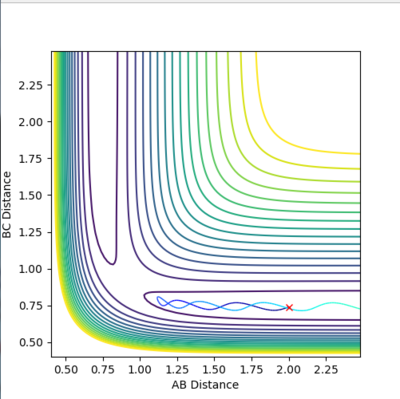
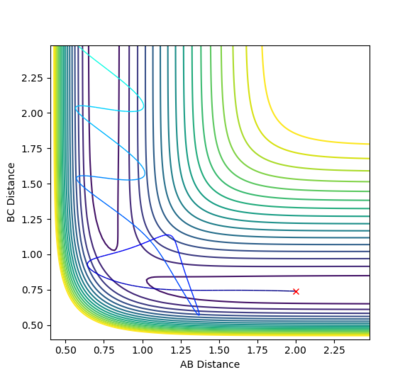
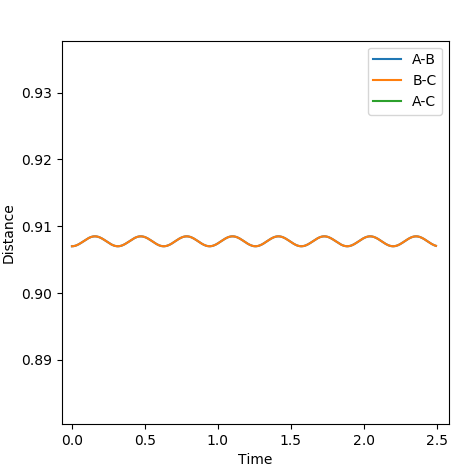
The r_ts can be estimated setting different values of r₁=r₂ and finding the distance that does not lead to the formation of a product (so the distance at which the system oscillates on the saddle point an infinite number of times). The first estimate is based on the H-H bond length in a H₂ molecule, which is 0.74. Using this value in the program, it can be seen that it leads to the formation of a product. Therefore it has to be longer. Increasing it to 0.8, it can be seen that the molecule is still oscillating, although it oscillates at the saddle point. To have a transition state, the potential energy has to be constant, with no oscillations. Trying different values around 0.9, it was found that the minimum oscillation is at 0.907. The Internuclear Distances vs Time plot shows that the oscillations are very small and the distances A-B and B-C) coincide throughout the plot (Fig. 3 and 4).

Mm10114 (talk) 16:42, 25 May 2018 (BST) Nicely explained and supported with plots. Well done.


Figure 3	Figure 4

MEP and reaction path

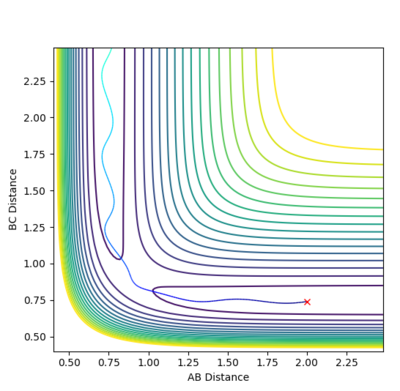
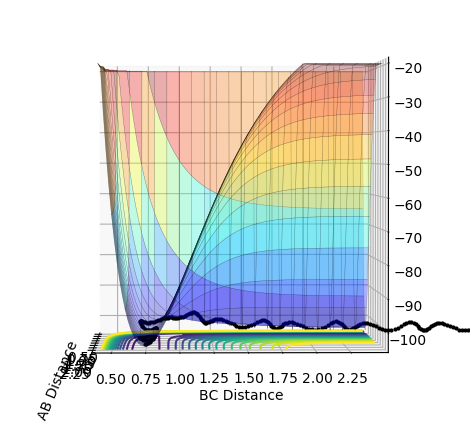
The MEP (calculated with r₁=0.907 and r₂=0.917) indicates just in which direction the reaction will proceed, taking into account just the minima and a velocity that approaches zero in each step. There are no oscillations involved. Also, a high number of steps is needed to understand the reaction trajectory. On the contrary, the oscillation of the system can be seen in a Dynamics calculation, which also has a higher velocity and requires fewer steps. The trajectory highlighted in the MEP shows that the reaction proceeds towards the products. Swapping the values (r₁=0.917 and r₂=0.907) makes the reaction go back to the starting materials.

Mm10114 (talk) 16:42, 25 May 2018 (BST) You correctly observe MEP requires larger number of steps to produce the reaction trajectory of significant length in compare to dynamics calculations, but why exactly is it that way? Worth explaining in more detail using the differences between MEP and dynamics as arguments. Is it the oscillation of the whole system you see in Dynamics calculations? Or do you mean the oscillation of the bond length in the H2 molecule? You should try to state why these oscillations are observed and link it to the velocity.

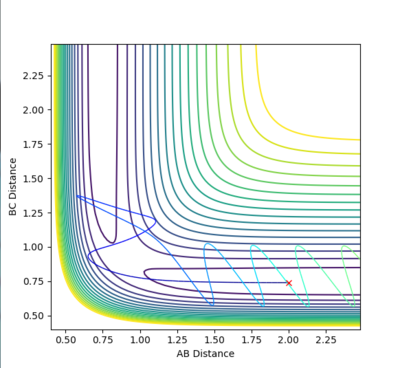
Reactive and unreactive trajectories

p₁	p₂	Total Energy	Reactive?	Description
-1.25	-2.5	-99.119	YES	The transition state is crossed and the reaction goes to completion.
-1.5	-2.0	-100.456	NO	The energy is not sufficient to cross the barrier and the system goes back to the reactants.
-1.5	-2.5	-98.956	YES	The system crosses the transition state and the reaction goes to completion.
-2.5	-5.0	-84.956	NO	The barrier is crossed but the reaction does not go to completion because of barrier recrossing.
-2.5	-5.2	-83.416	YES	Although the barrier is crossed twice (towards the product and then the reactants), it is crossed a third time and the reaction goes to completion but the vibrations of the product are quite intense.

Mm10114 (talk) 16:46, 25 May 2018 (BST) Can you draw conclusions by summarising the observations from the trajectories in the table? The 4th and 5th example both have initial momenta higher than the first three cases, so what does that mean? Is high momenta not always enough for a reaction to occur?

The Transition State Theory (TST) is based mainly on three assumptions:

the nuclei behave according to classical mechanics
an activated complex is in equilibrium with the reactants
if the molecules pass thought the transition state, then it is inevitable that they will form a product (although it is assumed that there is just one product possible)

TST is fundamentally an approximation so it does not always match experimental observations. It does not take into account tunnelling, that allows molecules with a low energy to cross the activation energy barrier and move towards the products. Also, as it can be seen in the fourth example above, sometimes molecules can cross the transition state point and cross it again to return to the reactants. However, TST does not consider barrier recrossing.^[1]

F-H-H system

Note that in each figure A=F, B=H, C=H.

PES inspection

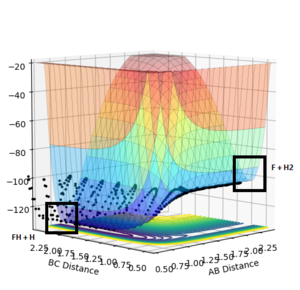
The F + H₂ reaction is exothermic. This is due to the fact that the F-H bond is stronger than the H-H bond and, therefore, the system gains stability (overall). Contrarily, the FH + H reaction is endothermic, because the bond formed (H-H) is less stable than the bond broken (F-H). Breaking this bond requires a considerable energy, because the energy barrier that has to be overcome is high. It can be seen in Fig. 5.

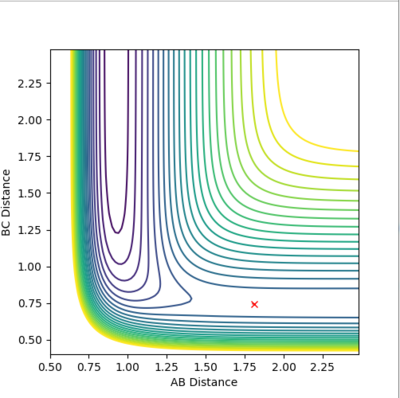
The saddle point, which represents the transition state [F-H-H]‡, can be found with a distance between F-H of 1.81 and between H-H of 0.745, as it can be seen in Fig. 6 and 7.


Figure 6	Figure 7

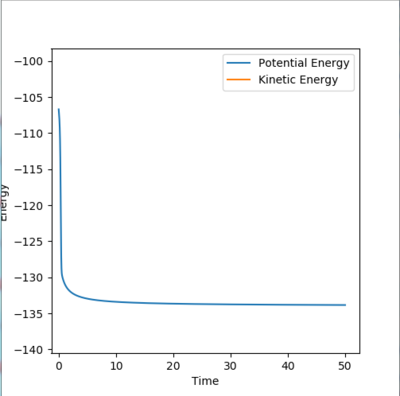
The activation energy for the production of FH + H is 0.158 Kcal/mol and for the production of HH + F 29.884 Kcal/mol. The activation energy was found by performing an MEP in both directions (towards the reactants and the products) from the transition state. Then The energy of the last geometry was found and the difference with the energy of the transition state was calculated.

Mm10114 (talk) 16:50, 25 May 2018 (BST) Are you sure about the unit? Should it not be kcal/mol and not Kcal/mol? Be careful in the future, as science is not indifferent for upper/lower case in units. Yours could be read as Kelvin * calorie / mol instead of kilocalorie / mol. Otherwise you've done a good job.

ENERGIES
HH + F	HF + H	TS
-133.867	-103.916	-103.758

Reaction dynamics

HH + F --> FH + H

The reaction that leads to the production of FH + H is exothermic. Heat is liberated in the reaction. This means that the potential energy is converted to thermal energy, which is vibrational energy. The HF molecule, in fact, vibrates quite vigorously (it has a high momentum). This can be seen in Fig. X. The amplitude of the oscillations is, in fact, quite big. Calorimetry would be a good way of confirming the reaction^[2].

Setting up the calculation with r_HH = 0.74, p_HF = -0.5 and changing the value of p_HH between -3 and 3, it can be noticed that even if the momentum of the H-H bond is positive (bond is elongating), the reaction does not always go to completion because the momentum of the H-F bod, once it is formed, is too big and the bond breaks, forming the H-H bond again. Increasing the F-H momentum (to -0.8) and decreasing the H-H momentum to 0.1, however, the reaction proceeds to completion. This means that increasing the translational energy of the HH - F collision (by increasing the F-H momentum) is more effective than increasing the momentum of the H-H vibration.

Mm10114 (talk) 16:53, 25 May 2018 (BST) Nicely done. Would be even nicer if you didn't forget to update the figure numbers in "Fig. X".

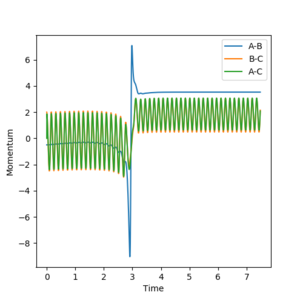
r_HH	r_FH	p_HH	p_FH
0.74	2.3	2	-0.5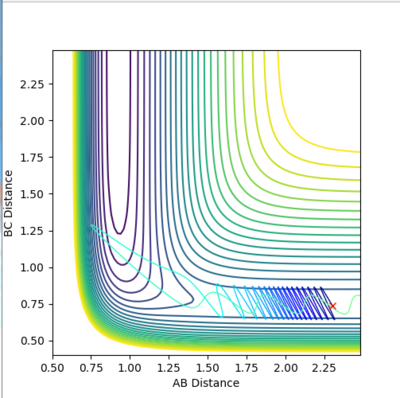
0.74	2.3	-2	-0.5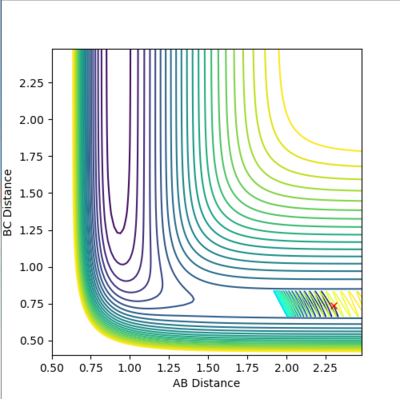
0.74	2.3	0.1	-0.8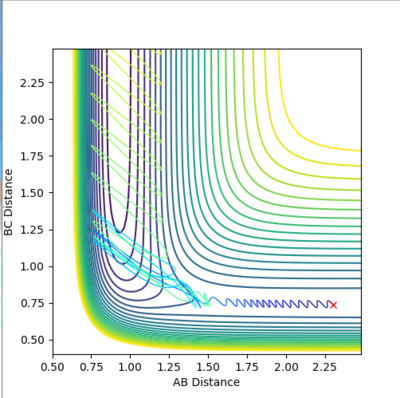

HF + F --> HH + F

This reaction is endothermic and has to overcome a big energy barrier to take place. The momentum necessary to overcome it can be estimated using the inversion of momentum procedure. Starting from the transition state, the system is displaced slightly and the momentum of the system at the bottom of the well (where the products FH and H are formed) is calculated. The momenta obtained are p_HH = -2.3 and p_HF = around -6. Therefore, inverting the sign and increasing the momentum (Fig. X) to overcome the activation energy, a reactive trajectory can be found. It can be noticed how, even having a high translational energy in the FH - H collision, the reaction does not go to completion, whereas having a high F-H vibrational energy causes the bond to break and the products can be formed.

r_HH	r_FH	p_HH	p_FH
2.3	0.74	-1.9	6
2.3	0.74	-2	3
0.74	2.3	-6	3

Polanyi's rules

Polanyi's empirical rules state that a late transition state is easily overcome increasing the vibrational energy, but not with translational energy. On the contrary, an early transition state is overcome with increased translational energy, whereas vibrational energy is not effective^[3]. The two systems here described confirm these empirical rules. In the first reaction there is an early transition state and, even with a high H-H momentum, the reaction almost never goes to completion. When increasing the translational energy, however, it can be seen that the energy barrier can be easily overcome. In the second reaction, the transition state is very late and, having a very high vibrational energy between F and H helps in overcoming the energy barrier.

Mm10114 (talk) 16:54, 25 May 2018 (BST) Good discussion with examples.

References

↑ Atkins, P., & de Paula, J. (2010). Atkins’ Physical Chemistry (10th ed.). Oxford: Oxford University Press.
↑ Thermodynamics course, 1st year, N. Brooks
↑ http://brouard.chem.ox.ac.uk/teaching/dynlectures4to6.pdf

[1] Atkins, P., & de Paula, J. (2010). Atkins’ Physical Chemistry (10th ed.). Oxford: Oxford University Press.

[2] Thermodynamics course, 1st year, N. Brooks

[3] ttp://brouard.chem.ox.ac.uk/teaching/dynlectures4to6.pdf

[1]

[2]

[3]

H+H2 system