MRD:VFC2398

Molecular Dynamics

H + H₂ system

Dynamics from the transition state region

A + B-C -> A-B + C

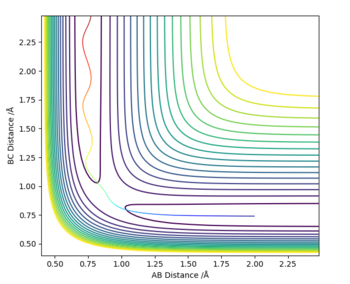
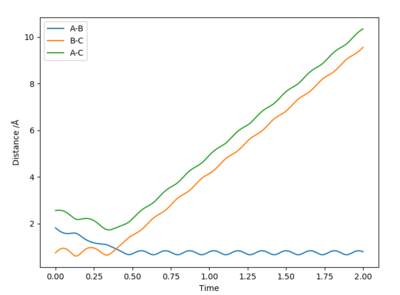
A reactive trajectory can be generated on a potential energy surface measuring the potential energy with respect to the AB and BC inter-atomic distances by applying a set of initial conditions for the positions of the atoms and their momenta. From the potential energy surface the trajectory can be determined by finding the derivate across the whole potential energy surface to find the minima. To find the energy of the transition state, which on the trajectory resembles a saddle point, the derivative of the trajectory must be found but this time to determine the maximum energy. Since the system being observed is symmetric at the maximum ie. transition state, AB and BC inter-atomic distances will be equal as a result can be seen as the point of intersection Figure 1. below of the Internuclear distance against Time graph.

Figure 1. Internuclear Distance vs Time for H + H₂ reaction. R_TS ≈ 0.9107 A

W= ∫F. ds
E= ∫F. ds
de/ds = F

At the minimum of a potential energy curve, the force is zero so the molecule has no potential energy so it is no longer vibrating this results in the AB and BC to have no vibration so the periodic symmetric vibration wave becomes a straight line due to not having an amplitude as a result of the force on the bond being equal to zero. By inserting different values of r₂ (AB)= r₁ (BC) and P(AB)=P(BC) = 0, the transition state bond length can also be determined via trial and error for H + H₂ system.

Good methodology and inclusion of units. Would be nice to see your TS definition, although I can infer one from your explanation above. Mys18 (talk) 17:40, 19 May 2019 (BST)

Trajectories from r₁ = r_ts+δ, r₂ = r_ts

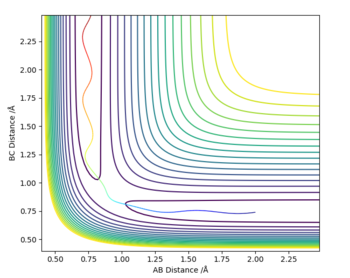
An MEP shows the mean energy path hence no vibration contributions of the molecules can be seen therefore the trajectory that is depicted on the PES is not wavy but straight, it differs from a dynamics calculation as it does not take the gradient of the potential energy of previous steps into account, only the gradient at the current step is accounted for.A dynamic calculation will display changes in momenta whereas in an MEP there are no changes in the momenta of the atoms/molecules.

Quite rightly so, perhaps support your answer by showing your contour plots for MEP and dynamic methods. Why does the MEP method not consider vibrations? - (think about other parameters) Mys18 (talk) 17:45, 19 May 2019 (BST)

Determining reactive trajectories

The following table shows how changing the momenta p₁ (BC) and p₂ (AB) within a set of initial conditions with the inter-atomic distances kept constant r₁ = 2.0 and r₂ = 0.74 can affect the reactivity of a reaction.

p1 (BC)	p2 (AB)	Etot	Reactive?	Trajectory	Description of Dynamics
-1.25	-2.5	-99.018	Yes		A H atom approaches a H2 molecule, the straight line indicates that there is no vibration until the point of collision where a new H2 vibrating molecule is formed.
-1.5	-2.0	-100.456	No		H atom approached a H2 molecule however the energy of the reactants is insufficient to overcome that of the activation energy therefore the product is not formed and the reactants are reformed as it returns to the reactant channel.
-1.5	-2.5	-98.956	Yes		This reaction is successful hence the H atom approaches a H2 molecule with enough energy to overcome the activation energy and form the product H2 molecule.
-2.5	-5.0	-84.956	No		Reactants have enough energy to overcome the activation barrier to the products, in fact an excess of kinetic energy is observed resulting in the activation energy of the backward reaction being overcome hence the reactants are reformed.
-2.5	-5.2	-83.426	Yes		This reaction is successful hence the H atom approaches a H2 molecule with enough energy to overcome the activation energy and form the product H2 molecule.

From this investigation it can be concluded that a reaction is very sensitive to the energy that is supplied to it and that supplying a reaction with enough energy to surpass the activation energy will not necessarily lead to a successful reaction.

Good, and quite rightly ROW 4 justifies your conclusion. Mys18 (talk) 18:03, 19 May 2019 (BST)

Transition State Theory

The Transition State Theory can be used to provide a more accurate measure of the rate constant of a reaction compared to other methods such as the Arrhenius equation. The theory involves treating the transition state as an activated complex in equilibrium with the reactant, therefore the energy of the transition state relative to the reactants determines the E_a of the reaction.¹ The reaction can be considered as the following: A + BC <—> [ABC*] —> AB + C where ABC* represents the transition state complex

The transition state theory was used to determine that the rate of a reaction by looking at the motion through the saddle point of a potential energy surface. The assumptions for this theory include:

-The reactants are in equilibrium with the transition state complex

-The energy of the particles follows a Boltzmann distribution during the reaction

-Once the transition state complex is formed, the structure is not converted back to the reactants.

As a result of these assumptions the rate of reaction would be overestimated as it is unable to to describe the scenario of reactions with enough kinetic energy to reform the reactants from the products.

Excellent, in reality you have computationally proven the reformation of excited reactants. Perhaps something to consider, is the rate also affected if we have either a light or heavy atom? What is a light atom? Mys18 (talk) 18:07, 19 May 2019 (BST)

References

(1) S. J. Moss and C. J. Coady, Potential-Energy Surfaces and Transition-State Theory, University of Aston in Birmingham, Computer Series

F - H - H System

PES Inspection

Literature shows that the H-F bond energy (565kJmol^-1)¹ is greater than that of H-H(462kJmol^-1)¹ hence the enthalpy of dissociation of the H-F molecule is greater, this is concordant with the potential energy surface for the F - H - H system. Figure 1. shows that F + H₂ -> HF + H is an exothermic reaction, the potential energy surface shows the products having a lower energy than the reactants. The backward reaction is HF + H -> H₂ + F and is therefore endothermic, this reaction has a greater activation energy due to the greater bond enthalpy of the HF molecule requiring more energy for its dissociation.

Figure 1. Potential Energy Surface for F-H-H system

Good explanation. From your own knowledge of bonding, why do we already know H-F is a rather strong bond? Mys18 (talk) 18:10, 19 May 2019 (BST)

By using Hammonds Postulate it can be approximated that the transition state will resemble the either the products or the reactants depending on which is closer in energy. Therefore, in the endothermic reaction the transition state will closely resemble the reactants whereas in an exothermic it closely resembles the products. The idea of Hammonds postulate was used in order to identify the inter-atomic distances at the transition state. For the endothermic reaction the known H-H bond length (0.7445 A) was used as the initial condition and the H-F distance was manipulated to determine the location of the transition state using a graph of the Internuclear distance vs Time to find the optimized H-F distance (1.8311 A) where the force of bond equals zero.

MEP calculations were carried out and a plot of the Energy vs Time was used in order to determine the activation energy of the forward and backward reactions.

Figure 2. Energy vs Time plot of endothermic reaction showing E_a

HF + H -> H₂ + F Activation Energy= 29 kcal/mol

Figure 3. Energy vs Time plot of exothermic reaction showing E_a

F + H₂ -> HF + H Activation Energy= 0.2 kcal/mol

Nice inclusion of how you arrived at your answer. Correct units and very good figures! Mys18 (talk) 18:16, 19 May 2019 (BST)

Reaction Dynamics

Reactive trajectory conditions:

R₁(H₂)= 0.74 A

R₂(HF) = 2.30 A

P₁ = -1.7

P₂ = -2.4

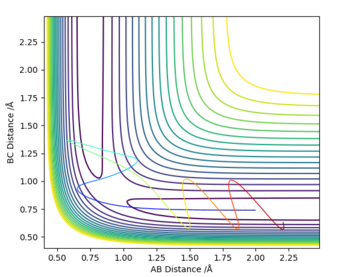
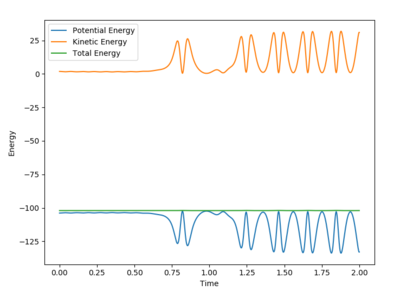
For the reactive trajectory shown in Figures 4 and 5 below of the F + H₂ reaction, it can be seen from the Momenta vs Time graph that there is an interconversion between kinetic and potential energy as a fall in potential energy energy is opposed by a rise in kinetic energy, this is in concordance with the law of the conservation of energy. Therefore, for this exothermic reaction the potential energy is converted into kinetic energy giving rise to vibrations of the HF bond that this formed. Infrared spectroscopy can be used to confirm the conversion of energy by calculating the frequency of absorption of the bond.

Good understanding! Mys18 (talk) 18:19, 19 May 2019 (BST)

Figure 4. Contour Plot of F + H₂ reactive trajectory

Figure 5. Energy vs Time of F + H₂ reactive trajectory

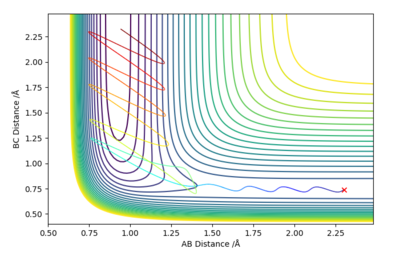
An investigation into the reaction trajectories was conducted using the initial set of conditions listed below, P₂ = -0.5 was kept constant whereas P₁ was varied within the range X= -3 to 3.

R₁(H₂)= 0.74 A

R₂(HF) = 2.30 A

P₁ = X

P₂ = -0.5

R1(H2)	R2(HF)	P2	P1	Contour plot of trajectory
0.74	2.3	-0.5	-2.7
0.74	2.3	-0.5	-2.1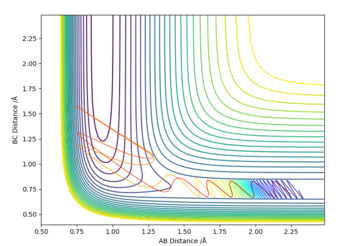
0.74	2.3	-0.5	0.6
0.74	2.3	-0.5	1.6
0.74	2.3	-0.5	2.8	|

The dynamic calculations show that setting P₂ = -0.5 resulted in the reaction being successful at the extremes of the P₁ X range, where when the P₁ was set close to zero the product was not formed and the momentum was insufficient.

Good. Mys18 (talk) 18:23, 19 May 2019 (BST)

Polanyi's Rules

Polanyi's rules state that vibrational energy is more efficient in promoting an endothermic reaction(transition state resembles products) whereas translational energy is more efficient at promoting an exothermic reaction (transition state resembles the reactants).² For the F-H-H system these rules would suggest that F + H₂ -> HF + H being an exothermic reaction has an early transition state and therefore in order for the reaction to be successful translational energy is favoured. This suggests that the vibrational energy of H₂ should be low and experience a lower momentum in order for the trajectory to be reactive.

Perfect! Overall, a well structured report, all questions have been answered with relevant supporting explanations. Your report shows an appreciation of your understanding within this area and you made good use of literature, good job! :) Mys18 (talk) 18:32, 19 May 2019 (BST)

References

(1). Huheey, pps. A-21 to A-34; T.L. Cottrell, "The Strengths of Chemical Bonds," 2nd ed., Butterworths, London, 1958; B. deB. Darwent, "National Standard Reference Data Series," National Bureau of Standards, No. 31, Washington, DC, 1970; S.W. Benson, J. Chem. Educ., 42, 502 (1965).

(2.) Polanyi, J. C. Concepts in Reaction Dynamics Acc. Chem. Res. 1972, 5, 161– 168