MRD:SamGubbins01345038

Exercise 1ː H + H₂ System

Dynamics of The Transition state

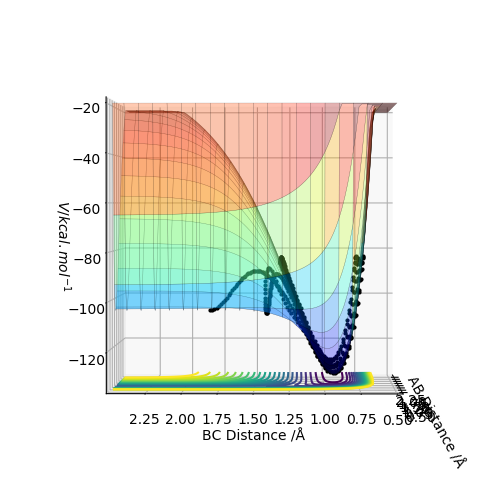
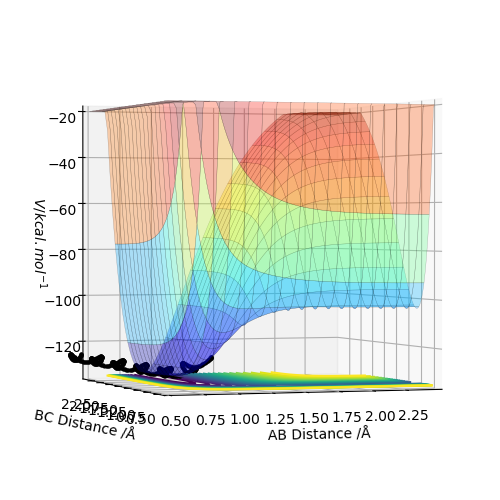
The transition state in a collision reaction between a single atom and a diatomic molecule all comprised of the same element (e.g Hydrogen), is the maximum energy point on the minimum energy path between the reactants and products

This can be seen in figure 1, where the black line shows the lowest energy path from reactants to products and the transition state is the maximum point on this line.

Figure 1ː A Surface Plot showing the path of lowest energy from reactants to products, where the transition state is the maximum of this path.

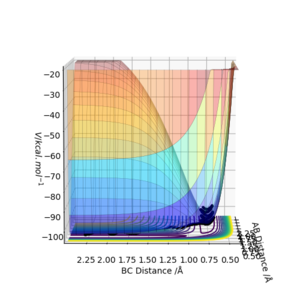
A Mathematical View

Defining the transition state mathematically requires the use of differentiation. Using the surface, the transition state is the point at which the gradient of the potential is zero. This can be seen mathematically asː ∂V(r_i)/∂r_i=0 (1) In the case of a surface, there are two distance variablesː r_AB and r_BC. The requirement for a point to be a stationary point on the surface is thusː ∂V(r_AB)/∂r_AB=0 & ∂V(r_BC)/∂r_BC=0 (2) Fulfilling these requirements generates a minimum energy line. From here, differentiating again, as seen in equation 3, it is possible to locate the stationary points on the minimum energy line. In this case there should be two minima (reactants and products) and 1 maxima (transition state). To distinguish between them, differentiation is used again on the points previously determined to be stationary on the minimum energy line. As we're searching for a maxima, the third order differential should be a value lower than zero. This can be seen mathematically in equation 4.

∂²V(r_i)/∂r_i²=0 (3).

∂³V(r_i)/∂r_i³<0 (4)

Good.Sw2711 (talk) 12:36, 16 May 2019 (BST)

Locating the transition State

At the exact point of the transition state maxima, a trajectory could be set, and with no initial momentum, it will remain there forever. This is equivalent to balancing a ball on a point from which it doesn't move. However, if the geometry is changed only slightly, the trajectory would move towards either the reactants or products, as a ball would down a hill. In turn, to locate the maxima and hence the transition state exactly, it is possible to start trajectories near its exact value and see if they point towards to reactants or products, and adjust accordingly. Using the internuclear distance vs time plot, it is possible to estimate the transition state's position r_ts.

I estimated that the position was roughly 0.9 angstroms, and this produced figure 2. By zooming in it was clearly an average position of about 0.908 angstroms, seen in figure 3. Finally as seen in figure 4, it was around 0.9075 angstroms. This produced figure 4 and gave me a satisfactory rough estimate for r_ts.

Figure 2.

Figure 3.

Figure 4.

Figure 5.

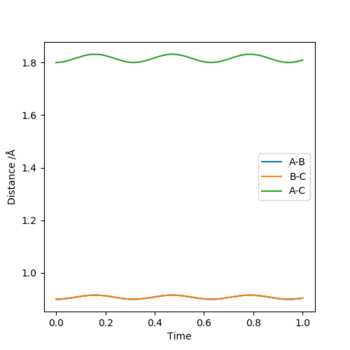
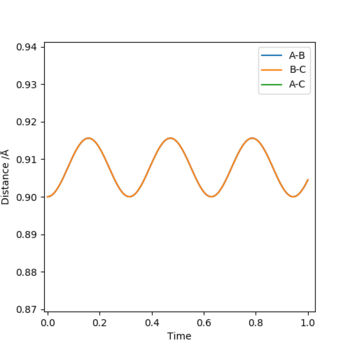
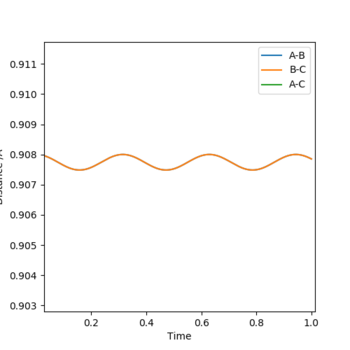
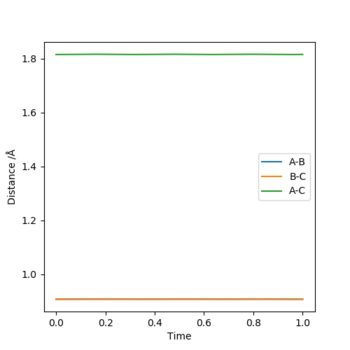
Figure 5 shows the non-zoomed internuclear distance vs time plot where the orange curve is roughly flat, and has a Y value of 0.9075 angstroms- my estimate for the transition state's position.

Good.Sw2711 (talk) 12:36, 16 May 2019 (BST)

Calculating the reaction path

Next, the calculation type was changed. Having found the transition state, I set the AB distance to 0.9085- which is r_ts̟0.01. I then ran an MEP (minimum energy path) calculation. The momenta of the diatomic and the atom were both set to 0. As can be seen in figure 6, this produced a trajectory that simply followed the valley floor from one local minimum (reactant) to the local maximum at the transition state.

Figure 6ː The MEP path between the two nearest stationary points on the minimum energy path.

This path is special in the fact it represents infinitely slow motion so that in each time step the molecules' vibrations and velocities are reset to 0.

I then changed the calculation type back to dynamics and ran the calculation under the same conditions. This produced a similar trajectory to the MEP, but there are a few differences. Firstly, the line was not straight, and had sideways motion like a snake. This is because now that the motion is not infinitely slow, the molecules can vibrate hence creating this sideways motion of the line. Also, the length of the line has increased beyond the scope of the surface plot. As the dynamics calculation will not stop at all stationary points unless instructed too, it does not end at the minimum point that is the reactants or products and continues beyond this. This can be seen in figure 7.

Good observationSw2711 (talk) 12:37, 16 May 2019 (BST)

Figure 7ː The Dynamics calculation that was compared to the MEP path in figure 6.

Reactive and Unreactive Trajectories

The following table shows a multitude of different conditions of momentum for each p₁̟ and p₂̟ where r_AB̟ and r_BC̟ are set to 0.74 and 2.0 respectively.

P1	P2	Etot	Reactive?	Description of the Dynamics
-1.25	-2.5	-99.02	Yes	Smooth reaction where the transfer of a hydrogen atom is seamless and the minimum energy path is roughly followed.
-1.5	-2.0	-100.45	No	Momentum not enough to get the reaction energy over the activation energy barrier so the result is a bouncing off of one another effect where the reactants remain unchanged.
-1.5	-2.5	-98.96	Yes	Atom B(middle of collision) begins to dissociate from atom A before the collision. It then meets atom C and bonds with it leading to a successful reaction.
-2.5	-5.0	-84.89 BUT Varies initially	No	Both molecules have high momentum. When the collision occurs, the activation energy is initially reached and the transition state is overcome. However, due to the elastic nature of the reaction, a second collision occurs where the reaction is reversed and the reactants are formed again, so the energy path goes back over the transition state and back to the initial conditions. What do you mean by 'the elastic nature of the reaction'?.Sw2711 (talk) 12:57, 16 May 2019 (BST)
-2.5	-5.2	-83.40	Yes	Similar to the above. However, this time there is enough momentum to overcome the initial energy barrier, Do you mean the previous reaction doesn't have enough momentum? It clearly does! It just bounced back. You have other examples with less momentum but the reaction still went through. Why? .Sw2711 (talk) 12:57, 16 May 2019 (BST) and then to overcome the second one where the bounce back happened in the above. Therefore a double collision where it then goes back over the transition state again occurs, and the products are formed.

Conclusions from the table

The table shows that just increasing the momentum of the particle and the molecule individually doesn't necessarily mean the reaction will take place. There are specific combinations in which the reaction will take place and if the momenta of the two species are too close then a collision is more likely to lead to a elastic bouncing off effect. However, if the momentum of one of the species is greater by a specific proportion than the other species, then a successful collision will occur, leading to products. Also, this means that the total energy of the reaction is not instrumental in deciding whether or not a reaction occurs, as seen by the total energy figures in the table. It can be said that the rate of the reaction would be predicted to be lower in experiment than theory due to the re-crossing of the system back over the transition state to the reactants, hence lowering the actual rate constant.

Fair discussion.Sw2711 (talk) 12:57, 16 May 2019 (BST)

Transition State theory

There are three assumptions made by the transition state theory determining whether or not the reaction will take place. They areː 1. Reactants are in constant equilibrium with the transition state structure 2. The energy of the particles follows a Boltzmann distribution 3. Once the reactants become the transition state, the transition state does not collapse back into the reactants. Comparing to the results I obtained, there are a few discrepancies. Assumption three states that the reactants will not collapse back into themselves once they've reached the transition state. However, as seen in the table this is not always true. There are two occasions that when the momentum is high enough, barrier recrossing occurs, whether or not they lead to a successful reaction is irrelevant. Good, now what do you think assumptions 1 & 2?.Sw2711 (talk) 12:57, 16 May 2019 (BST)

Exercise 2ː F-H-H System

PES Inspection

This part is good.Sw2711 (talk) 12:59, 16 May 2019 (BST) Firstly, for H₂ + F, the distance between A and B (H-H) was again set to 0.74, and the B-C (H-F) distance as set at 1.81. From here, different momenta values were trialled until a reaction pathway that crossed over the transition state was found. Plotting the surface of the reaction as seen below, it can be seen that the reaction pathway as a whole slopes downward, and is hence and exothermic reaction as the products are lower in energy than the reactants. As the H-F bond dissociation energy is higher (569 kJ/Mol) than the H-H bond dissociation energy (436 kJ/Mol), it can be said that the H-F bond is stronger. In turn this is a favourable reaction as a stronger bond is formed.

Next, the reaction H + F₂ was trialled, using B-C (H-F) as 1, with the H-F bond length was changed too 1 also. By creating a surface plot, it was possible to see that this reaction is endothermic. This is because, as seen below, the products' energy is higher than the reactants' energy. Therefore, the Gibbs free energy change of reaction is positive and thus it is endothermic. This also means that the reaction is not spontaneous. This is qualitatively explained by the fact that the H-F (reactant) bond is stronger than the H-H (product) bond, hence energy must be put into the system for a reaction to take place.

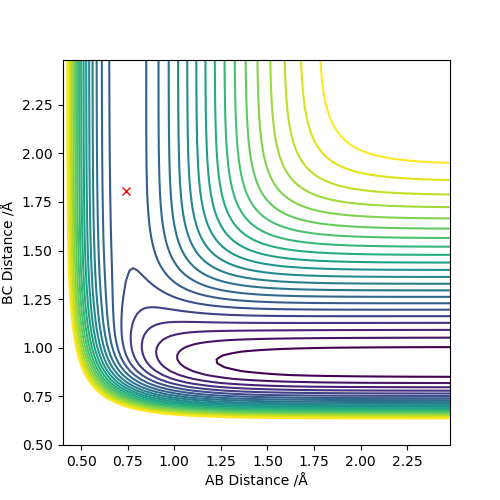
Next, it was possible to locate the transition state. As the reactions are related by being the reverse of one another, they have the same transition state. This was found by moving the internuclear distances until the ball no longer rolled. The atoms are no longer homonuclear as they were in the hydrogen example and therefore the separation between H-H and F will not be equal. TSː H-H 0.74, H-F 1.808 where H-H = A-B and H-F = B-C. This can be seen from the contour plot below as the trajectory does not move from its initial position when the plot is allowed to update. To further back this up, an internuclear distance vs time plot (see below) shows that the is no deviation in any inter-atomic distances allowing the conclusion that we're at the transition state.

Finding the activation energy of the reaction

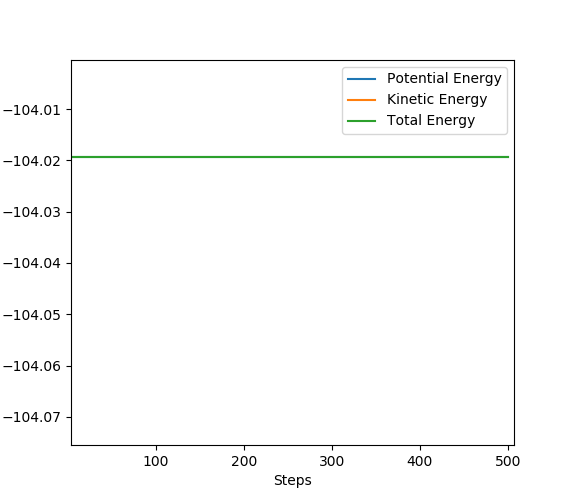
This part is also very good.Sw2711 (talk) 13:11, 16 May 2019 (BST) Now that the transition state has been located, it's energy can also be known. By looking at an energy vs time plot (below) the total energy of the TS is found to be -103.75.

To determine the activation energy, the energy of the reactants is also needed. Therefore for the exothermic H-H F reaction, I set the separation of the molecule and the fluorine atom to 5 which meant there was no interaction between them, in turn the total energy would give the total energy of the reactants, and this was determined to be -104.019 (see below). The activation energy is the difference between these two, hence isː 0.27.

Just don't forget the units. Should be kcal/mol.Sw2711 (talk) 13:11, 16 May 2019 (BST)

For the endothermic reaction, the activation energy is much higher as the HF bond dissociation energy is greater than the HH bond dissociation energy. The same process as above was taken as the transition state energy is the same due to it being the same species, and therefore on the energy of the reactants was left to be found. As seen below, this total energy was determined to be -134.02. Therefore the overall activation energy for this reaction was calculated to beː 30.27.

Reaction Dynamics

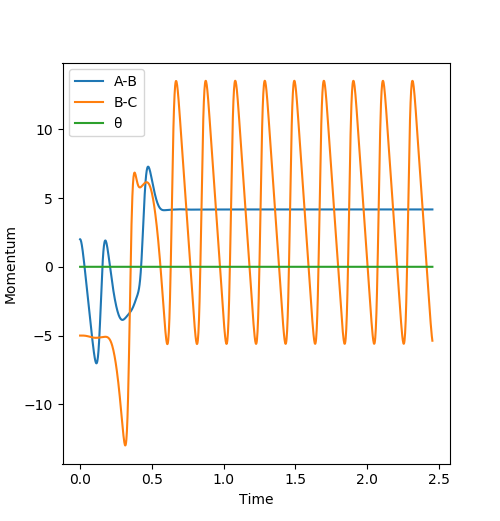
When HH and F react, there is a lot of translational energy before the collision takes place, and little vibrational energy. However, when the collision occurs, a lot of translational energy is converted into vibrational energy so the HF molecule formed continues to vibrate after the collision has occurs, and moves off more slowly so there is less translational energy. The energy before and after the collision must be the same since total energy is conserved so therefore the gain in vibrational energy is matched by an equal decrease in translational energy. This increase can be seen by the BC (HF) momentum vs time curve which is orange on the figure below. To measure this experimentally, bomb calorimetry would be used. This is a good method as it is the standard way of measuring reaction energies that are not in solution, and is ideal for gases and can withstand high pressures, which are necessary for the reverse reaction due to its high activation energy due to the large bond dissociation energy of the HF bond.

You've clearly noticed the change between translational energy and vibrational energy. But they are both kinetic energy. Where is the potential energy? .Sw2711 (talk) 13:14, 16 May 2019 (BST)

Polanyi's Rules

This part is also very good.Sw2711 (talk) 13:15, 16 May 2019 (BST) Polanyi's rules state that a vibrational energy is better for overcoming a late transition state (endothermic) and that translational energy is better for overcoming an early transition state (exothermic) . For the F and HH reaction, with the conditions specified in the script set, HH momentum was adjusted for values between -3 and 3. As momentum was increased in either direction, the reaction became less successful. This agrees with Polanyi's rules because as momentum's absolute value is increased, the vibrational level of energy is increasing. Therefore, as this reaction is exothermic, the likelihood of a successful collision decreases according to Polanyi's rules. However, an anomaly was found. At HH momentum of 2.9, which has high vibrational energy, the exothermic reaction does occur, contrary to Polanyi's rules. This figure is shown below.

Following this, an attempt was made to get the reverse reaction to occur. Knowing it was endothermic, Polanyi's rules suggest that vibrational energy would be most useful for overcoming what is a large barrier. Due to the strength of the HF bond, a large amount of energy is required. After a long list of conditions, it was found that by setting the HF momentum to -10, it was possible to overcome the high activation energy, even if starting at the bottom of the entry well. This is shown in the figure below. To conclude, in terms of reaction efficiency, it is more optimal to have majority translational energy when there is an early transition state (exothermic) and it is better to have majority vibrational energy when there is a late transition state (endothermic). This is epitomised by the above reactions and characterised by their bond strengths.