MRD:SMYM

5/5 - An excellent report overall. Well done!

Exercise 1: H + H₂ system

Transition state on an energy potential diagram

( "On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?" )

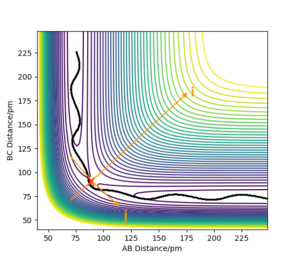
On a potential energy surface plot, the transition state is the maximum on the minimum energy pathway which links the reactant and product. Such a point is also referred to as a saddle point. The minimum energy pathway is portrayed in Figure 1, with the saddle point marked with 'X'.

With the transition state being a stationary point, the derivative with respect to each coordinate must equal to zero.

$$\begin{gathered} \frac{\partial V(r_1)}{\partial r_1} \\ =\frac{\partial V(r_2)}{\partial r_2} \\ =0 \end{gathered}$$ , where $V$ is the potential energy, $r_1$ is the AB distance, and $r_2$ is the BC distance.

Mathematically, a saddle point on a surface plot is a local minimum in one direction but a local maximum in the orthogonal direction. Diagonal vectors relative to $r_1$ and $r_2$ can be set up (see Figure 2) so that the transition state is a maximum along $j$ and a minimum along $i$:

$\frac{{\partial }^{2}V}{\partial j^2}<0$ , $\frac{{\partial }^{2}V}{\partial i^2}>0$

Figure 1. A potential energy surface plot showing the minimum energy path. The transition state is marked with 'X'.

Figure 2. Potential energy contour plot with coordinates i and j defined.

EXCELLENT!

Locating the transition state

( "Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory." )

The following two statements of the transition state must be true:

1. The transition state is a maximum on the minimum energy pathway, which means that moving away from the transition state will result in a steep decrease in potential energy. If the reactants begin at the transition state and are given zero momentum, they will remain there, giving no trajectories.
2. Since the potential energy surface plot is symmetrical for the H + H₂ system, r₁ must equal r₂ at the transition state.

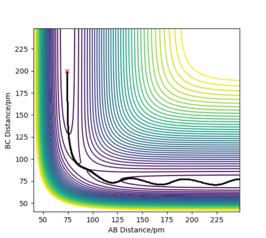
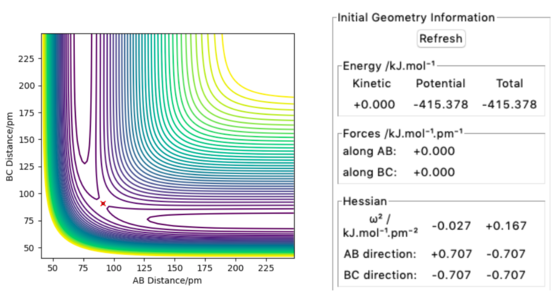
Utilizing the above statements, the transition state can be found by setting r₁ = r₂, and p₁ = p₂ = 0. The transition state would be successfully located if no trajectory is shown, and forces along AB and BC direction equal zero. After fine-tuning the decimal places to F = 0 , the transition state is found to be at 90.7742 pm. The contour plot and the energy and forces outputs are shown in Figure 3.

Good!

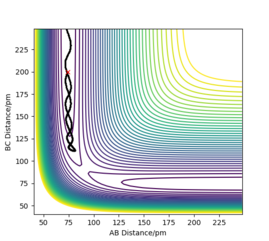
The finding of the transition state at 90.7742 pm is also supported by the internuclear distances versus time plot (Figure 4)as two straight lines are shown, showing a constant internuclear distance at all times. When the reactants are not at the transition state, the internuclear distances show as two oscillating lines due to the asymmetrical vibrations of the two reactants. When the transition state is approached, the molecules achieve symmetrical vibrations.

Figure 3. Contour plot of the transition state with the energy and forces outputs

Figure 4. Internuclear distances vs. time plot of the transition state

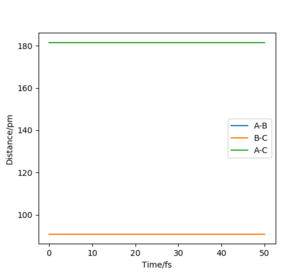
Good!

Reaction path calculation with MEP and Dynamics

( "Comment on how the mep and the trajectory you just calculated differ." )

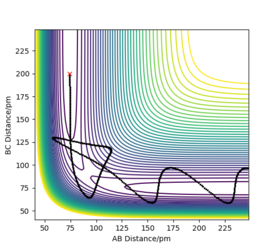
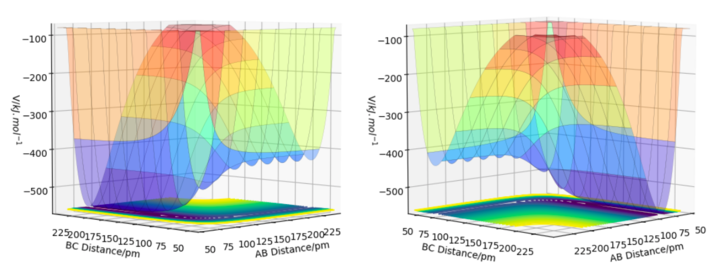
To calculate the reaction path, r₁ was set as 91.7742 pm, and r₂ was set as 90.7742 pm, both momentums were equal to zero. The contour plot of the trajectories for both MEP and dynamic simulations are displayed in Figure 5.

Figure 6. The dynamic calculation (left) and the MEP calculation (right) of the path

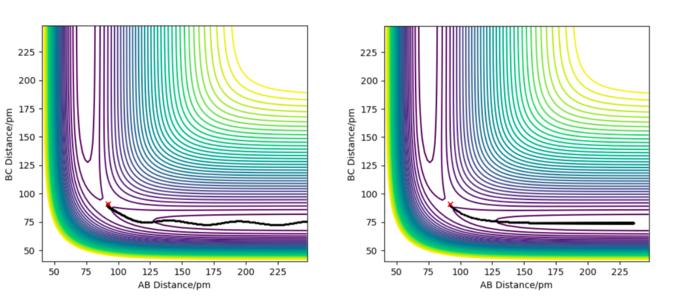
The minimum energy path (MEP) is the path on the potential energy surface with the lowest energy, hence the blackline traces the valley floor in the MEP graph (right of Fig. 6). The reaction path is straight, indicating that there is no vibration of the atoms. This is the case because for each step of the MEP, the momentum is reset to zero, resulting in an infinitesimally low-speed trajectory. There is no remaining inertia for the atoms to 'roll up' the potential energy surface, leading to no oscillation. Although useful for characterizing the reaction, the MEP does not reflect motion of the atoms in reality as their masses have been ignored. On the other hand, vibrations along the minimum energy pathway are seen in the dynamics calculation (left of Fig. 6). The inertia of the atoms are retained in this calculation, allowing enough momentum for the atoms to reach a higher potential on the valley surface.

Excellent!

Reactive and unreactive trajectories

( "Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?" )

The following trajectories were carried out with the initial positions of r₁ = 74 pm and r₂ = 200 pm

p1/ g.mol-1.pm.fs-1	p2/ g.mol-1.pm.fs-1	Etot	Reactive?	Description of the dynamics	Illustration of the trajectory
-2.56	-5.1	-414.280	Yes	Initially, the trajectory shows no H a - Hb bond vibration. Ha - Hb and Hc then overcome the transition state with enough momentum such that the newly formed H b - Hc vibrates.
-3.1	-4.1	-420.077	No	H a - Hb bond vibration could be seen at the start of the trajectory due to increased p1, but this trajectory does not arrive at the transition state due to the decreased p2. The decreased momentum between Hb and Hc resulted in lower kinetic energy when the two collided, and thus Hc is repelled by Hb and not enough energy was present to overcome the potential energy barrier.
-3.1	-5.1	-413.977	Yes	This trajectory is similar to the first example in the sense that it successfully overcomes the energy barrier at the transition state, and the H b - Hc bond formed vibrates in a similar fashion as example one. The only difference is that now there is Ha - Hb bond vibration at the start of the reaction due to the increase of p1. Unlike example two, Hc has enough kinetic energy to collide with H a - Hb due to the increased p2.
-5.1	-10.1	-357.277	No	This reaction has approximately twice the momentum of the first example. Ha - Hb and Hc collide with lots of kinetic energy but the reaction is unsuccessful. Straight after the collision, Ha - Hb bond stretches and Hb - Hc forms. However, the very strong vibration of Hb - Hc causes the bond to break. Ha - Hb is reformed again.
-5.1	-10.6	-349.477	Yes	Here, the reactants again have high momentum and collide with lots of kinetic energy. Similarly, Hb - Hc momentarily breaks due to the strong bond vibration and Ha - Hb reform. However, the vibration between Ha - Hb is so strong that Hb is ejected to Hc, once again forming Hb - Hc. This step pushes the molecules over the transition state and the products are formed. Due to the high momentum, there are strong vibrations between the newly formed Hb - Hc.

In conclusion, having enough kinetic energy during the collision is not the main factor for a successful collision, as the high kinetic energy can cause excessive vibration which breaks the newly formed bond. The molecules must have the right combination of momentum and kinetic energy that leads them onto a successful trajectory.

Transition state theory

( "Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?" )

Transition state makes two crucial assumptions that influence the difference between the observed reaction rate and the observed one:

1. All molecules which possess the necessary kinetic energy to overcome the activation energy barrier will react and become products.
2. No quantum effects are observed.

The first assumption leads to a significant overestimation of the reaction rate as in reality molecules that possess the necessary energy to overcome the activation energy barrier often do in fact not form products. This can be seen above in the reaction in which although the molecules possess enough energy to overcome the barrier, the internal bond vibrations are so strong that no products are formed.

The second assumption causes a slight underestimation of the reaction rate. If quantum effects are considered, tunneling becomes significant. This is especially true for protons as they are light and have a tendency to tunnel. The tunneling effect is observed when a reactant molecule does not have enough kinetic energy to overcome the activation energy barrier but still forms the product. This can be explained by the molecule not going over the activation energy barrier but travels through the potential energy surface.

To summarise, the reaction rates predicted by the transition state theory causes significant overestimations compared to the observed ones. You're correct, but why, given you have two effects acting in opposite directions.

EXERCISE 2: F - H - H system

PES inspection

( "By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?" )

Figure 7. Potential energy surface plots for (left) HF + H --> H2 + F and (right) H2 + F --> HF + F

The valley floor of Figure 7 indicates that H₂ and F are higher in energy than H and HF. This means that when H and HF are converted to H₂ and F, more energy is put in to break the H-F than the energy released from the formation of H-H, making the reaction endothermic. Vice versa, the conversion from H₂ and F to H and HF would be exothermic. This information indicates that H-F bond is stronger than H-H bond. This can be proven by their bond dissociation energy. H-F has a higher bond dissociation energy of 568.6 kJ/mol compared to H-H (436.002 kJ/mol).

Figure 8. The transition state location of the F-H-H system

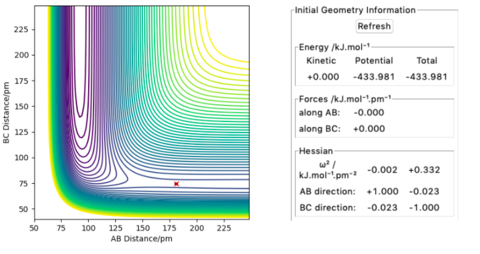
Locating the transition state

The approximate transition state position was found by varying r₁ and r₂ with p₁ = p₂ = 0, until the forces along AB and BC equal to zero. Unlike the H + H₂ system, the potential energy surface is not symmetrical so r₁ will not be equal to r₂ at the transition state.

After fine-tuning, the transition state was found to be at r₁ = 180.855 pm and r₂ = 74.493 pm, where the kinetic energy and the forces acting on the atoms equal to zero (Figure 8).

The activation energy for both reactions

The activation energy could be obtained by looking at the energy difference between the reactants and the transition state. According to Figure 8, the energy of the transition state was -433.981 kJ/mol. To find the energy of the reactants, r₁ is set as the local minimum of the reactant which is the bond length of either HF or H₂. r₂ is then given a large value such that reactant 2 is far away from reactant 1 where there is no interaction between the two and the momentums were set to zero.

H₂ + F --> HF + H:

Atom A = H, Atom B = H, Atom C = F, r₁ = 74 pm , r₂ = 1000 pm The energy calculated for the reactants were -435.100 kJ/mol, which results in the activation energy of 1.119 kJ/mol.

HF + H --> H₂ + F:

Atom A = H, Atom B = H, Atom C = F, r₁ = 91 pm , r₂ = 1000 pm The energy calculated for the reactants were -560.404 kJ/mol, which results in the activation energy of 126.423 kJ/mol.

Good TS estimate and good Ea values. Well done!

Reaction dynamics

Figure 9. Momentum vs. time plot of the reaction H2 + F --> HF + H

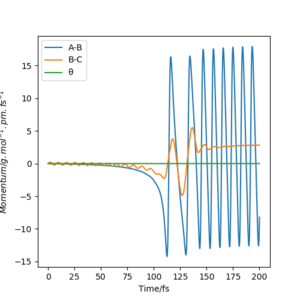
( "In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally." )

A momentum versus time graph of a successful reaction trajectory is shown in Figure 9. For such a trajectory, r₁ was set to 179 pm and r₂ was set to 74 pm, both momentum were equal to zero. The reaction between H₂ and F is exothermic and since the energy is conserved, the products must show an elevation in energy. This can be seen in the strong oscillation of the momentum A-B (the H-F bond), which demonstrates that a large part of the energy is transformed into the vibrational energy of the H-F bond. Apart from that, constant momentum is observed between B-C. This suggests that the H atom is traveling in a constant velocity away from the H-F molecule and so there is a gain of translational energy. The energy released from the reaction as translational and vibrational energy can be measured in the form of heat. One of the measurement technique is by using a bomb calorimeter. The bomb calorimeter is an isolated reaction vessel surrounded by a jacket of water. The change in temperature of the water is measured and with the known heat capacity of the bomb calorimeter material and water, the heat released by the reaction, and therefore the energy can be calculated. However, the bomb calorimeter cannot distinguish between translational and vibrational energies.

A better alternative would be to use infrared chemiluminescence. If during the reaction the energy is mostly converted to vibrational energy, the molecule is going to be in a high energy vibrational state. The molecule will then decay into lower vibrational energy states and emit photons while doing so. These photons can be measured, and if a high amount of photons is detected, most of the energy released during the reaction is in the form of vibrational energy. On the other hand the absence indicates that most of the energy is converted into translation energy.

Good!

Polanyi's empirical rule

( "Discuss how the distribution of energy between different modes (translation and vibration) affects the efficiency of the reaction, and how this is influenced by the position of the transition state." )

The Polanyi's empirical rule states that vibrational energy is more effective at promoting reactions with a late transition state (endothermic reactions), whereas translational energy is more effective at promoting reactions with an early transition state (exothermic reactions).

H2 + F

A series of simulations were carried out to determine the empirical rules. The initial conditions were set as r_HH = 74 pm and r_HF = 220 pm, with p_HF kept at -1.0 g mol^-1 pm fs^-1 and p_HH varied between -6.1 to 6.1 g mol^-1 pm fs^-1.

Reaction No.	pHH/ g.mol-1.pm.fs-1	pHF/ g.mol-1.pm.fs-1	Etot	Reactive?
1	-6.0	-1.0	-403.893	No
2	-4.0	-1.0	-421.893	Yes
3	-2.0	-1.0	-431.893	No
4	0	-1.0	-433.893	No
5	2.0	-1.0	-427.893	No
6	4.0	-1.0	-413.893	Yes
7	6.0	-1.0	-391.893	No
8	-1.6	0.2	-432.774	Yes

In these reactions, p_HH signifies the vibrational momentum of the H-H bond and p_HF signifies the translational momentum of F towards H₂. For the reactions ran, only 2, 6and 8 were reactive and the p_HH of reaction 2 and 6 have a higher absolute value than reaction 8, showing that more vibrational energy is put in than translational.

The total energy of reaction 2 and 6 is higher than reaction 8, indicating that reaction 2 and 6 are not as efficient as reaction 8. This can be explained by the exothermic nature of the reaction, which according to Polanyi's rule, is better promoted by translational energy. Since more vibrational energy was present in reaction 2 and 6, the reaction was less efficient.

HF + H

For this reaction, the initial condition of r_HF = 91 pm and r_HH = 220 pm is used, with both p_HF and p_HH being varied According to Polanyi's rules the reverse of the above would be true, since this reaction is endothermic. Therefore, it is expected that high vibrational momentum and low translational momentum would produce the most efficient reaction (I.e. lower total energy).

Reaction No.	pHH/ g.mol-1.pm.fs-1	pHF/ g.mol-1.pm.fs-1	Etot	Reactive?
1	-22	-0.1	-77.798	Yes
2	-10	-10	-556.972	No
3	-0.1	-26	-206.404	Yes

Reaction 1 was given with high vibrational energy and low translational energy. Although reactive, the total energy was relatively high, showing an inefficient reaction. When the conditions are reversed in reaction 3, the total energy lowers by almost three-fold, showing a large increase in efficiency. Reaction 2 was given the same vibrational and translational momentum and resulted in an unsuccessful reaction. All the above observations support the Polanyi's empirical rule for endothermic reactions.

Good systematic analysis! Well done!