MRD:RS7913
The Transition State
At a minimum and at a transition state, the total gradient of the potential energy surface is zero, i.e. ∂V(ri)/∂ri=0. The transition structure is a saddle point in the potential energy surface, however a minimum is simply a minimum in the surface. In other words, the transition state is a maximum on the minimum energy path from reactants to products.
(Fine up to here. Je714 (talk) 11:04, 15 May 2017 (BST))
One can therefore distinguish minima and transition structures by starting trajectories near the transition state or saddle point with no initial momentum and inspecting in which direction the geometry will ‘roll’. It will roll away from a transition state geometry, however it will roll towards a minimum and, if it reaches that minimum with sufficiently low momentum, settle at that mimimum.
(Although technically not wrong, this is an ad hoc description. We're looking for a general definition here. You should be discussing the difference in curvatures between a minimum, a maximum and a saddle point in a two-dimensional surface. You can express that with words (which you did up to a point in your above explanation) or use the mathematical definition of curvature (partial second derivatives). Check this for more details (https://www.wikiwand.com/en/Second_partial_derivative_test) Je714 (talk) 11:04, 15 May 2017 (BST))
H + H2 System
Trajectories from r1 = r2: locating the transition state

The transition state position, rts, was estimated to be 0.9077 A, and is defined as a saddle point in the potential energy surface. At this position, both internuclear distances - AB and BC - remain constant, as can be seen in Figure 1. Since no initial momentum has been supplied to the system and the gradient of the potential energy surface is zero at this maximum, there is no force 'pushing' the geometry of the system to change. Therefore the atoms will not move, and the geometry of the system will remain at this point on the potential energy surface.
Trajectories from r1 = rts+0.01, r2 = rts

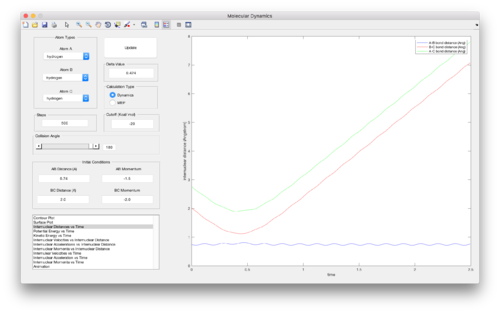
As can be seen from the surface plots of these two trajectories calculated, the mep trajectory (left) follows the valley floor directly as the molecule ‘B-C’ is formed while A moves away. Since this minimum energy path calculation corresponds to infinitely slow motion – at each time step the velocity is reset to zero – none of the potential energy of the system is converted into kinetic energy in the molecule ‘B-C’ as it is formed, meaning the molecule has no vibrational energy. The potential energy of the system is essentially kept constant. However, in the dynamics trajectory (right), molecular vibrations can be seen in the molecule ‘B-C’ that is formed. Since some of the potential energy in a system will be converted into vibrational energy as a diatomic is formed, the dynamics trajectory provides a more realistic account of the motion of the atoms during the reaction.
(Thorough explanation. GJ. Je714 (talk) 11:05, 15 May 2017 (BST))
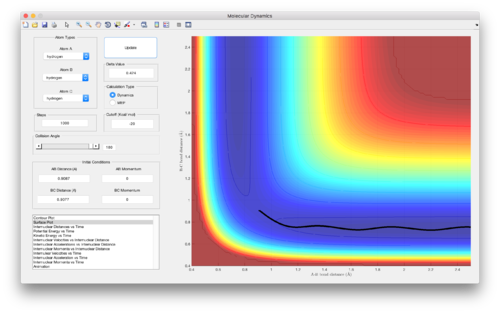
Reactive and unreactive trajectories from initial positions r1 = 0.74 and r2 = 2.0
| Figure | p1 | p2 | Reactivity |
|---|---|---|---|
| 4 | -1.25 | -2.5 | Reactive |
| 5 (and 6) | -1.5 | -2.0 | Unreactive |
| 7 | -1.5 | -2.5 | Reactive |
| 8 | -2.5 | -5.0 | Unreactive |
| 9 | -2.5 | -5.2 | Reactive |
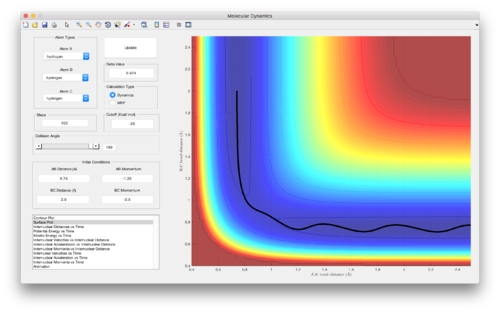

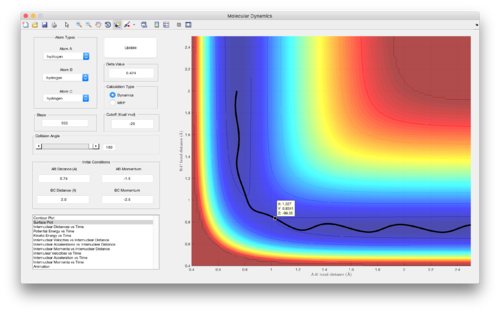
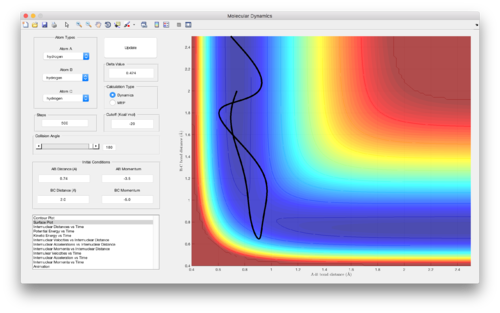
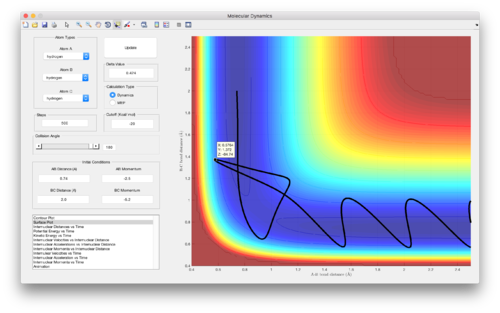
(Good discussion. Je714 (talk) 11:06, 15 May 2017 (BST))
Transition State Theory
Transition state theory assumes[1]:
1. The reactants and transition state complexes are in a special type of chemical equilibrium, known as quasi-equilibrium. For example, for a bimolecular elementary reaction between A and B which collide to form an activated complex, [AB]‡:
A + B <--> [AB]‡ --> P
all species in the system, including [AB]‡, will reach equilibrium. Even when the reactants and products are not in equilibrium with one another, the reactants are in equilibrium with the activated complexes that were reactant molecules in the immediate past. This is known as a quasi-equilibrium. Furthermore, each intermediate is sufficiently long-lived to reach a Boltzmann distribution of energies before converting into product(s) or reverting back to reactants.
(This is a statistical consideration of TST, and doesn't really apply here. After all, we're just looking at the collision between three atoms in isolation, not an ensemble of them. Je714 (talk) 11:10, 15 May 2017 (BST))
2. Collisions between molecules are completely elastic, and atomic nuclei behave according to classical mechanics.
3. Unless atoms or molecules collide with enough kinetic energy to form the transition structure, then the reaction doesn’t occur – this is contrary to theory of quantum mechanical tunnelling.
4. The reaction system (geometry) will pass over the lowest energy saddle point on the PES.
Assumption 1. is likely to be correct for the H + H2 system, since the transition state of the H + H2 system investigated are most likely sufficiently long-lived to reach a Boltzmann distribution of energies, since it is a simple arrangement of three protons and three electrons.
Assumption 2. is likely to be accurate for the H + H2 system, since hydrogen molecules in the gas phase do behave like charged masses when in adequately low concentration.
Assumption 3. may result in lower reaction rates predicted by transition state theory compared with experimental values, especially at low temperatures. Since quantum mechanical tunnelling may take place, some extra reactant molecules may be converted into product molecules, that transition state theory will not take account of.
Assumption 4. is likely to result in higher reaction rates predicted by transition state theory compared to reality, especially when the system has a lot of (kinetic) energy, since the geometry of the system may not always pass over the lowest energy saddle point on the PES when reactants are converting into products. This can be seen in Figure 9 above, where an alternative route has been taken on going from reactants to products, avoiding the formal transition state for the reaction. Furthermore, this assumption does not take into account barrier recrossing that could occur, as can be seen in Figure 8, which would once again lead to higher reaction rates predicted compared to reality.
(Correct. The biggest take home message here, which actually relates to what you see in the calculations, is barrier recrossing. Although not wrong, the other considerations are not relevant to this exercise. Je714 (talk) 11:10, 15 May 2017 (BST))
F-H-H System
The F + H2 reaction is highly exothermic, as can be seen by following the potential energy surface from the left to the right of Figure 10/11. This is due to the formation of the strong H-F bond formed, which releases a lot of energy, considerably more than that needed to break the weaker H-H bond. From the potential energy surface shown in Figure 10 and 11 (z-values on points indicated), the enthalpy of the reaction can be estimated to be ΔH= -133.8 – (-103.9) = 29.9 kcal mol-1 = 125 kJ mol-1. This agrees well an enthalpy of reaction calculated from empirically obtained average bond energies[2]: ΔH= H-F – H-H = 565 – 432 = 133 kJ mol-1.
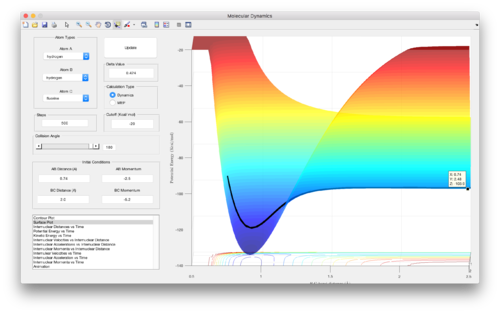

On the contrary, for the same reason, the H + H-F reaction is of course endothermic (from left to right of Figure 10/11), since it is the reverse of the F + H-H reaction. Energy is put into the system to break the strong H-F bond, which is not compensated for by the energy released on formation of the weaker H-H bond. The enthalpy of the H + H-F reaction is of the same magnitude but opposite sign of that for the F + H-H reaction. Once again, from the potential energy surfaces calculated, ΔH can be estimated to be -125 kJ mol-1.
The approximate position of the transition state of the F + H-H/ H + H-F reaction is shown in Figure 12, and is at an energy of -103.7 kcal mol-1. The Hammond postulate was employed to guide the search for this position, recognising that in the case of the exothermic H + H-F reaction, an early transition state will be observed close to the reactants, since the transition state – being the maximum in the minimum energy path from reactants to products – resembles the structure that it is closest to in energy. The opposite is true for the reverse endothermic H + H-F reaction, and the transition state is at the same point on the potential energy surface, as shown in Figure 12.

Therefore, the activation energies of these two reactions can be calculated as follows, by subtracting the energy of the reactants from the energy of the transition state:
Ea = ETS – Ereactants
F + H-H: Ea = -103.7 – (-103.9) = 0.2 kcal mol-1 = 0.84 kJ mol-1
H + H-F: Ea = -103.7 – (-133.8) = 30.1 kcal mol-1 = 126 kJ mol-1
(Could've run a sufficiently long MEP calculation starting from the TS geometry to get more accurate values for this. Je714 (talk) 11:12, 15 May 2017 (BST))
Reaction Dynamics
As with any chemical reaction, the law of conservation of energy is obeyed. In the dynamics calculation, energy can only switch between potential and kinetic energy. As can be seen in Figure 13, and also the “Animation” for the reactive trajectory, the potential energy released during the F + H-H --> H-F + H reaction is released as vibrational energy in the H-F molecule formed. Oscillations of greater amplitude can be seen in the products (horizontal line in Figure 13) compared to the reactants (vertical line in Figure 13).

However, this conversion of potential energy into vibrational energy can be most clearly seen in a plot of “Internuclear Momentum vs Time” (Figure 14). Large oscillations in the red line corresponding to B-C internuclear momentum represents vibrational oscillations in the B-C, i.e. H-F, molecule formed.
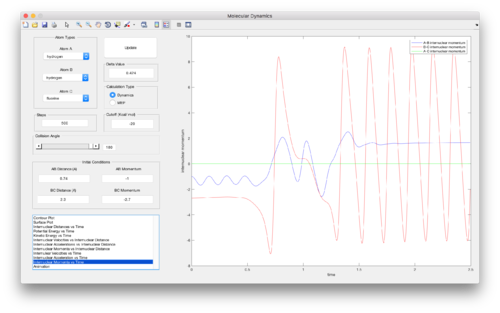
This vibrational energy released could be confirmed by using IR spectroscopy to detect the polar H-F bond formed. The non-polar H-H bond in the reactant molecule would not be visible in an IR spectrum. Furthermore, the energy released could be measured using calorimetry. Since each vibrational degree of freedom contributes approximately (1/2)kbT of energy at thermal equilibrium (equipartition theorem), the vibrational energy released as the reaction takes place can be measured by the temperature change of the system.
Polanyi's Empirical Rules
Polanyi derived empirically that reactions with an early transition state, such as F + H-H --> F-H + H, are most efficient for higher translational energies of the reactant molecules colliding. This can be seen in Figures 15 and 16, where an increase in kinetic energy of H-H results in a results in the reaction taking place, when the overall energy of the system, as well as starting positions of the molecules, is kept constant.[3]
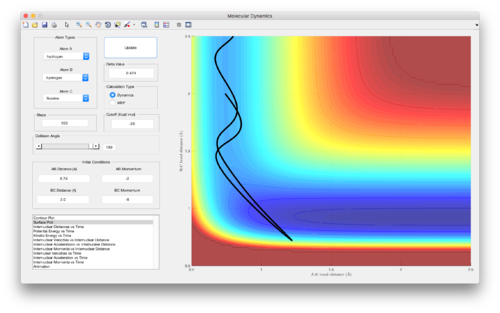
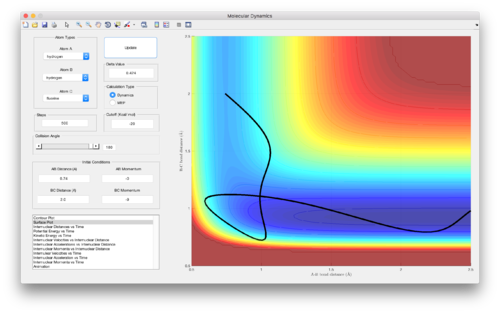
Polanyi also derived that reactions with a late transition state, such as H + H-F --> H-H + F, are most efficient when there is higher vibrational energy in the reactant(s). A similar analysis carried out on the H + H-F --> H-H reaction, keeping all variables constant apart from the distribution of energy into kinetic and vibrational energy, as done in Figures 15 and 16, resulted in more efficient reactive trajectories when more energy was in the vibrations (vibrational energy) of H-F compared to the translational energy of the H and H-F particles colliding.
- ↑ Anslyn, Eric V.; Doughtery, Dennis A., Transition State Theory and Related Topics. In Modern Physical Organic Chemistry University Science Books: 2006; pp 365–373
- ↑ "Bond Energies", https://chem.libretexts.org/Core/Physical_and_Theoretical_Chemistry/Chemical_Bonding/General_Principles_of_Chemical_Bonding/Bond_Energies, Accessed May 2017.
- ↑ P. Atkins, J. De Paula, Atkin's Physical Chemistry, 10th Edition, 2014, OUP.
