MRD:R1chie

EXERCISE 1: H + H₂ system

Q1: On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?

Answer: The transition state of a reaction can be defined as the saddle point on the potential energy surface and it is the maximum of the lowest energy pathway. At the saddle point, the gradient of the energy function is to be zero. Mathematically, assume the potential energy is a function of positions r₁ and r₂ which are the distance of atom A and B and that of atom B and C respectively, the function can be represented as V(r₁,r₂).

Let 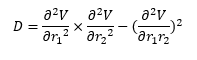, if D < 0, then potential energy is at its saddle point.

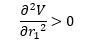
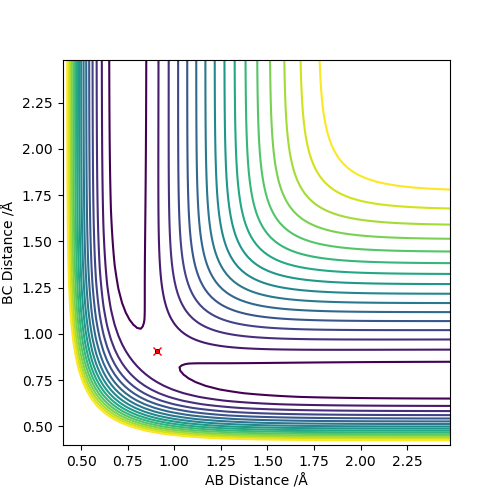
If D > 0 and , then potential energy is at its local minimum.

Q2: Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

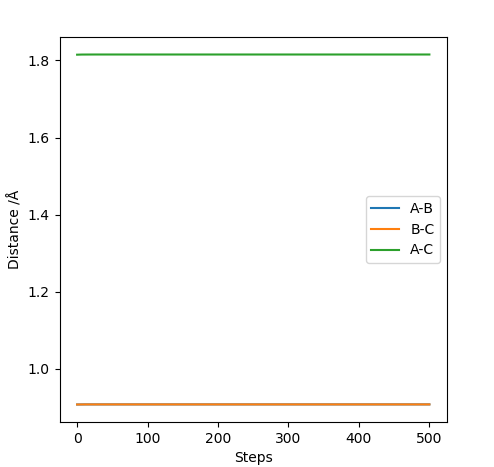
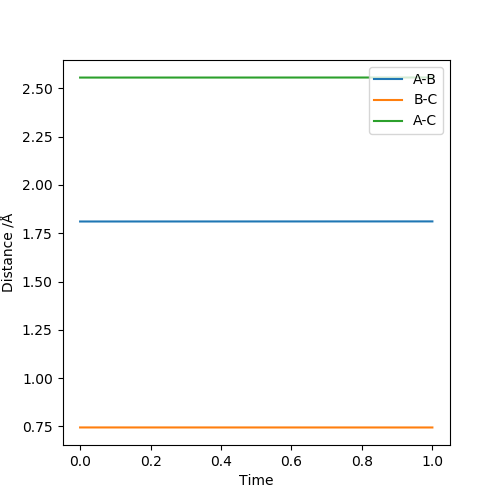
Answer: The estimated r_ts value is to be 0.9075 Å. When r₁=r₂=0.9075 Å and p₁=p₂=0, the system reaches its transition state because the internuclear distance does not change with varying time. Good illustrations. Pu12 (talk) 19:44, 6 June 2019 (BST)

Figure 1: The Contour Graph of the Minimum Potential Energy

Figure 2: Internuclear Distance v.s. Time

Q3: Comment on how the mep and the trajectory you just calculated differ.

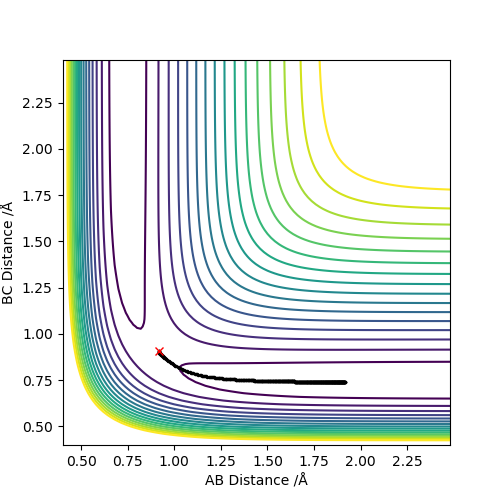
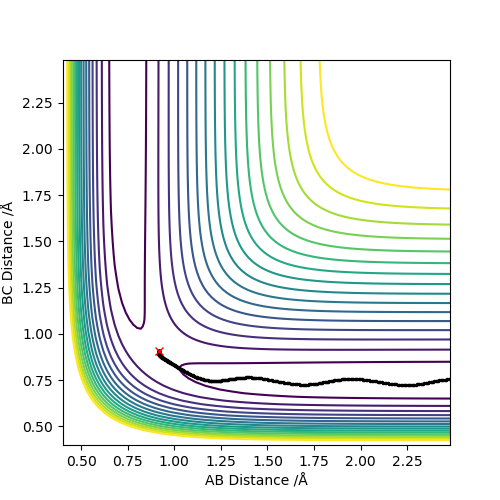
When MEP method is applied, the momenta and velocities are always set to be zero. That suggests during the reaction, the kinetic energy is also to be zero and there is no vibration of molecules hence no oscillation illustrated in Figure 3. However, when dynamic method is applied, the kinetic energy is not to be zero and oscillation of molecules is present in the contour graph, Figure 4.

Q4: Complete the table below by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?

p₁	p₂	E_tot	Reactive?	Description of the dynamics	Illustration of the trajectory
-1.25	-2.5	-99.018	YES	Atom C approaches molecule AB with sufficient momenta and kinetic energy to overcome the activation barrier. The reaction occurs successfully.	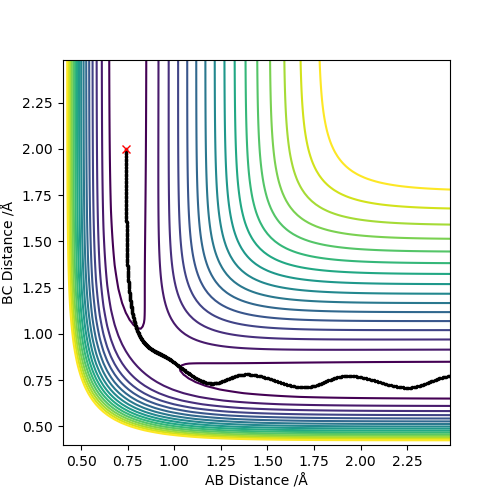Figure 5: MEP Method Contour Graph with p₁ = -1.25 and p₂ = -2.5
-1.5	-2.0	-100.456	NO	Atom C approaches molecule AB with insufficient momenta and kinetic energy to overcome the activation barrier. The reaction does not happen.	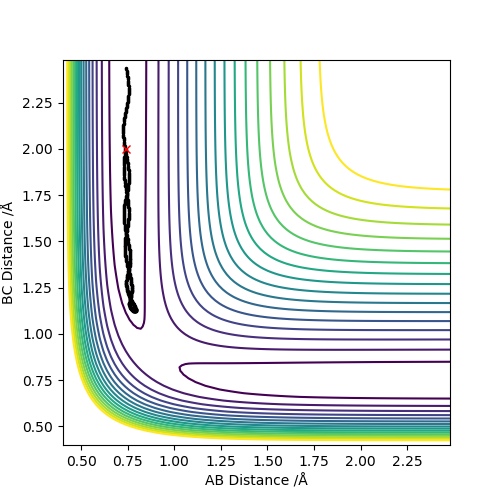Figure 6: MEP Method Contour Graph with p₁ = -1.5 and p₂ = -2.0
-1.5	-2.5	-98.956	YES	Atom C approaches molecule AB with sufficient momenta and kinetic energy to overcome the activation barrier. The reaction occurs successfully.	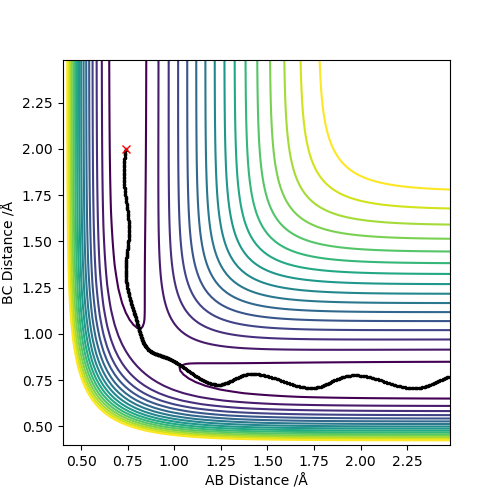Figure 7: MEP Method Contour Graph with p₁ = -1.5 and p₂ = -2.5
-2.5	-5.0	-84.956	NO	Atom C approaches molecule AB with sufficient momenta and kinetic energy to overcome the activation barrier and the trajectory passes through the transition state region. The reaction occurs successfully but the product is reverted into vibrating reactants at the end.	Figure 8: MEP Method Contour Graph with p₁ = -2.5 and p₂ = -5.0
-2.5	-5.2	-83.416	YES	Atom C approaches molecule AB with sufficient momenta and kinetic energy to overcome the activation barrier and the trajectory passes through the transition state region. The product is formed and reaction occurs successfully.Should mention that recrossing occurs. Pu12 (talk) 19:44, 6 June 2019 (BST)	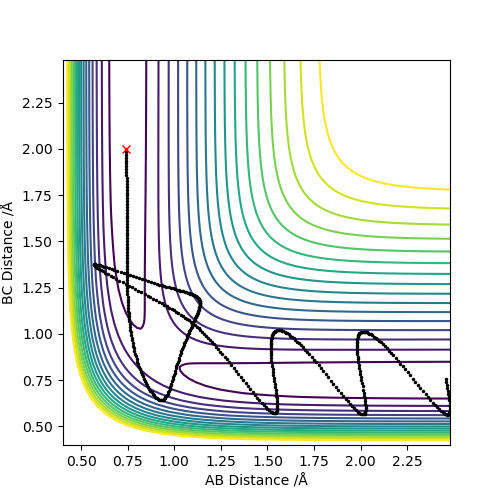Figure 9: MEP Method Contour Graph with p₁ = -2.5 and p₂ = -5.2

Decent explanations, but should discuss vibrations in each case. Pu12 (talk) 19:44, 6 June 2019 (BST)

Conclusion:

1. For all successful reactions, the reactants have sufficient initial momenta and kinetic energy.

2. For all unsuccessful reactions, increasing initial momenta can be possible to result in successful reactions.

3. However, sufficient momenta can not guarantee the successful reactions because the products are probably reverted into reactants.

Q5: State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

Answer: Transition State Theory ¹:

1. The Born-Oppenheimer Approximation: the electronic and nuclear motion are separated rested on the significant mass difference.

2. In the transition state, motion along the reaction coordinate may be separated from the other motion and treated classically as translation.

3. Molecules that have crossed the transition state cannot reform reactants.

4. The reactant molecules follow the Maxwell-Boltzmann distribution.

5. Even in the absence of equilibrium between the reactant and the product, the transition states that are becoming the product follows the Maxwell-Boltzmann laws.

From the experimental results, products can be reverted into reactants even though the reaction occur successfully. Rested on this effect, the rate of reaction is possibly decreased.

Exercise 2:F - H - H system

Q6: By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved? Locate the approximate position of the transition state.

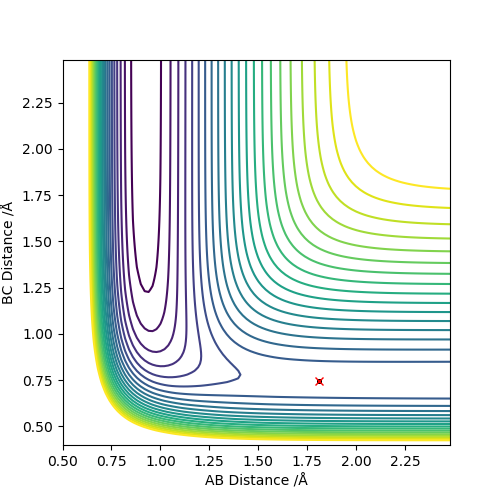
Figure 2: The Internuclear Distance v.s. Time Plpt of F+H2 at r₁ = 1.811 Å and r₂ = 0.745 Å

E(F-H) = -565 KJ/mol

E(H-H) = -436 KJ/mol

The figures above illustrate the reaction F + H2 → H-F + H. In this reaction, the H-H bond is broken and H-F bond is formed. Since the bond energy of H-H is lower than that of F-H and therefore, the reaction is exothermic and the enthalpy change is -129 KJ/mol. You are correct about which reaction is exothermic or endothermic, but the question asks you to figure this out from the potential energy surfaces not just bond energies. If you have a look on the surface plots you can see that the reactants are either higher or lower in energy for each of the reactions, indicating how the enthalpy change goes. Pu12 (talk) 19:44, 6 June 2019 (BST)

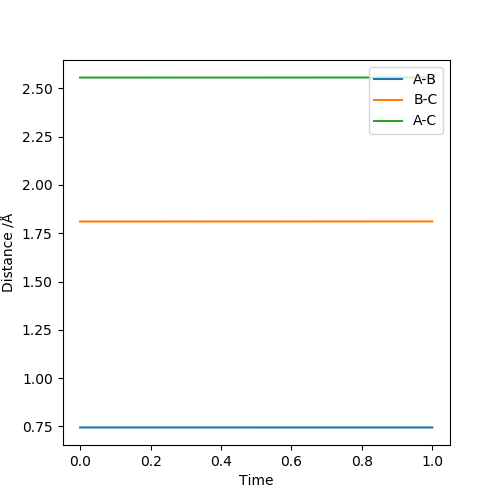
The estimated transition state positions are r₁ = 1.811 Å and r₂ = 0.745 Å. At these positions, the internuclear distance do not change with varying time.

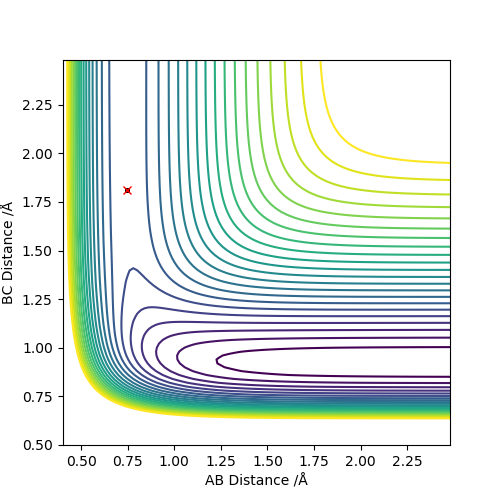
Figure 4: The Internuclear Distance v.s. Time Plot of F+H2 at r₁ = 0.745 Å and r₂ = 1.811 Å

The figures above illustrate the reaction H-F + H → H2 + F. In this reaction, H-F bond is broken and H2 is formed. Since the bond energy of H-H is lower than that of F-H and therefore, the reaction is endothermic and the enthalpy change is +129 KJ/mol.

The estimated transition state positions are r₁ = 0.745 Å and r₂ = 1.811 Å. At these positions, the internuclear distance do not change with varying time.

Q7: Report the activation energy for both reactions.

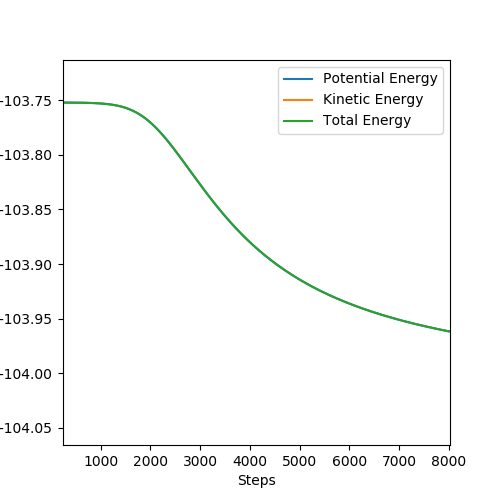
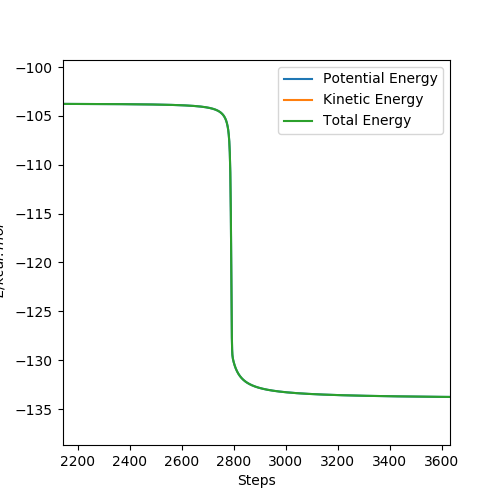
Figure 5: The Plot of Activation Energy of F+H2

Figure 6: The Plot of Activation Energy of H-F + H‎

It would help to show how you got the activation energy from these graphs. Pu12 (talk) 19:44, 6 June 2019 (BST)

Both reactions have the same transition state. These are two directions of the same reversible reaction.

For F + H₂ → HF + H, the activation energy is small as 0.209 kcal/mol because the reaction is exothermic and reactants are close to transition state.

For H + HF → H₂ + F, the activation energy is large as 29.887 kcal/mol because the reaction is endothermic and reactants keep away from the transition state.

Q8: In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.

A: The initial condition is set to be r_AB = 1.811, r_BC = 0.745, p_AB = -0.8 and p_BC = -0.5. During the reaction, it can be observed there is a decrease in potential energy and an increase in kinetic energy. The kinetic translation energy being raised can be confirmed by measuring the temperature of the reacting mixture. And there is also a rise in the vibrational kinetic energy and shown on the momenta v.s. time graph, it can be noticed that the oscillation of H-F product is stronger than that of H-H reactant which can be measured by IR spectrum. You don't have to talk about temperature and vibrational energy separately as the vibrations are basically what temperature measures. Pu12 (talk) 19:44, 6 June 2019 (BST)

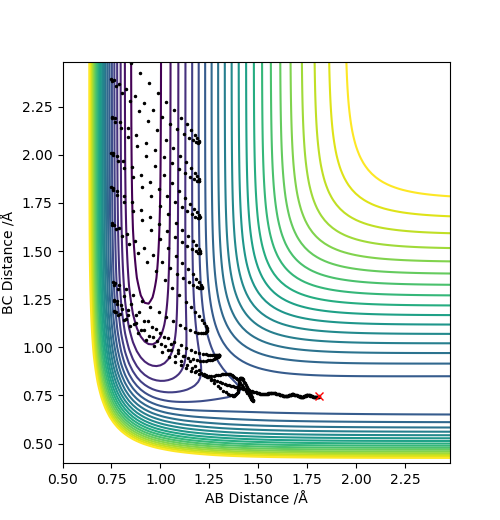
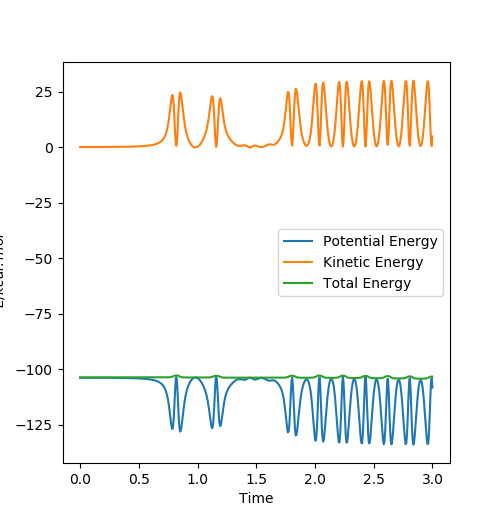
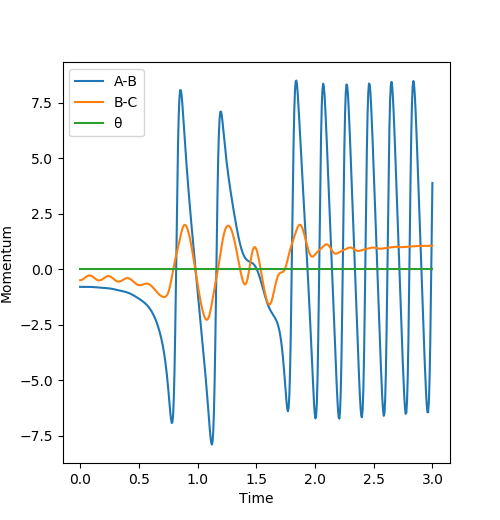
Q9: Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Figure 10: The Contour Plot of H-F + H Reaction: High Vibrational and Low Translational Energy

Figure 11: The Contour Plot of H-F + H Reaction: Low Vibrational and High Translational Energy

Figure 12: The Contour Plot of F+H2 Reaction: High Vibrational and Low Translational Energy

Figure 13: The Contour Plot of F+H2 Reaction: Low Vibrational and High Translational Energy

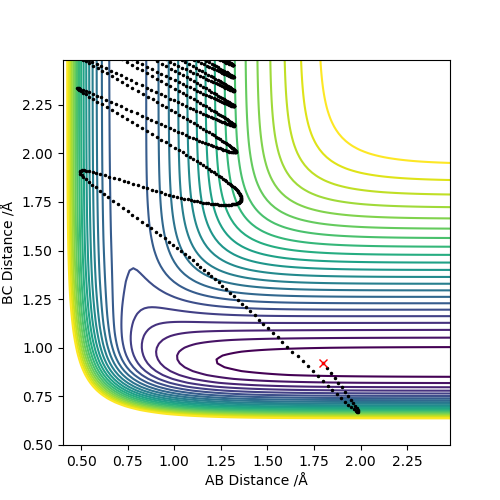
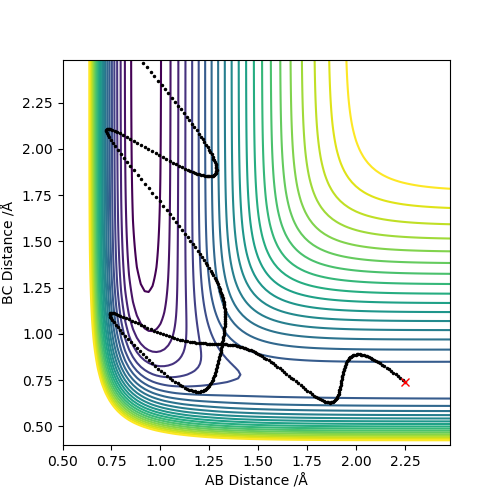
For exothermic reaction, F + H2 → H-F + H, it has an early transition state. The translational kinetic energy is more effective than vibtational energy to overcome the barrier.

For endothermic reaction, H-F + H → F + H2, it has a late transition state. The vibrational kinetic energy is significantly more effective than translational energy.

According to what?Pu12 (talk) 19:44, 6 June 2019 (BST)

This is a good report and you don't make any big mistakes, but you should include more discussion in your answers as it is hard to judge your level of understanding through answers that are just direct statements. Pu12 (talk) 19:44, 6 June 2019 (BST)

Reference

1. J. I. Steinfeld, J. S. Francisco, W. L. Hase, Chemical Kinetic and Dynamics, Prentice-Hall, New Jersey, 1998

EXERCISE 1: H + H2 system