MRD:PS4615

Molecular Reaction Dynamics

H + H₂ system

Dynamics from the transition state region

The following illustrates the trajectory of the reaction at different reaction coordinates.

Figure 1:The whole reaction trajectory.

Figure 2:The position of the transition state indicated by the arrow.

Q1. What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

At the minimum and at the transition state in the potential energy surface, the total gradient has a value of zero, as both of the points are at the turning points of the PES $(\frac{dV}{d{r}_i}=0)$. The minimum and the transition state can be distinguished as the transition state is the saddle point of the plot. As a result, the minimum point has to satisfy the following criterion:

$\frac{\partial V^2(r_i)}{\partial r_i^2}>0$

This is so in all of the directions in the reaction coordinate.

Whereas for the transition state, the second derivative of the PES $(\frac{\partial V^2(r_i)}{\partial r_i^2})$ has a different sign at different directions in the reaction coordinate (in this case it is in the r_ab and r_bc).

(Fv611 (talk) 14:47, 9 June 2017 (BST) Overall good, but the term is "stationary points", not "turning points".)

Trajectories from r₁ = r₂: locating the transition state

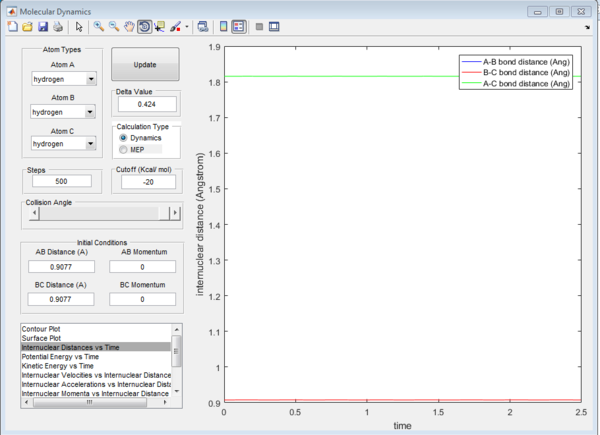
Q2. Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.

The transition state position (rts) is when the internuclear distance between the hydrogens are the same. This can be initially estimated from the PES as shown in figure 1. From there, a better approximation of the transition state position can be obtained by a trial solution method using the Internuclear distance - time plot. When the hydrogen atoms are placed at exactly this position with zero momenta, it will stay here with respect to time. This can be explained as follows. At the transition state, the change in the potential energy of the system is zero $(\frac{dV}{d{r}_i}=0)$, hence the resultant force on the hydrogens is zero. Therefore, the displacements of the hydrogens at this position (with zero momenta) would be constant. Hence as the displacements is the same over time, the vibrational energy of the system is zero. For this system, the transition state position is at the internuclear distance of roughly 0.9077 Å, as this can seen that the distance is constant over time (see figure 2).

Figure 3: No trajectory is observed as the system is at the transition state.

Figure 4: The internuclear distance vs Time plot showing that the distance is constant.

Calculating reaction path

The following are the Internuclear Distances vs Time graph and Internuclear Momenta vs Time graph for the trajectory from r₁ = r_ts+δ, r₂ = r_ts.
.

Figure 5: The Internuclear Distances vs Time graph and Internuclear Momenta vs Time.

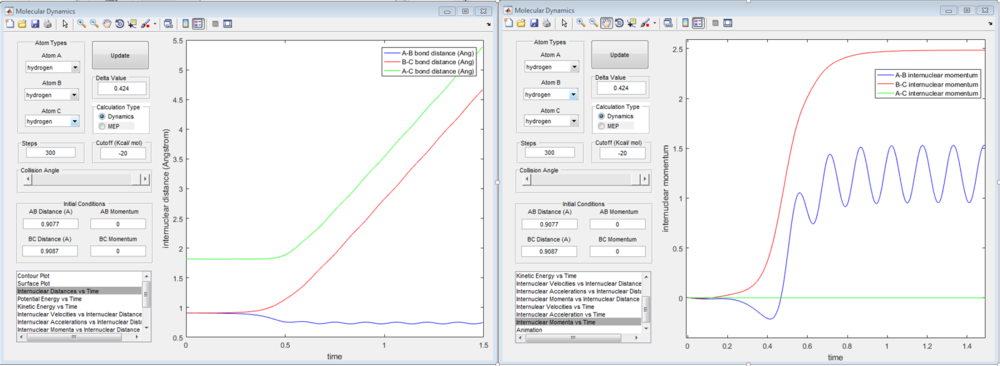
From the calculations it was determined that the final values of the positions r_BC and r_AB are 6.00Å and 5.28Å respectively. In addition, at large value of time, the average values of momenta of B-C, A-B and A-C are 2.48, 1.22 and 0.00 respectively.

Minimum Energy Path (MEP) vs Reaction Dynamics - Trajectories from r₁ = r_ts+δ, r₂ = r_ts

Q3. Comment on how the mep and the trajectory you just calculated differ.

In the MEP tracjectory, it can be seen that the trajectory had only travelled a small distance from the transition state (using 500 steps for both method). In addition, molecular vibration is observed for the MEP trajectory compared to the dynamics trajectory. This is due to the fact that the energy of the system is mainly translational. In each and every time step, the velocity is allowed to increase and then set to zero in the next step. As a result, the reactants loses their momenta and resulted in the small trajectory observed. This means that for the MEP, the inertia of the trajectory is not taken into account.

For the dynamic method, inertia is taken into account, and the trajectory extends all the way to the products. In addition, molecular vibration is observed throughout the trajectory (see figure 5). As inertia is taken into account, the velocity of the trajectory does not go to zero and the path is longer.

Figure 6: Comparison of the MEP trajectory and the dynamic trajectory.

Figure 7: The results obtained from using the MEP method with 20000 steps.(A)The trajectory of the MEP on the potential energy surface.(B)The kinetic energy of the system vs time for the MEP.(C)The potential energy vs time of the MEP..

Figure 8: The results obtained from using the Dynamics method.(A)The trajectory on the potential energy surface.(B)The kinetic energy of the system vs time.(C)The potential energy vs time graph of the system.

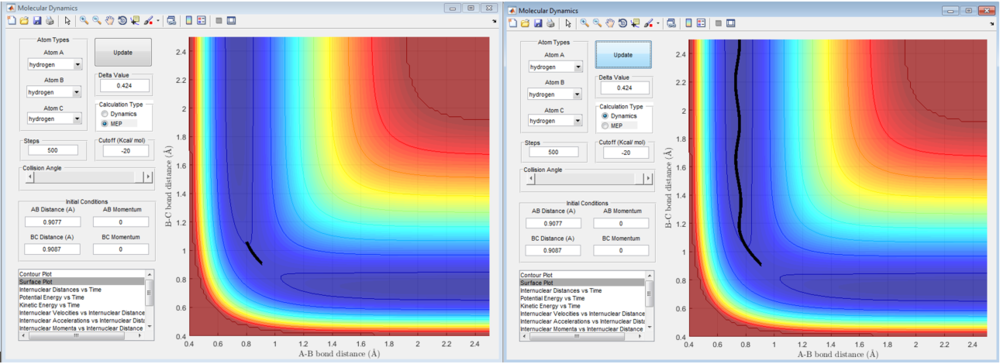
Different reaction trajectories and its reactivity

Q4. Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.

p1	p2	Reactivity
-1.25	-2.5	Reactive
-1.5	-2.0	Unreactive
-1.5	-2.5	Reactive
-2.5	-5.0	Unreactive
-2.5	-5.2	Reactive

Figure 9: This trajectory is reactive. As can be seen, the trajectory passes through and moves pass the transition state forming the product. This is because the reactants have enough kinetic energy to overcome the energy barrier and form the products. In addition, it can be seen that hydrogen A approaches hydrogen B and C with purely translational energy, where it is then converted to vibrational energy afterwards as seen above. The reaction also is driven to completion.

Figure 10: This trajectory is not reactive. The combined momentum of the reactants is not enough to overcome the energy barrier, resulting in the transition state not being reached. The vibrations of the resulting system after the approach has greater vibrational energy as p₂ has a greater magnitude than p₁

Figure 11: This trajectory is reactive. This is because the combined momentum (in other words enough kinetic energy) of the reactants has enough energy to overcome the barrier and form the products. Also, the product has a greater vibrational energy as (compared to the first case above) because p₁ has a greater magnitude.

Figure 12: This trajectory is not reactive. The combined momentum is enough to overcome the energy barrier. Although, the reactants goes pass through the transition state but returns back and goes back to the reactants. Hence because of this, products are not formed. One explanation to this is that the vibrational energy of the products may be too high that the reaction reverses and goes back to the reactants. Hence, for this case, further investigation must be carried out to confirm the results.

Figure 12: This trajectory is reactive. The combined reactants has enough momentum to overcome the reaction barrier to reach the transition state. Although in this case, the transition state was reached many times, the product eventually formed .

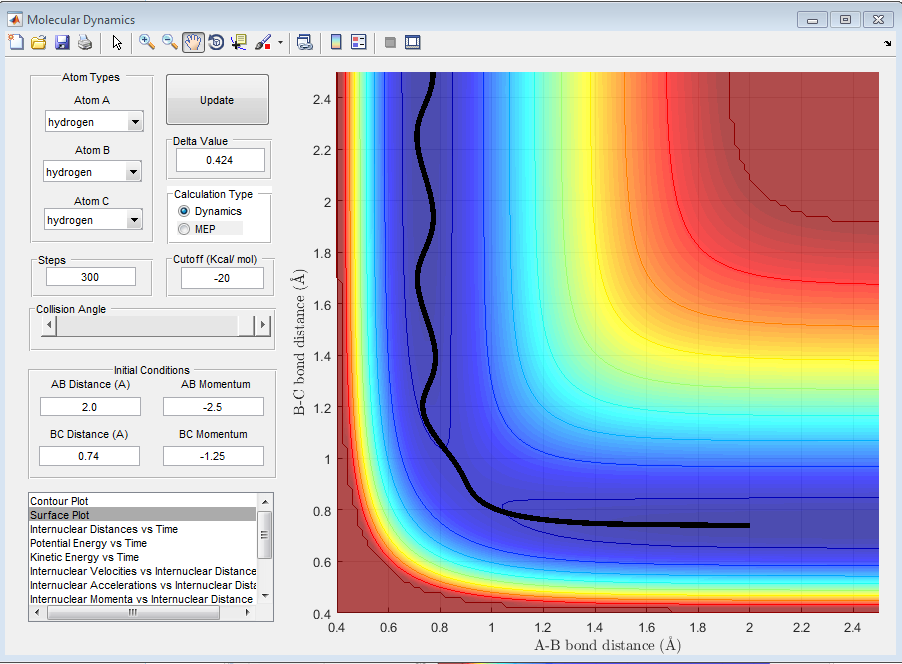
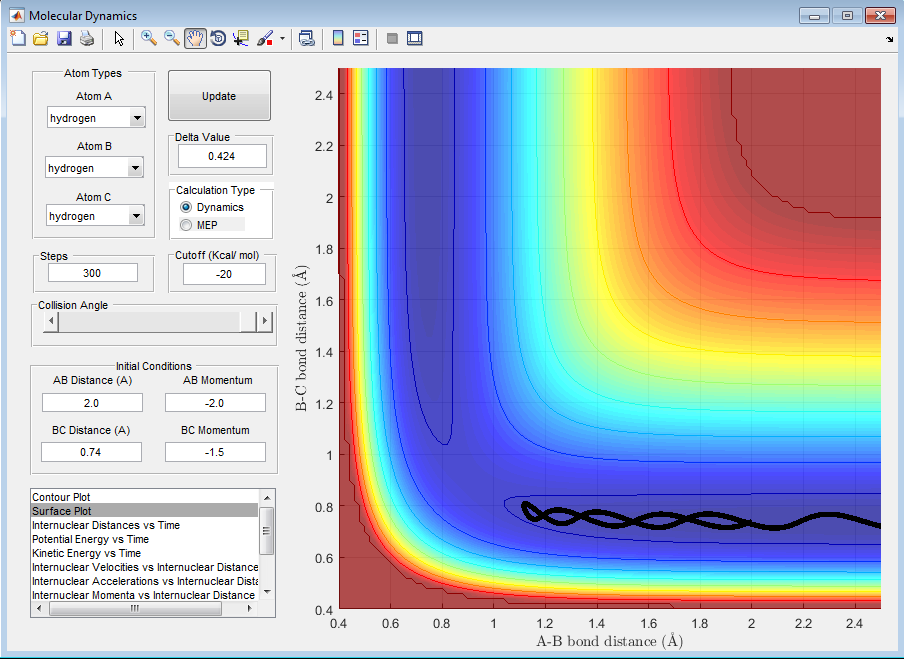
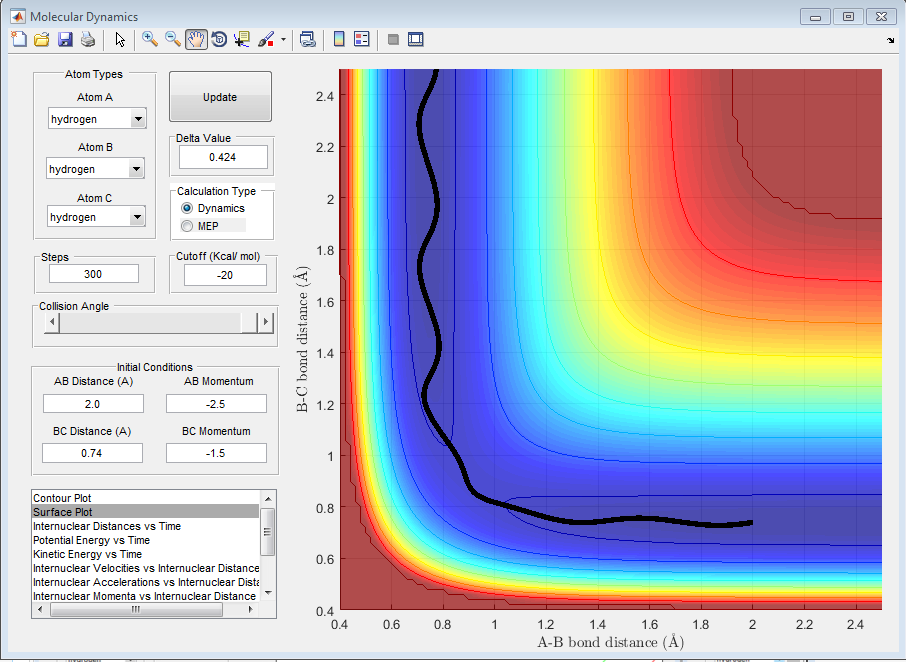
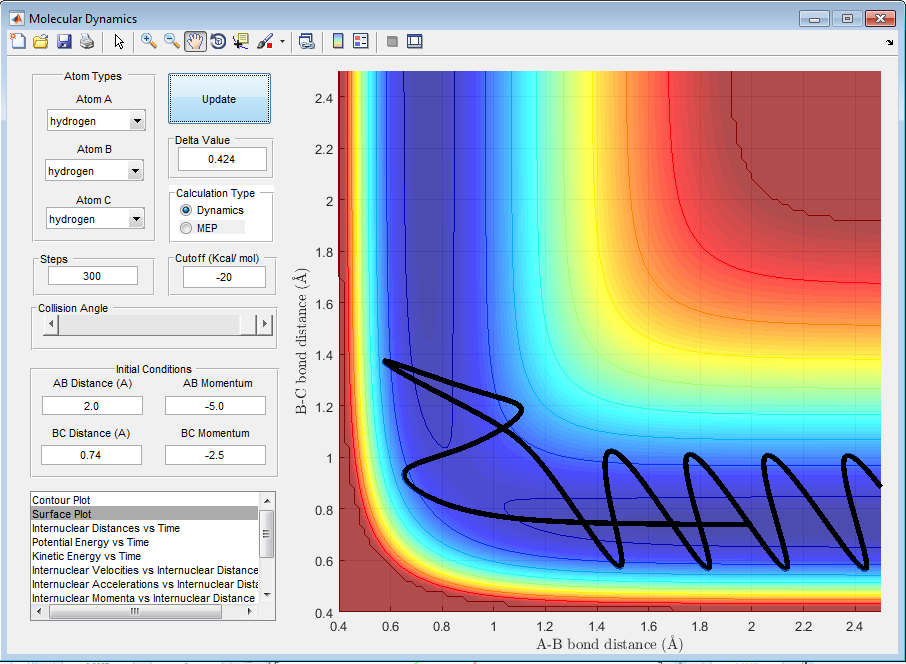
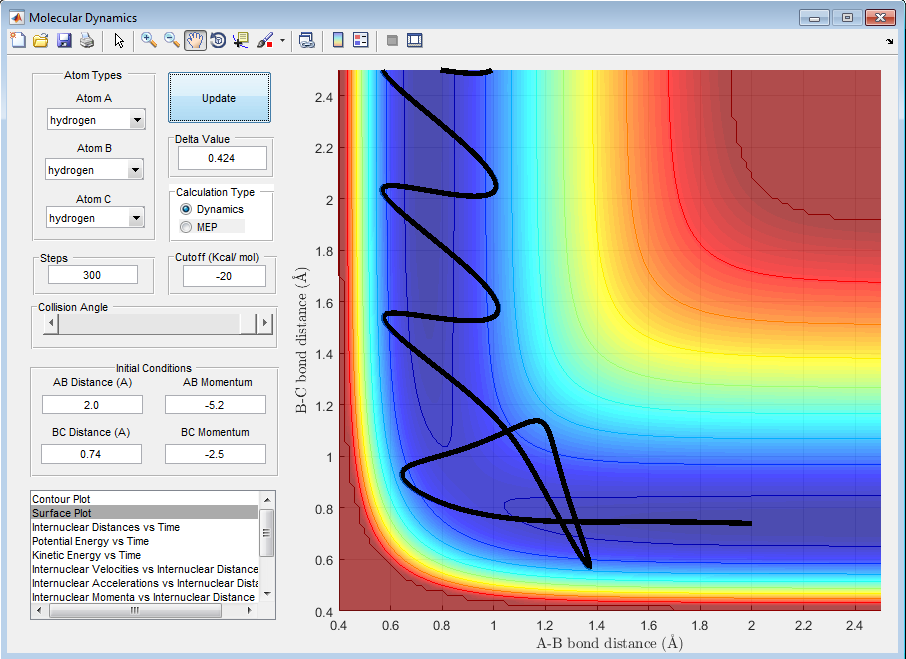
By observing the reactivity of the system at different initial conditions, it can be clearly deduced that the total energy of the reactants does not determine the completion of the reaction, as this also depends on the orientation and the type of energy. In addition, it can be deduced that the reaction of H + H₂ is an exothermic reaction, as the translational energy of the reactants drives the reaction to completion.

(Fv611 (talk) 14:47, 9 June 2017 (BST) Very good discussion)

Q5. State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

The following are the main assumptions of the Transition State Theory:

1. Once the transition state of the reaction is reached, products must form afterwards.

2. The transition state alone determines the kinetics (rates of reactions) of reactions.

3. A special type of chemical equalibrium, called quasi-equilibrium is reached between the transition state and the reactants.

4. Quantum tunnelling does not occur, and the motions of the reactants purely obey classical mechanics.

5. The molecules obey the Boltzmann distribution when they occupy different energies level (can be electronic, vibrational etc.).

The reaction rates can be predicted and compared with experimental values by using the first assumption mentioned above. From the section above, it can be seen that the first three conditions follows this assumption, but the last two does not, as the transition state was reached more than once. Also, the transition state was reached in the penultimate case, but the product was not formed.

(Fv611 (talk) 14:47, 9 June 2017 (BST) Very good discussion)

F - H - H system

PES inspection

Q6. Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

From the PES shown below, it can be deduced that the energy of the reactants is higher than the products, hence it is an exothermic reaction for the reaction of F + H₂. As for the reaction of H + HF, the energetics is simply reverse, which makes it an endothermic reaction.

Figure 14: PES of the F - H - H system. As can be seen, the reactants higher energy than the products (for F + H₂ reaction).

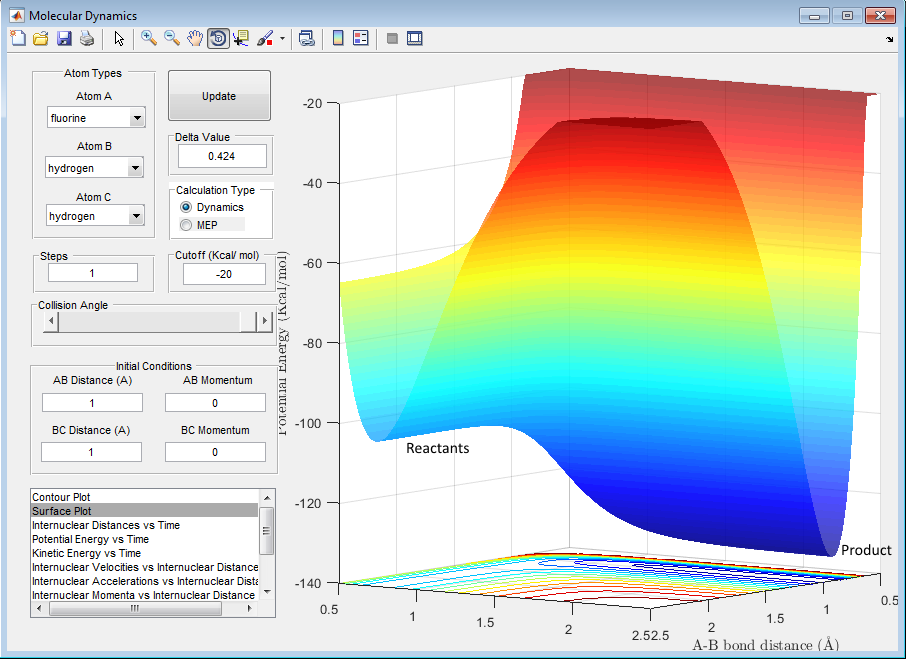
From the reaction of F + H₂, it can be deduced that as the product has a lower energy (HF), this indicates that the bond stregth of HF is greater than the bond strength of H₂. This is because essentially, the enthalpy change of the reaction is as follows:

ΔH = Energy required to break all the bonds - Energy released from bond formation

As the reaction is exothermic, the energy released from forming H-F bonds must be greater than the energy required to break the H-H bond. This means that the H-F bond is stronger than the H-H bond. This was confirmed from existing experimental data, where the energy required to break H-H is 436 kJ/mol whereas it is 570 kJ/mol for H-F.

Q7. Locate the approximate position of the transition state.

Again, the transition state of the reaction was determined by the trial solution method, where the Internuclear distance vs time plot indicates whether the trajectory is at the transition state or not. The transition state was found to be at a distance of 1.810 Å for the H-F internuclear distance and 0.745 Å for the H-H internuclear distance.

Figure 15: PES of the F - H - H system at the transition state.

Figure 16: The Internuclear Distance vs Time plot showing a straight line.

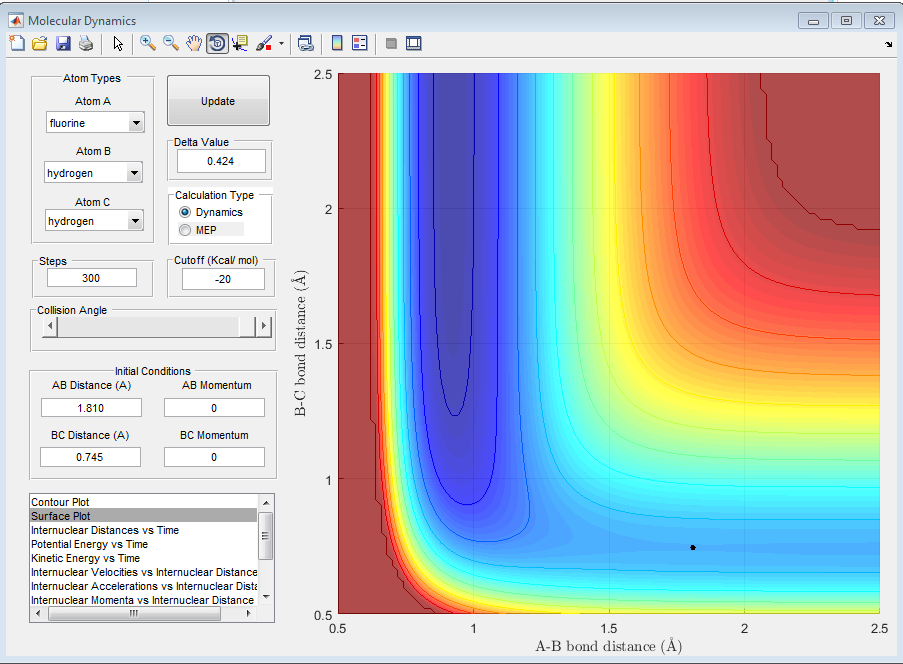
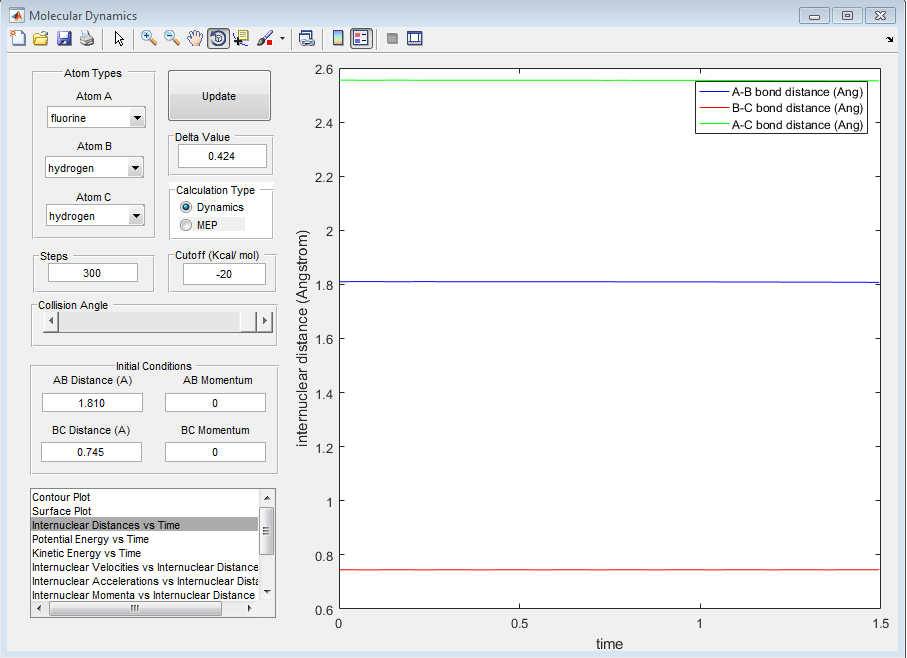
(Fv611 (talk) 14:47, 9 June 2017 (BST) Could have used Hammond's postulate to make educated guess about the location of the TS.) Q8. Report the activation energy for both reactions.

The activation of a reaction is determined by finding the difference between the energy of the reactants and the transition state. The following are the activation energies of the reaction.

For F + H₂: -103.3 - (-103.4) = +0.1 kcal/mol

For H + HF: -103.3 - (-133.4) = +30.1 kcal/mol

Figure 17: The MEP trajectory used to determine the activation energy.

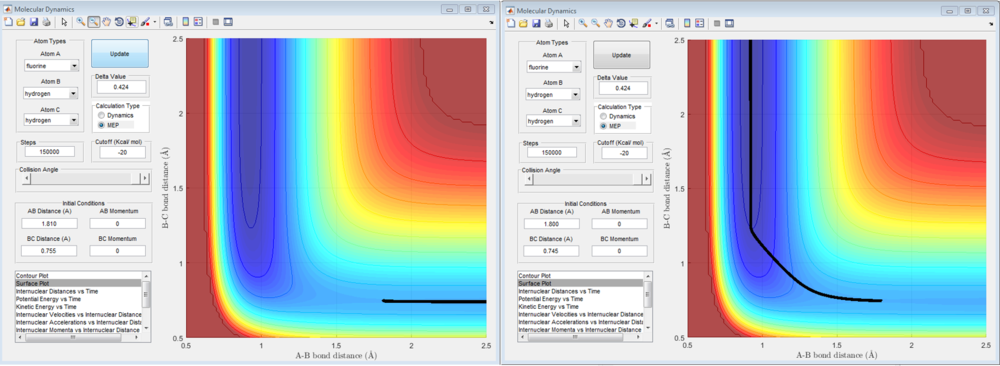
(Fv611 (talk) 14:47, 9 June 2017 (BST) No justification for your values. Should show your results or people have to trust you did the work, and most people won't.)

Reaction Dynamics

The following condition is an example where the reaction of F + H₂ proceeded to the product. It was found that not the orientation and the form of the energy of the system has a huge dependent on the success of the reaction trajectory. For this particular case, the transition state was crossed multiple times before the trajectory proceeded to the product. In addition, it was found in many cases that lowering the combined momentum of the particles resulted in reactive trajectory.

Figure 18: A condition that resulted in reactive trajectory.

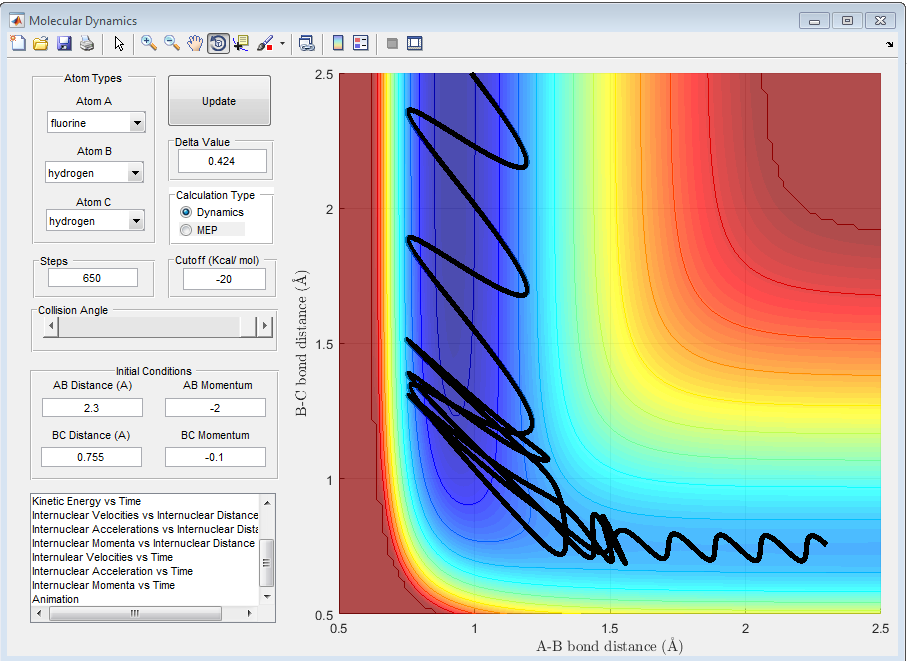
Q9. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

The law of conservation of energy states that energy cannot be created or destroyed. Energy can only change from one form to another. One of the ways in which a reaction system can release its energy through heat energy. In a reaction system, its energy can be simplified as having potential and kinetic energy. For an exothermic reaction, the excess energy of the system after the reaction can be lost as heat energy to the surrounding. Heat energy actually consist of both kinetic and potential energy. This lost of energy to the surrounding can be measured by a method called calorimetry. For a closed system, the energy lost by the reaction system (heat) to the surrounding can be measured by measuring the temperature of the whole system. This can heat energy gained by the surrounding can be calculated using basic thermodynamics.

In addition, the energy lost can also be measured spectroscopically. The energy lost by the system as vibrational energy can be in the form of photons, which can be detected by a spectrophotometer. The energy of the photon can be calculated through its frequency (E = hν).

(Fv611 (talk) 14:47, 9 June 2017 (BST) Showing a graph of the energy of the system would have helped you framing the discussion around the change in vibrational energy from reactants to products.) Q10. Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

The distribution of energy between different modes (mainly translational and vibrational) can affect reaction trajectories differently. According to Polanyi's Rule, it is stated that for a reaction with an early transition state, giving the reactants more translational energy (eg. increasing their momentum) would be more efficient in the reaction trajectory being reactive, overcoming the energy barrier. Although, it is not efficient to excite the reactants' vibrational energy. As for trajectories with late transition state, exciting the reactants vibrational energy is efficient and effective in overcoming the energy barrier, resulting in reactive trajectory. Conversely, translational energy, in this case, is not effective in overcoming the energy barrier, resulting in unreactive trajectories.

(Fv611 (talk) 14:47, 9 June 2017 (BST) Discussion is correct, but you should have provided examples.)