MRD:POLS
Transition state
The transition state of a reaction is a transient structure that exists at a saddle point on a potential energy surface. The gradient of the total energy equals zero and is the maximum of the minimum energy path of the potential energy surface. The minimum point of the surface also has a gradient of 0 and so in order to determine which critical point is a saddle or minimum point is to take the second derivative of the potential energy surface. If the second derivative is less than zero than it is a saddle point/transition state and if it is greater than zero it is a minimum.
∂2V(ri)/∂2ri> 0 'Minimum'
∂2V(ri)/∂2ri< 0 'Saddle point'
Locating The Transition state
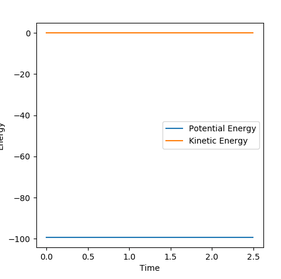
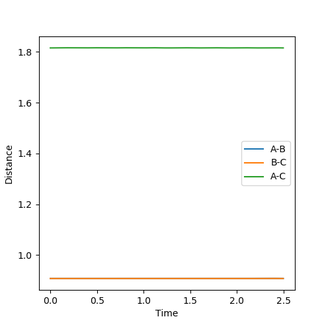
At the transition state there is no force acting on the hydrogen molecule as -∂V(ri)/∂ri=0. Therefore, if you start a trajectory exactly at the transition state with no momentum then it will stay there forever. As Hydrogen is symmetry we can set r1=r2 and set p1=p2=0 to estimate a value for the transition state. By adjusting the bond distance in response to oscillation on the Inter-nuclear distance Vs Time graph, the transition bond length estimated to be a value of 0.9076 Å. This is because no change in the inter nuclear distance over time shows that the atoms are being held in that position. Also, the kinetic energy equals 0 and so this also indicates the transition state had been reached.
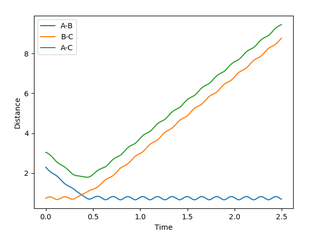
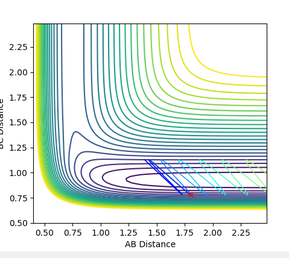
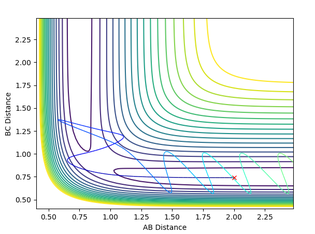
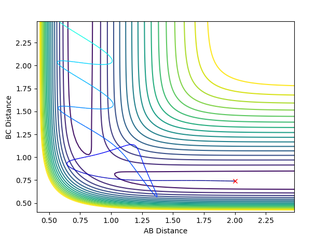
Calculating the reaction path
The reaction path ( minimum energy path) is a trajectory that requires the minimum energy to form the products. This can be mapped from the transition state and can be seen to follow the valley floor. Both this and the dynamic trajectory were run by changing one of the bond distances to 0.9176. The black line seen is the mapped trajectory. The dynamic surface plot shows oscillations of potential energy surface showing that the molecule is vibrating and this agrees with an inertial trajectory whereas the mep trajectory does not show any oscillation which is not an accurate representation of what is actually occurring. Also, the dynamic path shows the full movement hydrogen atom away in the gas phase whereas the mep shows no further movement to get the lowest energy which isn't a realistic account of the motion and is a very slow rate.
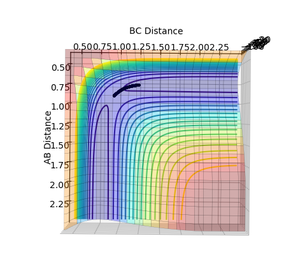
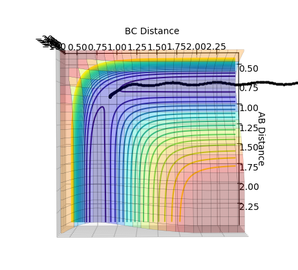
Jas213 (talk) 00:51, 29 May 2018 (BST) If you had increased the number of steps you would have obtained a longer MEP. Why does the MEP show no vibrations energy? Because the momentum is reset to zero at each step.
Reactive and unreactive trajectories
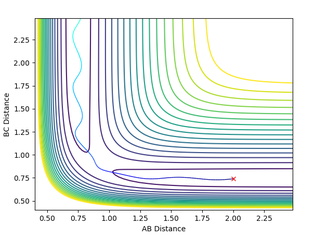
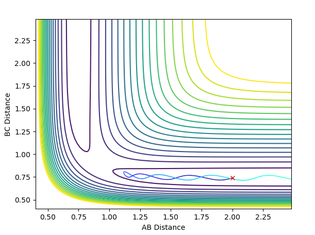
It can be concluded that trajectories within the range r1 = 0.74, r2 = 2.0, with -1.5 < p1 < -0.8 and p2 = -2.5 are reactive. We can also assume that any trajectory with a momenta over the activation barrier will reach completion as they have enough kinetic energy to overcome the transition state and reach product formation. This was tested by using the initial positions r1 = 0.74 and r2 = 2.0 and changing the momenta.
Jas213 (talk) 00:53, 29 May 2018 (BST) Nice intro to your table.
| p1 | p2 | ETotal | React/Non | Contour plot | Discussion | |
|---|---|---|---|---|---|---|
| -1.25 | -2.5 | -99.199 | Reactive |  |
Prior to the transition state, the reaction trajectory is in a straight line and so shows that the BC molecule does not oscillate. The A molecule then attacks the diatomic molecule when it is stationary. The new AB diatomic molecule formed however does oscillate and so does vibrate. | |
| -1.5 | -2.0 | -100.456 | Unreactive |  |
This is an unreactive path as the trajectory does not reach the product channel. This is because the momentum is not high enough to overcome the activation barrier and so the reaction does not reach completion. | |
| -1.5 | -2.5 | -98.956 | Reactive |  |
The BC diatomic molecule oscillates slightly as A approaches but it seems to look like the BC bond length increases closer to when A approaches at the transition state compared to the other reactive trajectory's. | |
| -2.5 | -5.0 | -84.956 | Unreactive |  |
Initially the BC diatomic molecule is not vibrating but once A approaches there is heavy vibration and a triatomic complex appears to form and an AB bond forms. However this doesn't have enough kinetic energy to overcome the barrier and the complex dissociates and A disperses away from the now vibrating BC diatomic and reverts back down the reactant channel . | |
| -2.5 | -5.2 | -83.416 | Reactive |  |
The reaction path again starts with A approaching a non oscillating BC molecule and then another complex is formed but this time it has enough energy to form the products and and the trajectory moves into the product channel. The AB diatomic molecule then has a large amount of oscillation. |
From this investigation we can then see that the previous assumption is not always correct as when p gave a value of -2.5 and -5.2 the reaction became unreactive.
Transition State Theory
Transition state theory is used to explain the rates of reactions and qualitatively how they take place. The three main assumptions are:
1) The reactants and the activated complex are in equilibrium ( quasi equilibrium ) but not the products 2) The reaction trajectory will pass through the saddle point/transition state on the potential energy surface. 3) The reactants nuclei adhere to classical mechanics
Assumption three, assumes that the nuclei obey newtons law's of motion and do not take into account tunneling or the fact that molecular vibrations are quantized as these are quantum mechanical effects and it also doesn't take into account barrier re crossing that can occur as was seen in the table. The complex formed and was high energy but did not produce products, this shows that not all energetic collisions result in product formation but TST assumes this. So, the rates of reaction assumed by TST would be faster than those determined experimentally.
Jas213 (talk) 00:55, 29 May 2018 (BST) Correct, where are your references for TST?
F-H-H system
Reaction energetics
The F + H2 reaction is exothermic because the HF bond is lower in energy ( lower enthalpy) than the H-H bond. Therefore, when the new bond is formed energy is released into the surroundings making the reaction exothermic. Therefore H + HF is endothermic as the H-H bond is higher in energy ( higher enthalpy) than the H-F bond and so when the new H-H bond it has to take in energy from the surroundings making the reaction endothermic.
Jas213 (talk) 00:56, 29 May 2018 (BST) Justifying one being endothermic because the other is exothermic could have been better. You refer to the bond energies, you could have stated explicit values or described the relative height of the channels in the surface plot.
Transition state of reactions
Locating the transition state in this scenario is a little different as the system is no longer symmetric and so we cannot assume that r1=r2. But, the momentum (kinetic energy) is still 0. In an exothermic reaction the transition state most closely resembles the reactants and in an endothermic reaction the transition state more closely resembles the product. So for F + H-H the values weren't moved very far from the original values and the momentum was set to zero and it was found that the transition state was found at H-H 0.7463 and F-H 1.810 angstroms. For the H + HF system, the transition state was found by moving the bond lengths closer to the products which is the same as the reactants in the previous reaction. The same transition state was found as the same complex is formed in both cases; this is a good representation of Hammond's postulate. As can be seen the kinetic energy is zero showing that the transition state has been reached.
Jas213 (talk) 00:58, 29 May 2018 (BST) Nice, good answer.
Activation energy of the reaction
The activation energy is the energy barrier that the reactants have to reach in order to form products. This barrier is difference between the energy of the transition state and the minimum of the reactants. The energy of the transition state was found to be -103.751. the F + H2 reaction was studied. MEP trajectory was undertaken and the bond length was changed towards the formation of FH just slightly (1.80) this gave an energy minima for the reaction to be -133.927, and for the HF + H reaction the same was done and the energy minima was found to be -104.028
Activation energy = Energy of transition state - Energy of reactants
For the F + H2 reaction : -103.751 -(-104.028) = 0.277 Kcal/mol
For the HF + H reaction : -103.751 -(-133.927) = 30.176 Kcal/mol
This makes sense as the HF bond is lower in energy than the H-H bond and therefore the reaction to form the HF bond would have a lower activation energy as the reactant bond (H-H) is of higher energy and so has less energy to gain to overcome the activation barrier. This is the reverse for the other reaction.
Jas213 (talk) 00:59, 29 May 2018 (BST) This is all correct, but not using the MEP approach that was asked for. Consequently, no energy vs. time plots were provided.
Reaction Dynamics
The conditions found to get a reactive trajectory of F + H2 reaction were:
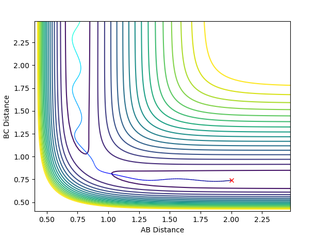
rF-H = 1.81, rH-H = 0.75, pF-H = -0.5 , pH-H = 0.8 This is an exothermic reaction and as discussed previously therefore releases energy into the surroundings, usually as heat energy if we assume no work on the surroundings is being done. This heat energy is released to the surroundings through vibrational motion. We can see this increase in vibrational motion on the contour map clearly as when the HF bond is made it has a high vibrational movement. On the energy Vs time plot we can clearly see that the energy is being conserved as as the potential energy decreases the kinetic energy rises. This could be analyzed through IR spectroscopy to see the high overtone bands produced by molecules with higher vibrational states
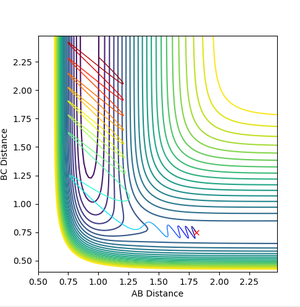
Polanyi's empirical rules
The reactants in a reaction must have enough energy to overcome the activation barrier of a reaction. This energy can be in the form of vibrational or translational. Polanyi's rules state that vibrational energy is better at getting your reactants to overcome a late transition state and they say that translational energy is better at getting your reactants to overcome an early transition state. Therefore for the exothermic reaction, F + H2 , translational energy in the molecule is more effective and for the H + HF reaction, vibrational energy is more effective. (p1=vibrational energy, p2 = translational energy)
Jas213 (talk) 01:02, 29 May 2018 (BST) Where's your citation for polanyi's rules? Would have been better if you had said pHH and pHF, with one and two I can't tell if it's correct, since in the previous example you used pHF and pHH and I don't know which way round you entered the atom labels in the software.
The H + HF reaction is endothermic, therefore according to Hammond's postulate has an early transition state, and so an increase in vibrational energy over translational is more effective. The momenta was set to (p1=1.5, p2 = -0.55). This was then reversed. As can be seen this system does obey Polanyi's rules and a reaction occurs when the vibrational energy is high but not when it is low in respect to the translational energy. This coincides with what it should be for an endothermic reaction.
Jas213 (talk) 01:04, 29 May 2018 (BST) As can be seen where? Which ones of your plots are you referring to? According to your labels they both show the other reaction.
