MRD:MoDyYuhan
Exercise 1
Question 1
Transition state is mathematically defined as saddle point, which is a point at which the slopes in orthogonal direction are all zero but is not a local extremum. It sits at the minimum of one direction and at the maximum of another direction which is orthogonal to each other. While local minimum is the minimum at all directions.
You are given a mathematical description of the saddle point in terms of second partial derivatives. The second partial derivative of a maximum is negative and the second partial derivative of a minimum is positive therefore in the two trajectories the second partial derivative at the saddle point these values are negative and positive in the direction of the reaction coordinate and orthogonal to it, respectively. Rk2918 (talk) 11:07, 20 May 2019 (BST)
Question 2
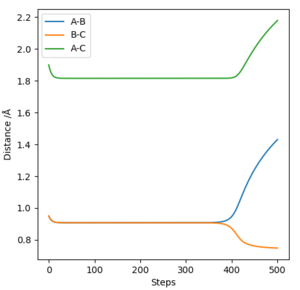
Calculation Type: MEP
AB distance = 0.95
BC distance = 0.95
Momentum of AB and BC is both 0.
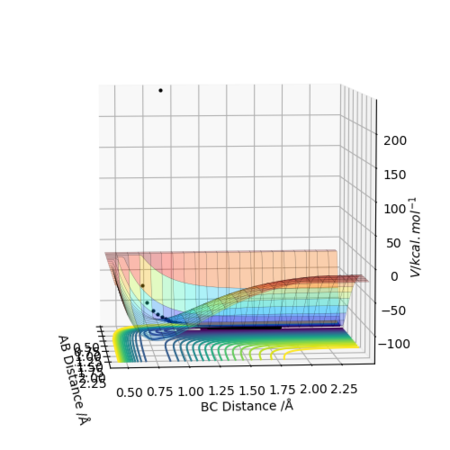
Best estimate of transition state position rts is (0.9074,0.9082).
How can the transition state be at different distances on the two axes when the reaction is symmetric? Rk2918 (talk) 11:09, 20 May 2019 (BST)
The transition state is where A-B is the lowest, same distance of B-C plateau(where the configuration the whole system stays for long time), around 0.907.
Also, half of the A-C plateau distance confirms the data here since the model is symmetric.
See below is the 'Internuclear Distances vs Time' plot for this case.
Question 3
AB Distance = 0.91
BC Distance = 0.907
Both AB and BC momentum is 0.
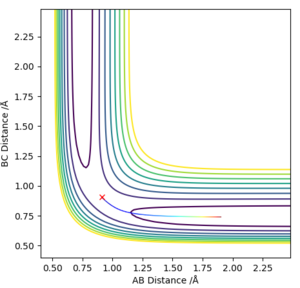
The image on the left is the Contour Plot under MEP calculation type while the right hand side one was calculated under Dynamics. The dynamics calculation gives more wavy path which is more realistic because it takes the motion of atoms during the reaction into account. When we look at the MEP result, the reactive trajectory is a smooth curve, indicating the energy is conserved in an ideal situation.
This isn't quite right. You need to understand that the shape of the Dynamics calculation represents the vibrations of the atoms within the molecule, and how the difference in the calculation methods manifests as such on a potential energy surface. Rk2918 (talk) 11:13, 20 May 2019 (BST)
Question 4
Calculation Type: Dynamics
AB Distance = 0.74
BC Distance = 2
| p1 | p2 | Etot | Reactive? | Description of the dynamics | |
|---|---|---|---|---|---|
| (1) | -1.25 | -2.5 | -99.0 | YES | It finally touches into product region. |
| (2) | -1.5 | -2.0 | -100.0 | NO | There is a trace of transition state, but not enough energy for product to be formed. |
| (3) | -1.5 | -2.5 | -99.0 | YES | It finally touches into product region. |
| (4) | -2.5 | -5.0 | -84.9 | NO | Similar to (2) |
| (5) | -2.5 | -5.2 | -80.9 | NO | It touches into the product region for a while, but goes back to reactant eventually. |
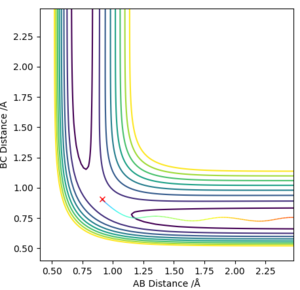
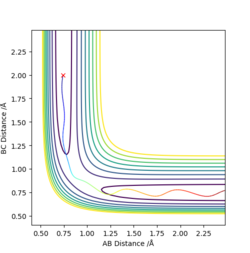
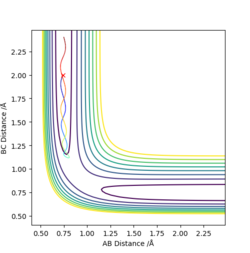
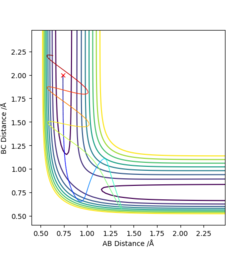
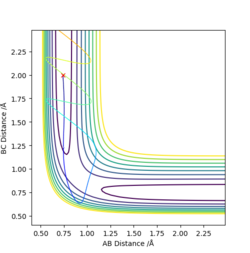
The first two pictures shown above are the contour plots of the (1) and (3) measurements which both indicate a reactive trajectory. The red cross symbol on the graph shows a initial position in potential energy diagram. It first sits at the region within the reagent. Then it moves along the reactive trajectory, ending in the product region(where the BC distance and AB distance are almost reversed) eventually.
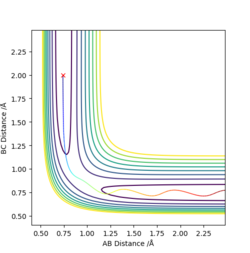
The other three pictures above are of (2), (4) and (5). They are all leading to an unreactive trajectory because the end of the path curve still remains within the reagent region even though the trajectory might touches into the product region, but goes back to reagent region eventually.
Question 5
Main assumptions of Transition State Theory is that the motion of atomic nuclei follows Newton's equations of motion, i.e. obey classical mechanics. In fact, molecular vibrations are quantized and there is still possibilities of quantum tunneling effects.
Transition State Theory would predict the reaction under penultimate set of conditions is unreactive according to the graph of trajectory. However, the experimental values of reaction rate should be non-zero, which means there must be some products formed.
The reasons for the failure of Transition State Theory in this case are there is a chance that molecule will react via tunneling even if they do not collide with enough energy to transverse the energy barrier (which gives a negative result in TST). In addition, tunneling probability increases with decreasing barrier height.
The important thing to understand here is the idea of barrier recrossing. Think about the assumptions TST makes to do with barrier recrossing, and about whether or not barrier recrossing can happen in real reactions. Then think about how this difference can lead to an underprediction or overprediction of the rate of reaction. Rk2918 (talk) 11:15, 20 May 2019 (BST)
Exercise 2
Question 6
E(H-H) = 436 kJ/mol [1]
E(H-F) = 569 kJ/mol [1]
Forward reaction:
Calculation type: MEP
AB Distance = 1.5
BC Distance = 0.75
Both AB and BC Momentum is zero.
F + H2 → H + HF
The bond forming is stronger than the bond breaking so the reaction is endothermic. Therefore, the trajectory on Surface plot goes up, ending up sitting at a less negative potential. The forward reaction should be opposite to the backward reaction.
Backward reaction:
Calculation type: MEP
AB Distance = 0.5
BC Distance = 0.9
Both AB and BC Momentum is zero.
H + HF → F + H2
The reaction is exothermic. Hence, the trajectory on Surface plot goes down, ending up sitting at a more negative potential.
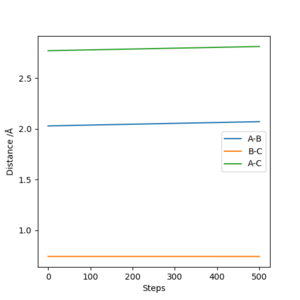
The approximate position of the transition state for both forward and backward reaction is 2.029(AB distance), 0.742(BC distance). This is done by testing the conditions to obtain a graph of Internuclear Distances vs Time, which is shown below. The three internuclear distance is almost constant under this sets of conditions, indicating the existence of transition state.
Question 7
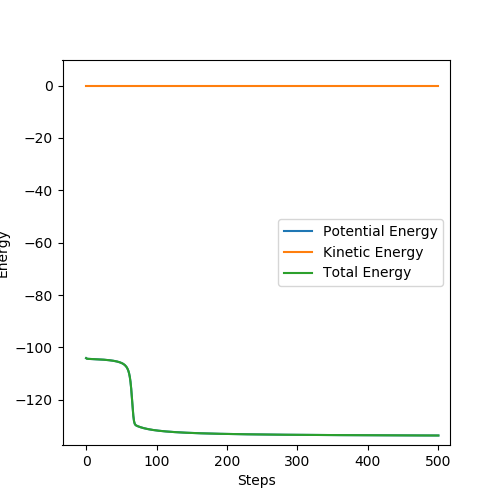
The graph above shows the Energy vs Time under MEP. AB distance is 1.5 and BC distance is 0.74. There is a sudden drop of green line, approximately from -104.4 to 129.6 kJ/mol, giving 25.2 kJ/mol activation energy for the backward reaction.
Question 8
Calculation type: MEP
AB Distance = 1.5
BC Distance = 0.75
Both AB and BC Momentum is zero.
Since energy is conserved, the reaction energy is released via thermal energy. It can be confirmed by observing the change of temperature of the reaction system during the experiment.
Where is the accompanying exercise where you were meant to change the vibrational/translational energy quantities and observe the effects, discussing them in the context of Polanyi's Rules? Rk2918 (talk) 11:17, 20 May 2019 (BST)
Reference
[1] 9.4 Bond Strength and Energy, LibreTexts, [accessed May 2019]