MRD:MOF17
Molecular reaction dynamics lab
H + H2 collisions
Transition state definition
The transition state is defined on a potential surface diagram as a point where the first derivative of the energy with regards to the interatomic distances is 0:
∂V(ri)/∂ri=0
What distinguishes it from saddle points, where the first derivative is also 0, is that the second derivative is negative (positive at saddle points), meaning that the the plot is curving downwards:
∂2V(ri)/∂ri2<0 for maximum
Not true. First derivative is zero, means the gradient is zero. It means, it could be a local minimum, a local maximum or a saddle point. To distinguish between the different points, you need a second derivative. Because it is a 3D plot, you need two planes intercept to each other to define it. A local maximum, the second derivatives in both planes are negative. A local minimum, the second derivatives in both planes are positive. A saddle point, the second derivative at one plane is negative and at the other plane is positive, meaning it is a minimum point at one plane and a maximum point at other plane. Please check the figure.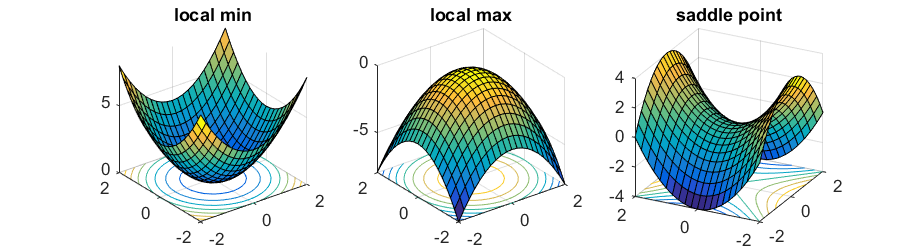 
Sw2711 (talk) 14:32, 24 May 2019 (BST)
Transition state location
From the contour plot the internuclear distances of the transition energy can be roughly estimated to be arouynd 1. aroundSw2711 (talk) 14:48, 24 May 2019 (BST)Moving from this,the internuclear distances plot can be inspected. When the distances are set to the exact transition state internuclear distances, the system will not "roll downhill" by vibrating, and so the plot should show constant internuclear distances, with two degenerate values for A-B and B-C distances and a single internuclear distance twice that value for A-C.
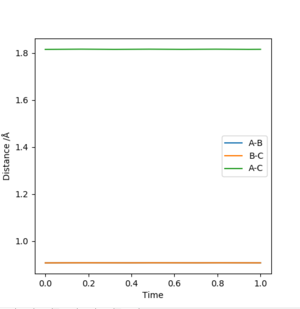
Could you please tell me how you managed to get this plot by setting both distances to 1? I've got this. From your plot, it's not actually 1?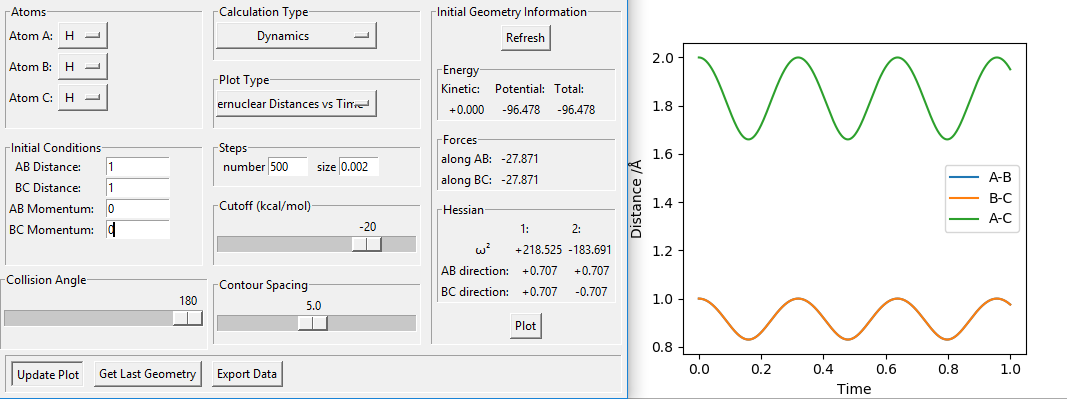 
Sw2711 (talk) 14:46, 24 May 2019 (BST)
Trajectory calculation
If one of the A-B or B-C distances is kept at the transition state distance while the other is changed slightly (e.g. 0.01 A), the system will have moved slightly from the transition state slightly, and will now move towards a state where the atoms with initial transition state internuclear distance will compose a molecule, while the initially incrementally larger distance will keep increasing to result in a free atom. Two different types of calculations can be run for this trajectory. In the first, the MEP trajectory, the momenta are reset to 0 after each step, so any vibrations that would arise from the initial conditions will not be shown, and the path taken will equal the minimum energy path. This equal energy path simply follows the bottom of the surface energy plot, resulting in a smooth line constantly moving downhill and never 'up' any of the contours.
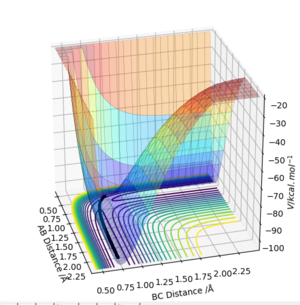
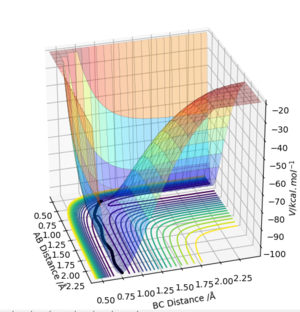
The second trajectory calculated is the dynamic trajectory, which shows a more realistic picture of what happens to the system moving from the transition state to the products. The line shows vibrations, with periodic variations in the BC internuclear distance. The observations above are confirmed by the internuclear distance plots.
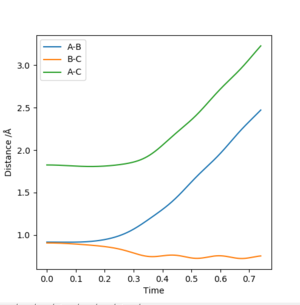
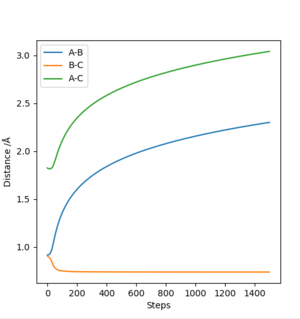
This part is good Sw2711 (talk) 15:08, 24 May 2019 (BST)
Determining reactive trajectories
| p1 | p2 | Etot | Reactive? | Description of the dynamics | Illustration of the trajectory |
|---|---|---|---|---|---|
| -1.25 | -2.5 | -99.018 | yes | This low energy trajectory can be seen to move towards the transition state without much vibration in the H2 molecule, whereupon the collision takes place and the new B-C molecule is vibrating slightly as it moves away from hydrogen A. |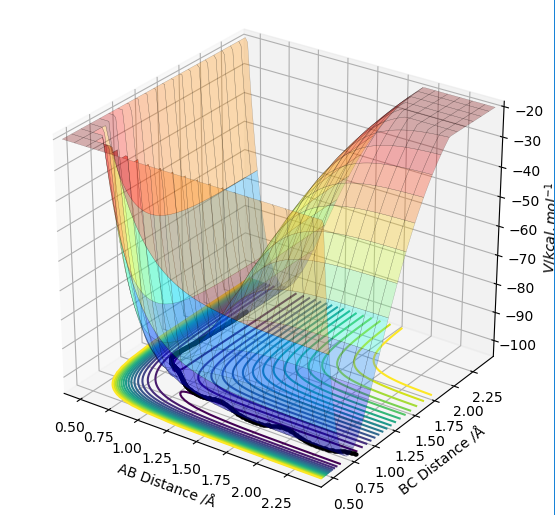 
|
| -1.5 | -2.0 | -100.456 | no | The overall energy in this trajectory is lower and we can see that there is already vibration in the A-B molecule approaching the transition state. The kinetic energy does not appear to be high enough to reach the transition state, owing to the lower difference in the momenta of the molecule and the atom in this case. Therefore the system returns back to its starting reaction coordinates without forming a new molecule. |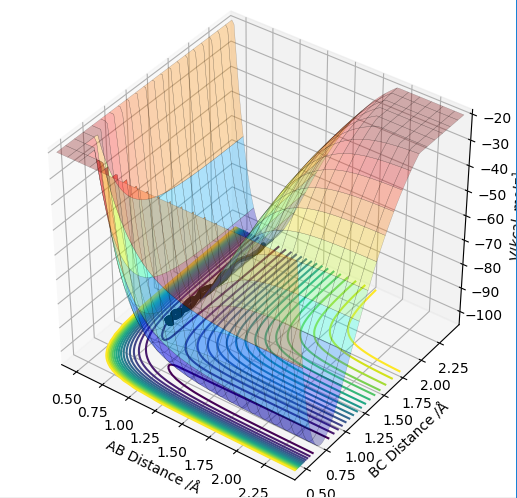 
|
| -1.5 | -2.5 | -98.956 | yes | Relative to the last trajectory this system is much higher in energy. As in the first case, the trajectory is reactive, with the main difference that there is, like in the second case, some vibration present already in the A-B molecule before the transition state. Following collision, the newly formed B-C molecule has a higher vibrational frequency than the original molecule. |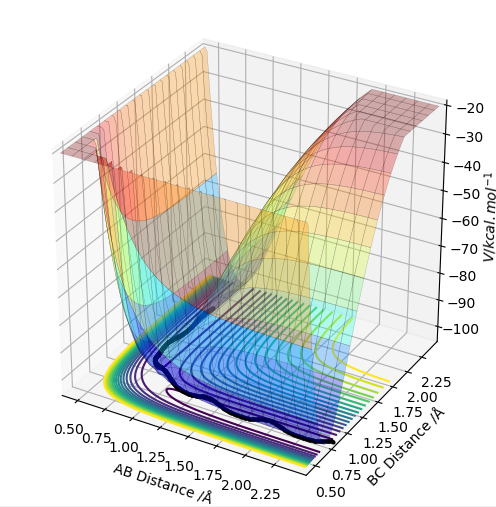 
|
| -2.5 | -5.0 | -84.956 | no | The vibrations of the A-B molecule are much higher in energy than in any of the trajectories before. This means that when the system passes over the point of the transition state, and the B hydrogen atom moves from the molecule A-B to molecule B-C, the vibratios cause this newly formed molecule to immediately dissociate and the original A-B molecule reforms. This is why the surface plot seems to "curve around" the minimum energy pathe and then circle baclk to the reactant coordinates. Good, just to tell you a term. TS recrossing Sw2711 (talk) 15:14, 24 May 2019 (BST) |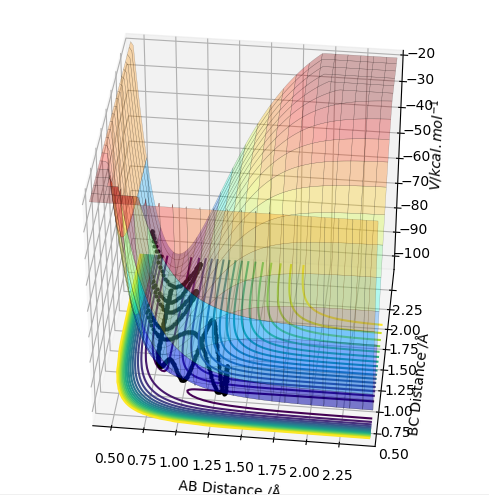 
|
| -2.5 | -5.2 | -83.416 | yes | This highest energy system has a reactive trajectory, as the particles move into the product channel. Due to the high energy oscillations the trajectory is very complex around the transition state, with the hidrogen atom being 'passed around' the original and newly forming molecule. The product shows very high energy oscillations. |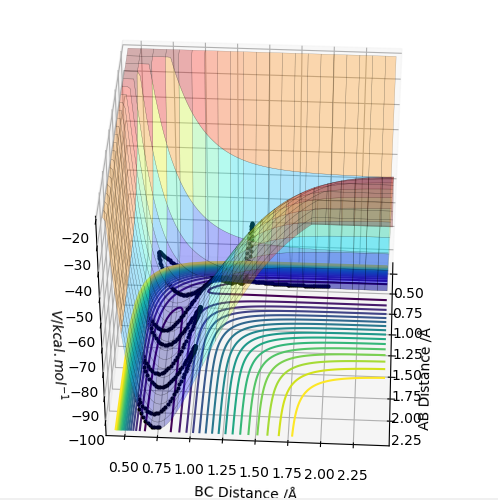 
|
From the table we can conclude that the energy that the H + H2 system possesses is not the only factor in influencing whether the reaction will go to completion. For example, the energy increased from example 3 to example 4 and yet the reaction did not go to completion. This suggests that the distribution of energy between its different forms in the system is also very important. GoodSw2711 (talk) 15:14, 24 May 2019 (BST)
Transition state theory makes several assumptions. The first is that it assumes the Born-Oppenheimer approximation holds and therefore neglects quantum tunneling. The second assumption is that the reactants have a Boltzmann energy distribution. The third is that a system which has moved from the reactants to the transition state will not break down to form the products again, but will always go to the reactants.[1] Did you swap the 'reactants'
In the case of this last assumption, the examples in the table above clearly show that it is not true. We can see that the system can cross the activation barrier only to re-cross it again and move back towards the products. The simple case of only having to cross an activation barrier therefore does not always hold true. In such cases the rate of reaction calculated using TS theory would be higher than the actual rate due to not accounting for re-crossing.
I'll assume you understand this part, because the last paragraph. Moreover, any statements talking about 'distribution' is not very applicable here, as we only have three atoms in our system. Sw2711 (talk) 15:54, 24 May 2019 (BST)
H + H2 collisions
Energetics of the reaction
By inspecting the potential energy surface we can see that the F + H2 reaction is exothermic, as the product channel is much lower in energy than the reaction channel. For the HF + H reaction the opposite is true and the reaction is endothermic. This is because of how electronegative the fluorine atom is, and the resulting strength of the F-H bond, whose energy of formation far outweighs the energy of dissociation of the hydrogen molecule. In the opposite direction, the energy released be forming a new H-H bond is not nearly enough to compensate for the breaking of the H-F bond. GoodSw2711 (talk) 15:54, 24 May 2019 (BST)
Locating the transition state coordinates
Hammond's postulate states that a transition state will most closely resemble the species which are energetically closest to it (this may be the reactants or the products). As energy differences usually entail bond formation and molecular rearrangements a small energy difference means a close structural similarity. For exothermic reactions the transition state resembles the reactants and for an endothermic reaction it most closely resembles the products. Using this knowledge, a transition state was sought in the reactant channel of the F + H2 reaction, and the distances were found to be: c ???what? Sw2711 (talk) 15:55, 24 May 2019 (BST)
Activation energies of system
By producing an MEP plot in the way of moving the F-H internuclear distance slightly in the direction of either the products or the reactants, the minimum energy path can be followed in both directions. In this manner the energies of the reactants, products, and transition state were respectively found to be: How did you use an MEP plot? You need to show me.Sw2711 (talk) 15:56, 24 May 2019 (BST)
EF, H2 = -103.980 kJ/mol
EFH, H = -133.923 kJ/mol
Etransition state = -103.752 kJ/mol
The activation energy is then simply subtracting the transition state energy from the energy of the reactants in both directions of the reaction:
Eact, exo = 0.228 kJ/mol
Eact, endo = 30.171 kJ/mol
Release of reaction energy
This part is good. Sw2711 (talk) 15:58, 24 May 2019 (BST) The reaction conditions which led to a reactiove trajectory in this case were:
rF-H =2 A, rH-H =0.8 A
pF-H =-1, pH-H =-0.1
Since the reaction is exothermic, it means that the products in their ground state will have a lower energy than the reactants in their ground state. But since conservation of energy states that energy cannot be created or destroyed, it means that potential energy difference between the reactant and product levels must be converted into some other forms of energy - this extra kinetic energy is evident in the products as an increase in translation, rotation and vibration. The much higher oscillations of the F-H molecule relative to the reactant H-H molceule are evident in the graph below.
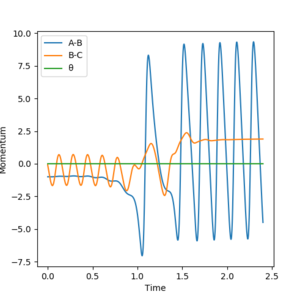
The higher vibrational energy of the molecule could be detected in the form of an IR spectrum where molecules populating higher vibrationa states would produce hot bands in the spectrum. To confirm that the reaction is exothermic calorimetry could be used.
Polanyi's rules and the FHH system
This part is goodSw2711 (talk) 16:02, 24 May 2019 (BST) Polany's rules give us some direction into how to distribute the energy over a system of particles in order for a reaction to go to completion. They state that for an endothermic reaction, the late transition barrier is easier overcome with excess vibrational energy, whereas for an early transition - exothermic reaction - it states the barrier will be more easily overcome with translational energy. [2]
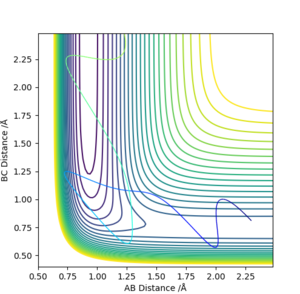
Since the F + H2 reaction is exothermic and, according to Hammond's postulate, has an early transition state, an excess of translational energy should lead to a reactive pathway. Considering pF-H as correlating to translation energy and and pH-H to vibrational energy in this reaction, we can set up the two trajectories seen below.
pF-H = -5.8, pH-H =1
pF-H = -1, pH-H =-4
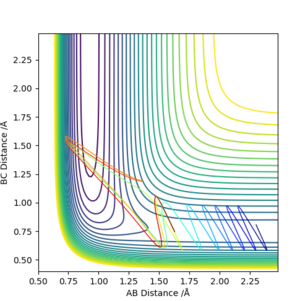
We can see that Polanyi's rules hold true. The system where the momentum the two molecules approaching each other was higher - and therefore the translational energy higher than the vibrational - had a reactive trajectory whereas the other did not.
For the opposite reaction, the opposite should be true. FH + H is an endothermic reaction and so the transition state is late, meaning that vibrational energy will be more effective in overcoming it. In this case pF-H correlated to vibrational energy and pH-H to translational energy.
pH-H = -3, pF-H =1
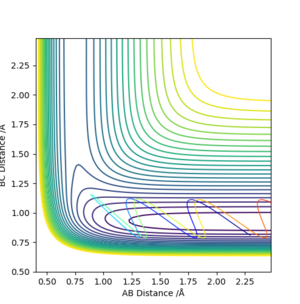
pH-H = -0.5, pF-H =6.5
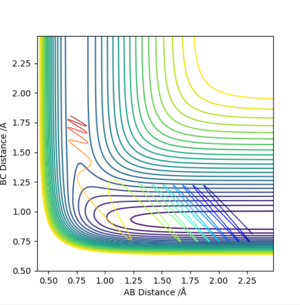
Once again the rules hold true. The system with higher vibrational energy has a reactive trajectory whereas that with excess translational energy does not.
References
- ↑ T. Bligaard, J.K. Nørskov, Chapter 4 - Heterogeneous Catalysis, Chemical Bonding at Surfaces and Interfaces, Elsevier, 2008
- ↑ Z. Zhang, Yong Zhou, et. al., Theoretical Study of the Validity of the Polanyi Rules for the Late-Barrier Cl + CHD3 Reaction The Journal of Physical Chemistry Letters, 2012, 3 (23), 3416-3419