MRD:ML9418

Dynamics of the Reaction H₂ + H -> H + H₂

The Transition State and its Identification

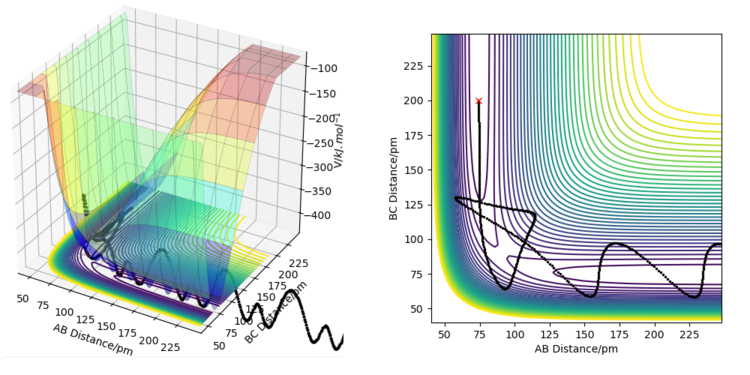
The transition state on a potential energy surface diagram is defined as the point where the gradient of the potential ∂V(r_i)/∂r_i is zero in all directions. It is the point with the highest energy on the minimum energy path that connects the reactants and the products.

For a symmetric potential energy surface, the transition state lies on the diagonal line where r₁=r₂. It is the point on that line with the lowest potential energy. The exact location of the transition state for a reaction with a symmetric potential energy surface can be found by running a minimum energy path simulation starting from a point where r₁ = r₂. The point where that minimum energy path stops is the transition state.

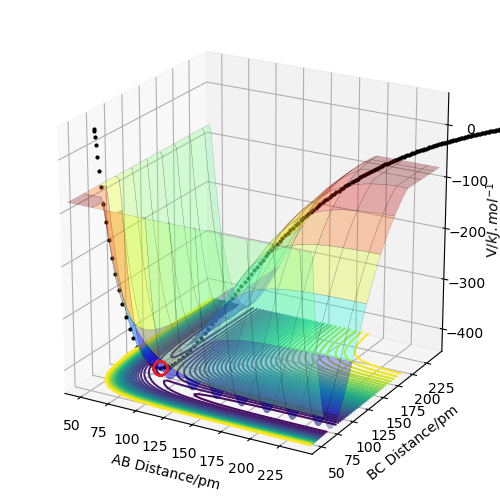
Figure 1: potential energy surface plot of H_a-H_b + H_c -> H_a + H_b-H_c, where the diagonal r₁=r₂ line is dotted in black and the transition state is circled in red

A transition state is different from a local minimum due to the fact that it is a saddle point, meaning the surface around it has negative Gaussian curvature. This means that the maximal and minimal values of curvature (the second derivatives) around the transition state are of opposite signs, meaning they curve in opposite directions (up and down). A local minimum, on the other hand, has positive Gaussian curvature, meaning that the curvature is in the same direction all around (up in this case).

good use of a figure to illustrate your point. Be careful with your definition here, the saddle is defined as both a minimum (in one reaction) and a maximum (in another orthoganol to the first direction), this relative direction applies to the second partial derivative. Be careful too, in that these derivatives are partial, in that they are with respect to an aspect of the PES. Rs6817 (talk) 17:02, 4 June 2020 (BST)

The Position of the Tranition State for the Reaction H₂ + H -> H + H₂

For the reaction H₂ + H -> H + H₂, the transition state is at a point where the distances between neighboring hydrogen atoms are around 90.774 pm. This point was found using the method mentioned before - a minimum energy path simulation was run, starting from a point on the diagonal r₁ = r₂ line. The point where the minimum energy path simulation stops is the transition state, because it is the minimum energy point along the r₁ = r₂ line. It can not move any lower (towards the reactants or the products) because at that point the gradient is zero in all directions, including the minimum energy path that connects the reactants and products.

Figure 2: internuclear distances of hydrogens for the aforementioned reaction plotted against processed steps. This plot was constructed by simulating a minimum energy path from a starting point where r₁ = r₂ = 60 pm

Ok, what were the initial conditions ? You havnt yet introduced MEP as a concept. Rs6817 (talk) 17:12, 4 June 2020 (BST)

The Minimum Energy Path (MEP)

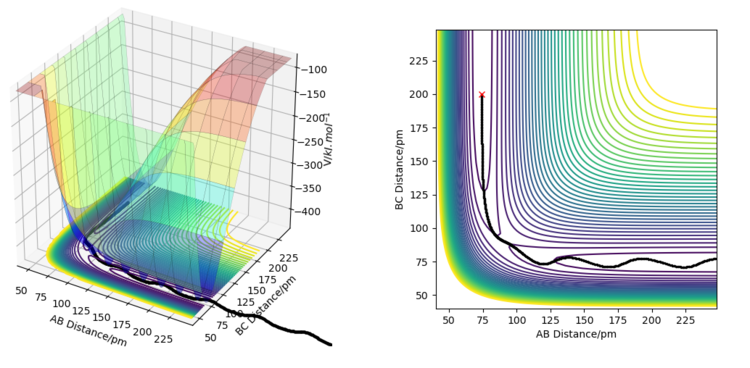
The minimum energy path, or reaction path is a theoretical reaction trajectory that corresponds to infinitely slow motion of reactants and products. On an MEP, the momenta and velocities are always zero, because the movement of reactants and products is stretched on an infinitely long timescale. The MEP is different from the actual reaction trajectory because on the MEP, the system has no kinetic energy and the potential energy always goes down (unless the MEP is specifically connecting two points on the surface, such as the reactants and the products). This means that the system is always losing total energy to head directly to the point of lowest potential energy. In reality, total energy must always be conserved, so when the trajectory heads downward on the potential energy surface (losing potential energy), it must gain kinetic energy. This can be in the form of translational, rotational, vibrational, or electronic energy. For the given reaction, when an MEP is simulated from a point where r_bc = r_ab + 1 = r_ts + 1, the trajectory heads straight towards the H_a-H_b + H_c products along the trough of the valley, whereas when a dynamics simulation is run from the same starting position with 0 momentum, the trajectory clearly shows some vibration between H_a and H_b. This shows that as potential energy is lost, kinetic energy is gained in the form of vibrational energy, in order to conserve total energy.

Very well explained. Well done. Please try to refer to figures as you use them in the text. Rs6817 (talk) 17:16, 4 June 2020 (BST)

If the simulations were run under the conditions r_ab = r_bc + 1 = r_ts + 1, the trajectory would lead to the H_b-H_c + H_a products instead of the H_a-H_b + H_c products.
If the initial and final conditions of the simulations are reversed (initial position on the plot replaced by the final position from the previous simulation, and initial momenta replaced by the final momenta), one ends up with a trajectory that starts from where the previous simulation ended, and ends ar where the previous simulation started. In this case, the trajectory ends exactly at the transition state, and where it starts depends on how many steps the previous simulation was run for.

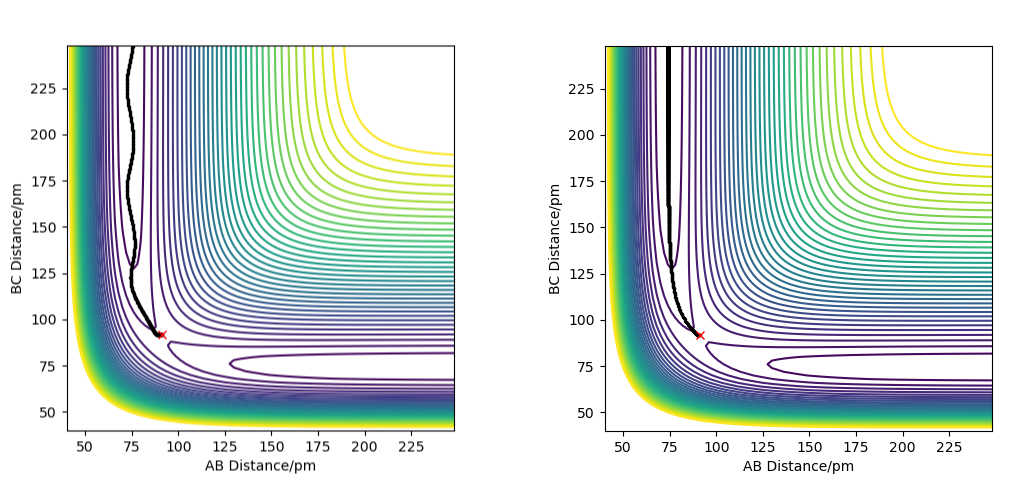
Figure 3: a comparison of the MEP (right) and the actual reaction path (left) on contour plots, where both paths start from a point that is minimally deviated from the transition state (r_bc=r_ab+1=r_ts+1)

Testing Different Reaction Trajectories for the Reaction H_a-H_b + H_c -> H_a + H_b-H_c

Running a reactive simulation for this reaction gives the values of momenta required for the reaction to occur. For r_ab = 74 pm and r_bc = 200 pm, the required value for the momentum p₁ of H_a-H_b is between -3.1 and -1.6 g.mol^-1.pm.fs^-1 and the required value for the momentum p₂ of H_b-H_c is -5.1 g.mol^-1.pm.fs^-1. It might seem a fair assumption that all trajectories with the same starting positions, but with higher values of momenta than the minimum required values, would result in the reaction going through to the products, since they would have enough kinetic energy to pass the activation energy barrier. To test this assumption, a table has been constructed where various values for momenta have been tested with the same starting positions r_ab = 74 pm and r_bc = 200 pm.

Great introduction Rs6817 (talk) 17:19, 4 June 2020 (BST)


p₁/g.mol^-1.pm.fs^-1	p₂/g.mol^-1.pm.fs^-1	E_tot/ kJ.mol^-1	Reactive?	Description of the dynamics
-2.56	-5.1	-414.28	Yes	H_a-H_b is in the vibrational ground state, H_c approaches the molecule directly and forms H_b-H_c, which is vibrationally excited. H_a drifts away from H_b-H_c. Path crosses the activation energy barrier once
-3.1	-4.1	-420.08	No	H_a-H_b is in a vibrationally excited state, H_c approaches but is unable to displace H_a, and drifts away from H_a-H_b. Path does not cross the activation energy barrier.
-3.1	-5.1	-413.97	Yes	H_a-H_b is in a vibrationally excited state, H_c approaches and displaces H_a to produce a vibrationally excited H_b-H_c. H_a drifts away from H_b-H_c. Path crosses the activation energy barrier once.
-5.1	-10.1	-357.2	No	H_a-H_b is in the vibrational ground state. H_c approaches and displaces H_a to produce a vibrationally excited H_b-H_c, but H_a then displaces H_c to produce H_a-H_b once again. H_c drifts away from the vibrationally excited H_a-H_b. Path crosses the activation energy barrier twice.
-5.1	-10.6	-349.4	Yes	H_a-H_b is in the vibrational ground state. H_c approaches and displaces H_a to produce a vibrationally excited H_b-H_c, but the repulsion between H_b-H_c overcomes the attraction and forces H_b and H_c to separate. H_a then approaches H_b to produce H_a-H_b once again. H_c then approaches and displaces H_a a second time to produce a vibrationally excited H_b-H_c. H_a drifts away from the vibrationally excited H_b-H_c. Path crosses the activation energy barrier three times.

The results from these simulations show that not all trajectories starting from the same positions are reactive, even those that have larger momenta than required. The right combination of momenta is needed for a reaction to occur.

Great the table is really clearly explained, well done. Rs6817 (talk) 17:20, 4 June 2020 (BST)

Transition State Theory

Transition State Theory tries to predict the rate constant for a reaction based on the properties of the reactants and the structure of the transition state. It is based on an assumption that all trajectories along the reaction coordinate with a kinetic energy higher than the activation energy will be reactive. However, as we determined from the previous tests, it is possible for the reaction trajectory to pass the activation energy barrier to form products briefly, but then cross the barrier once more to form the reactants again. It is even possible for the trajectory to cross the activation energy more times, but in half of these cases, products will not be formed in the end. In those cases, the trajectory is not reactive, even though it has enough kinetic energy to overcome the activation energy barrier.
For this reaction, there is also a possibility for the reaction to occur without having enough kinetic energy to pass the barrier. This is possible due to quantum tunneling, which can occur in very light particles. The hydrogen atom, however, is not light enough for this tunnelling to occur frequently enough to overcome the reduction in rate that is caused by the possibility of recrossing the activation energy barrier. The fraction of trajectories that are reactive due to tunnelling is orders of magnitude lower than the fraction of trajectories that are unreactive due to bad momenta combinations. This means that the actual rate of reaction will be smaller than the one determined by Transition State Theory.
Another assumption of TST is that a Maxwell-Boltzmann equilibrium is maintained in both the reactants and products. However, in bimolecular gas reactions, such as this one, this does not hold true, since selective energy consumption and release takes place^[1].

You say half of the cases - where does this information come from? What do you mean by this? 'Not light enough' - do you too light to occur? Unclear. Otherwise well answered and plenty of detail Rs6817 (talk) 17:23, 4 June 2020 (BST)

Dynamics of the Forward and Backward Reactions of F + H₂ -> HF + H

The Energetics of the Reactions

The forward reaction for this transformation is exothermic, whereas the backward reaction is endothermic. This is visible on the surface and contour plots below, as the forward reaction products are lower in potential energy than the reactants. This is because the H-F bond is stronger (565 kJ/Mol) than the H-H bond (432 kJ/mol), making the products HF and H more stable than the reactants H₂ and F.

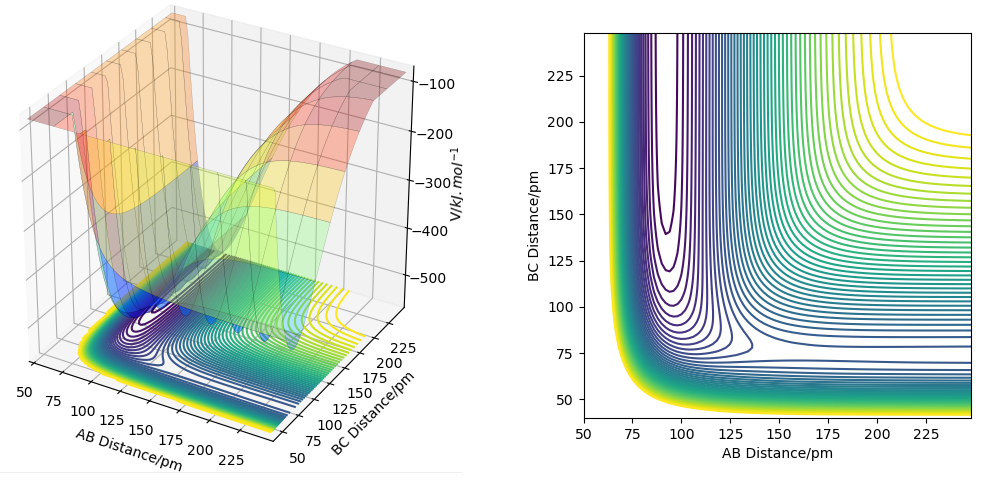
Figure 4: potential energy surface (left) and contour plot (right) for the reaction, where A is the fluorine atom, and B and C are the hydrogen atoms

Ok, where do those values for bond enthalpies come from? Are they calculated directly or are they referenced? Make sure to make this clear. Question is otherwise well described and good use of figure, again would be much clearer if the figures are reference din the text. I.e. Figure X tells us Y.Rs6817 (talk) 17:25, 4 June 2020 (BST)

The Transition State of the Transformation

The location of the transition state is approximately AB = 181.1 pm and BC = 74.5 pm (distance between hydrogens is 74.5 pm and distance between fluorine and closest hydrogen is 181.1 pm). This value is approximate, since it was found by guessing values until the MEP simulation stayed in approximately the same location for 100 steps of 0.1 fs.

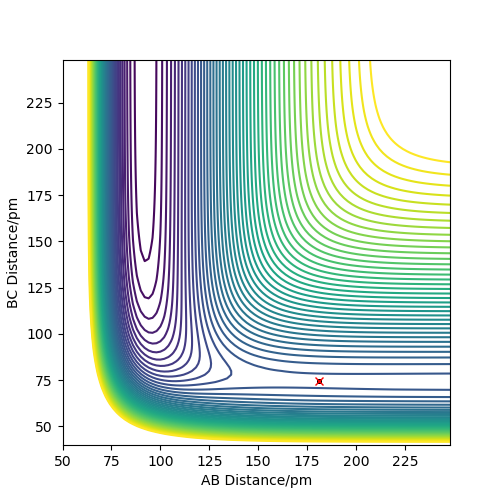
Figure 5: transition state of the reaction displayed on a contour plot

Ok, you have used this MEP method again, which has yielded a good result. However, further information is required here. What do the forces along the bond tell us? What about the Hessian matrix? Either of these properties would have allowed you to assess the quality of your estimation. Rs6817 (talk) 17:26, 4 June 2020 (BST)

The Activation Energies of the Forward and Backward Reactions

The activation energy for the forward reaction is ~1.05 kJ/mol and for the backward reaction it is ~126.67 kJ/mol. These energies were determined by running an MEP simulation from the transition state to the reactants and the products for 8000 steps of 0.2 fs, then estimating where the minimum potential energy plateau would be on an energy against time plot, then subtracting that plateau's value from the transition state's potential energy value. A more accurate value for the plateaus could have been determined by running the simulation for at least twice as many steps, but processing that many steps would take a long time. Using this method gives the activation energy for the reactants approaching from infinitely far away. In a solution or container of finite volume, the activation energy would be slightly lower.

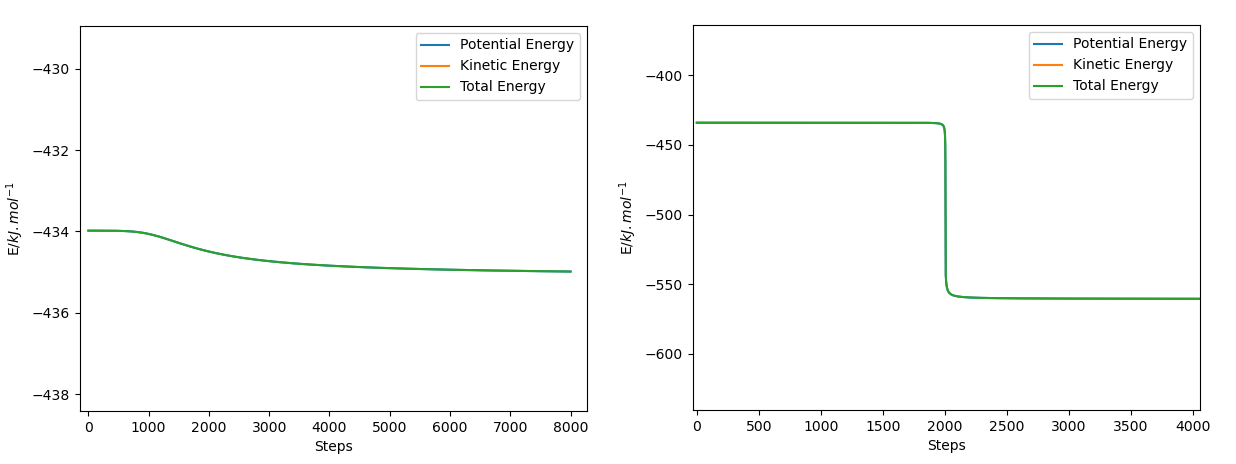
Figure 6: energies plotted against processed steps for going from the transition state to the reactants (left) and to the products (right). This is from an MEP simulation, not a dynamics simulation. The activation energy is the difference between the minimum and maximum energy plateaus

This is a good answer. Rs6817 (talk) 17:27, 4 June 2020 (BST)

Release of Reaction Energy

For the forward reaction, which is exothermic, the products have less potential energy than the reactants. Because total energy must always be conserved, this means that the products must have a higher kinetic energy than the reactants. Kinetic energy can be in the form of translational, rotational, vibrational, and electronic energy. In the forward reaction, potential energy is converted to kinetic energy in the form of vibrational motion. This is shown on the figure below.

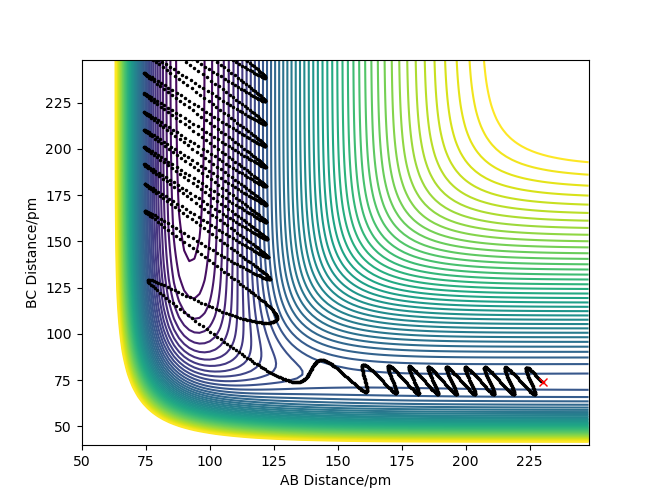
Figure 7: contour plot of the forward reaction, where the starting positions are AB = 230 pm, BC = 74 pm, p₁ = -2 g.mol^-1.pm.fs^-1, and p₂ = 2 g.mol^-1.pm.fs^-1

To confirm whether the reaction energy is being released vibrationally, one could probe the reaction via IR spectroscopy. If the reaction energy is not converted to vibrational energy, all the product molecules in the reaction would be in the ground state. An IR spectrum, in this situation, would only display the peaks going from the ground state to higher vibrational energy states. However, if the reaction energy does get converted to vibrational energy, some of the molecules would populate higher vibrational energy levels, and an IR spectrum would also show peaks going from the higher energy states to even higher energy states. Those peaks are called hot bands. Since the differences between neighboring energy levels for an anharmonic oscillator become smaller at higher energy levels, an IR spectrum would show smaller hot bands that are slightly shifted to smaller wavenumbers from the main peaks. If many IR spectra were taken throughout the reaction, one would at first see hot bands along with the main peaks, then the hot bands would shrink and the main bands grow as the product molecules relax to the ground state.
Another way to determine whether vibrational excitation is occurring is to probe the reaction using infrared chemiluminescence. This is a technique for detecting changes in infrared emission during a reaction, which gives information about the energy states of the products of a reaction^[2]. If infrared radiation is detected from the reaction, it means that potential energy does get converted to vibrational motion. This works because vibrational relaxation, if it is radiative, emits infrared radiation.

Good answer again, well done. You could have potentially mentioned a calorimetry experiment Rs6817 (talk) 17:38, 4 June 2020 (BST)

Effect of Translational and Vibrational Energy on the Reaction

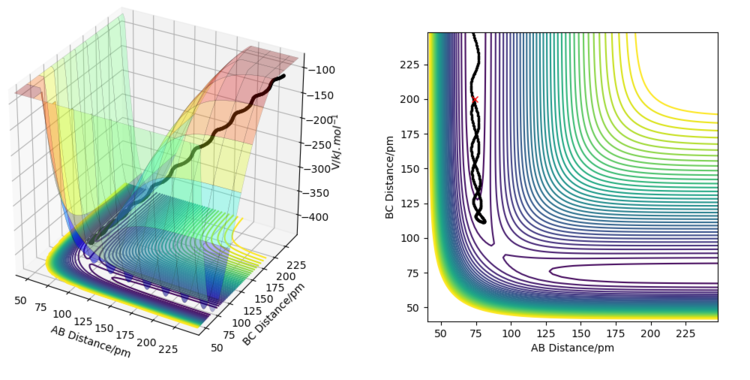
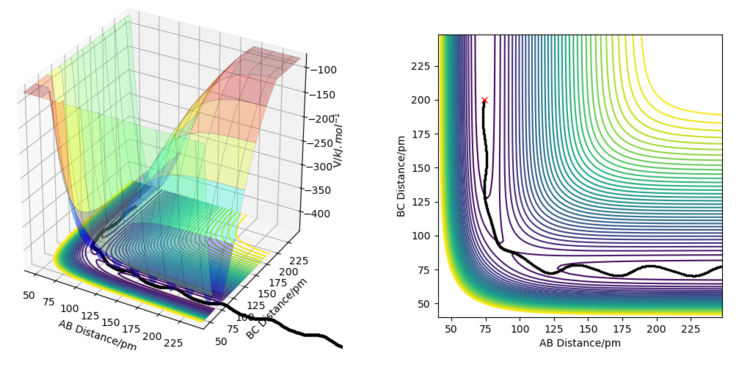
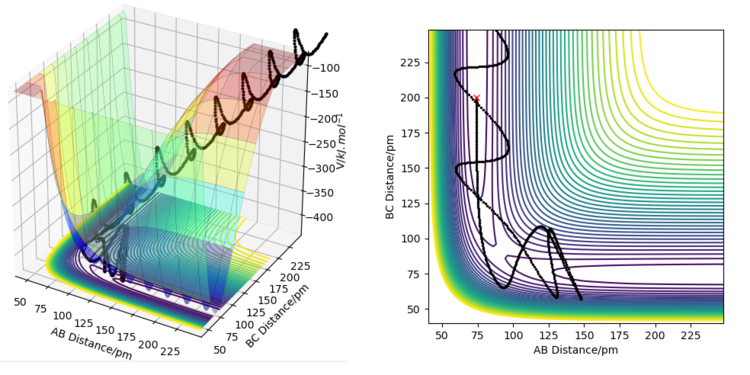
Running dynamics simulations for the forward and backward reactions using various values for the momenta p₁ and p₂ reveals some information about whether vibrational or translational motion is needed for each reaction to occur. For the forward reaction, most trajectories that led to products started with the reactants having low vibrational energy. Conversely, for the backward reaction, large vibrational energy was needed to convert reactants to products. For the forward reaction, there was more leeway for choosing the values of momentum than for the backward reaction. Finding a reaction path for the backward reaction proved difficult, as the vibrational motion needed to be just right for the activation energy barrier to be crossed.
For the forward reaction, very small values for initial momenta can be used, since the activation energy barrier is very small, whereas the backward reaction needs large momenta to occur. This indicates that the required distribution of kinetic energy between translational and vibrational motion is different in an exothermic reaction and an endothermic reaction.
For an exothermic reaction, where the products have a lower potential energy than the reactants, and the activation energy is small, it is better to have less vibrational energy and more translational energy. This is because the activation energy barrier is small and the transition state is directly ahead of the reactants on the potential energy surface plot. This means that the barrier can be easily overcome with enough translational motion, and then the trajectory will just fall into the lower energy products area. Having excess vibrational motion, in this case, could prevent the reaction from occurring because the movement of the vibrational motion on the potential energy surface plot is in a different direction than the minimum energy path. Because of this, excess vibrational energy will cause the trajectory of the reaction to move back and forth up the valley. At the transition state, this can increase the energy barrier that needs to be overcome, and might cause the trajectory to simply fall back towards the products.

For an endothermic reaction, the products have higher potential energy than the reactants and the activation energy is large. On a potential energy surface, the transition state is also not directly ahead of the reactants, but is rather behind the valley's corner, so approaching it directly requires a very large energy barrier to be overcome. Vibrational motion is more useful in this case because it does not move along the minimum energy path, and if the vibrational motion is timed right, it can more easily overcome the large activation energy barrier. This is because if the timing of the vibrational motion is right, the direction of the trajectory will curve behind the valley's corner in the exact right way for the trajectory to be heading directly towards the transition state. The effect of these conditions is illustrated on the figures below.

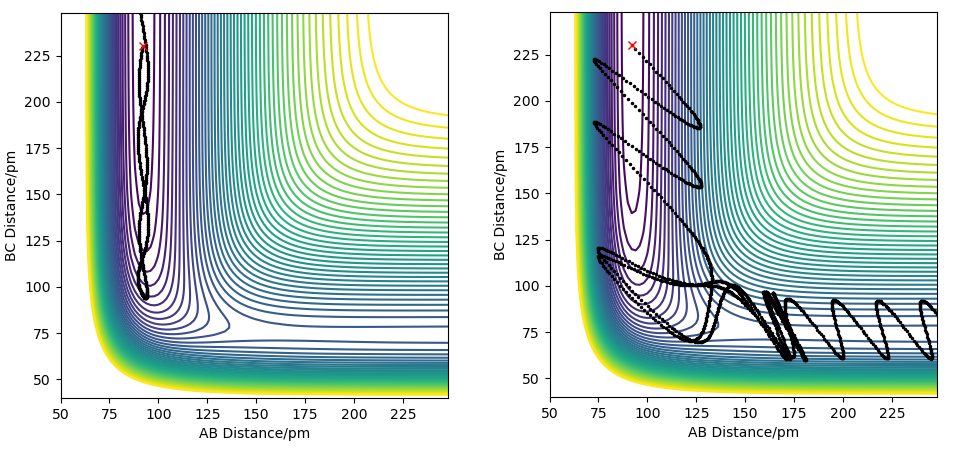
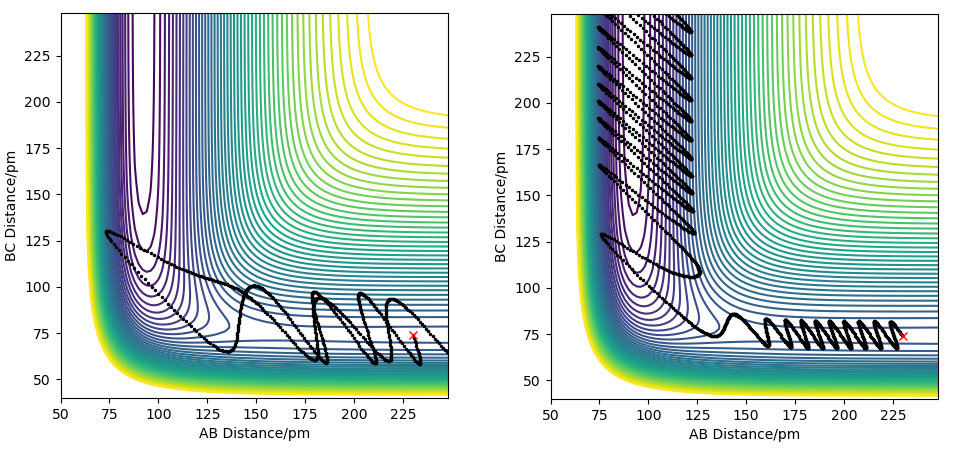
Figure 8: an unreactive trajectory (left) with high translational energy but low vibrational energy, and a reactive trajectory (right) with low translational energy but high vibrational energy. These plots are for the endothermic reaction H + HF -> F + H₂

Figure 9: an unreactive trajectory (left) with high vibrational energy but low translational energy, and a reactive trajectory (right) with low vibrational energy and also low translational energy. These plots are for the exothermic reaction F + H₂ HF + H

Your explanation here is strong, but could do with a reference for where the information is coming from. You needed to make the argument a bit clearer here. The question was in reference to Polanyi rules which explain the relative early and late TS contributing to a dependency on vibrational or trnaslational energies, this also relates to Hammonds postulate etc.. Setting up the argument around these rules first would have lead to enhanced discussion. You also have framed the example around 4 examples (2 for each reaction direction) and a few more would have helped with the conclusions. It is uncelar what the values of the vibrational energy are (outside of assessing these from the figure), quantitative assessment may have helped the comparison betwen vibrational and translational contributions to the reactivity.Rs6817 (talk) 17:43, 4 June 2020 (BST)

References

1)Steinfeld, J. I.; Francisco, J. S.; Hase, W. L. Chemical Kinetic and Dynamics 2nd ed., Prentice-Hall, 1998. pp. 316-318
2)A Dictionary of Chemistry, 6th ed.; Oxford University Press, 2008.

Dynamics of the Reaction H2 + H -> H + H2