H-H-H

What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure?

A minimum on the a potential energy surface will have a negative gradient on one side and a positive gradient on the opposite, That could be a maximum too? --Sw2711 (talk) 15:34, 31 May 2018 (BST)or in other words a positive curvature, A positive curvature I think gives you a maximum--Sw2711 (talk) 15:34, 31 May 2018 (BST) in the direction of one of the axis. Along the other axis it will have a curvature equal to or greater than 0. A transition structure will have a positive curvature perpendicular to a negative curvature. It is not necessarily perpendicular--Sw2711 (talk) 15:34, 31 May 2018 (BST) These curvatures will not fall parallel to the axis as they did with the minimum structure. They will be relatively close to a 45 degree angle to each axis as that bisects the minimum structures that it is transitioning between did you finish your sentence here?--Sw2711 (talk) 15:34, 31 May 2018 (BST)

Overall, I am not sure whether you understand the concept thoroughly. But you demonstrated that you have to look at two different directions to determine a saddle point (a TS). I have left some comments in your answers. Please also watch this video. Hopefully this helps with your understanding. video--Sw2711 (talk) 15:34, 31 May 2018 (BST)

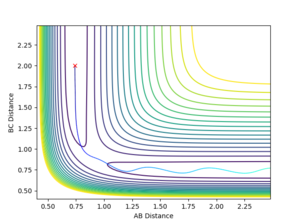
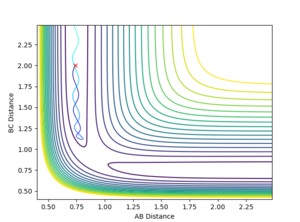
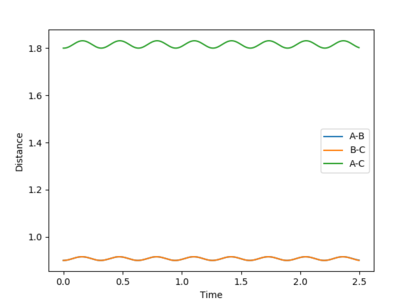
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

The best estimate that was reached was a r_ts = 0.907744 Å. This value was reached by using an initial estimate of .9 Å and the evaluating the distance versus time plot oscillation to find an estimate of the midpoint between the minimum and maximum of the oscillation, as the vibration would be about the true transition state position with an amplitude that was the distance the original estimate was away from the true value. This produced a more accurate estimate and this process was repeated 3 additional times.

A good way to find the TS point. But if you are at the exact TS point, what do you expect from the distance vibration? --Sw2711 (talk) 15:39, 31 May 2018 (BST)


Full Table	Zoomed on bond oscillation	Input r₁ = r₂
		0.90 Å
		0.907744 Å

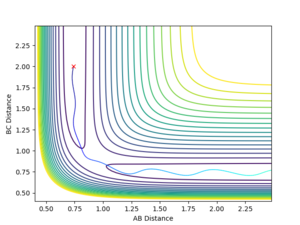
Comment on how the mep and the trajectory you just calculated differ.

The MEP plot that was calculated had no vibrational motion in the resulting bond while the inertial calculation did have this motion. This is because the inertial calculation takes into the inertial forces of H₂ and H₃ have as they constantly accelerate towards the ideal bond length. The MEP equation simply has the atoms fall together converging towards the ideal bond length.

I need some evidence to support your point.--Sw2711 (talk) 15:42, 31 May 2018 (BST)

Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive.


p₁	p₂	Total Energy	Reactivity	Plot + Description
-1.25	-2.5	-99.018	Reactive	In this case there is twice as much momentum in the free atom than the original bond. The overall energy is enough to overcome the transition state energy (ie activation energy). This case will serve as a basis for the following descriptions.
-1.5	-2	-100.456	Unreactive	The initial momenta are closer to being equal, but the total energy is lowered and does not exceed the activation energy. This means the activation energy is somewhere in the of -99 to -100.5. This leads to the colliding atom to remove absorb some of the vibration energy before being expelled at a higher velocity then when it first approached.
-1.5	-2.5	-98.956	Reactive	The total energy in this scenario is more positive than the first case and therefore has more energy than the activation energy. The resulting bond has more vibrational energy and the ejected atom has less momentum than the colliding atom original atom did.
-2.5	-5	-84.956	Unreactive	Initially the momenta are different by a factor of 2 as in the first example, but the total energy is much higher. While the total energy in the system is much more positive than the activation energy determined previously, it does not lead to a reaction. This can only be explained by the reaction path crossing the barrier an even number of times, 2 in this case.
-2.5	-5.2	-83.956	Reactive	Here there is also a barrier recrossing as in the previous scenario, but in this case there is an odd number of crossings, 3. Therefore it can be seen that at high total energies, above the activation energy, there are more complex effects than simply energy being more than the activation energy and the trajectory incidence on the transition saddle can have an effect on reactivity.

This part is good.--Sw2711 (talk) 15:44, 31 May 2018 (BST)

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

The main assumptions of Transition State Theory are that the atoms behave classical mechanics, that all intermediates are long lived, and that a reaction will cross the lowest energy surface saddle given it has enough energy to overcome the activation energy. The assumption that is relevant to the results that we have obtained is that it will cross the lowest saddle point given enough energy. This assumption is tested in rigor mathematically in our test and is proven to be not entirely true. We found that there are more complex effects, such as barrier recrossing, than simply is activation energy overcome. These effects can lead to a reaction that TST would predict to occur to not occur, leading to a lower reaction rate experimentally than TST would predict.

This part is good--Sw2711 (talk) 15:44, 31 May 2018 (BST)

F-H-H

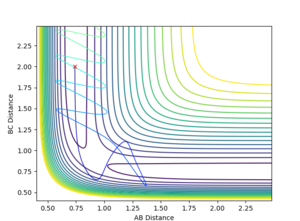
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?/Locate the approximate position of the transition state./Report the activation energy for both reactions.

I need some evidence how you find those reaction are endo/exo from the PES plot, how you find those activation energy and how you obtain your TS point.--Sw2711 (talk) 15:46, 31 May 2018 (BST)


Reaction	Energetics	Transition State Position	Activation Energy	Discussion of bond strength
F + H₂	Exothermic	F-H distance: 1.8106 Å H-H distance: 0.7453 Å	Ts Energy = -103.75 H-H bond = -104.02 Activation Energy = 0.27	The bond energy for F-H is less than that of H-H and therefore once the H₂ bond has been broken and the F-H bond has absorbed energy there is still a net release of energy. The energy of the reactants is greater than the energy of the products.
F-H + H	Endothermic	Same as above F-H distance: 1.8106 Å H-H distance: 0.7453 Å	Ts Energy = -103.75 F-H bond = -134.02 Activation Energy = 30.27	The bond energy of H-H is greater than F-H energy must be absorbed from vibrational or translational sources to break F-H and form H-H. The energy of the reactants is less than the energy of the products.

In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

This part is good--Sw2711 (talk) 15:47, 31 May 2018 (BST)

When energy is released it must be conserved and converted into another form of energy. The majority of released energy is usually converted into kinetic energy. In systems where the transition state is early translational energy is more effective at producing reactions, while late transitions states more effectively use vibrational energy. The kinetic energy released can be seen in the energy vs time graph below as there is a definite point where the kinetic energy increases and then starts to oscillate. This oscillation is due to the fact that the transition state for the F + H-H reaction is quite early leading to the majority of this produced kinetic energy to be vibrational. This is clearly seen in the momentum vs time graph as the A-B bond distance momentum vibrating largely in comparison with the B-C momenta of the released hydrogen. This effect can be seen and compared experimentally through calorimetry techniques. Translational motion is directly observed as temperature and therefore the increase in translational motion from a late transition state would most easily be seen in calorimetry as a large initial increase in temperature, and then a decrease as the kinetic energy was even distributed throughout all kinetic energy forms. In an early transition state the temperature, will also increase, but slower and without a peak as the temperature increase is not the primary effect of the reaction, but a secondary relaxation of the vibrational modes into other kinetic energy forms. Through the comparison of temperature vs time graphs a rough determination of position of the transition state can be estimated.


Energy vs Time	Momenta vs Time

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

The distribution of the kinetic energy available to overcome the transition state is important to determining the efficiency of the reaction. In cases where the energy is close to but always above the activation energy the trajectory of the reaction must incident the transition point with the correct orientation to produce a reaction. The location of the transitional barrier therefor determines which kinetic mode is more effective at producing a reaction.

In a late transition state, in relation to Hammond's postulate, the planar representation of of the barrier will be closer to parallel with the reactant's potential energy well. This means that the reactant molecule must contain some vibrational momentum to propel the reaction trajectory towards the barrier. Translational motion alone is not efficient in "turning the corner" into the products potential energy well. this is not to say it is not necessary. Vibrational energy also has the added determinant of time, as energy oscillates the trajectory as moving towards and away from the barrier. This means that in late transition state reactions, if vibrational energy is larger than the activation energy, it relies on the translational energy to determine if the overall system approaches the corner with the correct orientation to impact the barrier. However in an early transition state translational motion is most important in passing the barrier as pure translational motion is orthogonal to the barrier plane. Vibrational energy is still advantageous in "turning the corner", but is not the primary determinant of the efficiency.

Overall, the factor that determines the which mode is most important to the efficiency of a reaction is where the transition state occurs in the reaction path. A late transition state most effectively utilizes vibrational energy, while an early transition state more effectively utilizes translational motion.

Good explanation. But is it based on a theory or your experimental results? Do you agree or disagree with this statement?--Sw2711 (talk) 15:49, 31 May 2018 (BST)