MRD:LaraMetcalf

Molecular Reaction Dynamics Lab

EXERCISE 1: H + H2 system

A potential energy surface (PES) is a mathematical function which describes the electronic potential energy of a system as a function of the relative atomic positions in space and is widely used as a tool to carry out theoretical studies on molecular reaction dynamics .

Dynamics from the transition state region

The total gradient of the potential energy surface at a minimum and transition structure is equal to zero. The distinction between the two structures comes from the sign corresponding to their rate of change of gradient. The potential energy second derivative is positive for a minima and negative for a transition state . Which one? Along which direction? Je714 (talk) 17:36, 31 May 2017 (BST)

The transition structure linking the two minima is a maximum along the minima energy reaction pathway and thus is called a saddle point . This can be expressed mathematically by Taylor's Theorem :

If f_xxf_yy − f_x²_y < 0 at (a, b) then (a, b) is a saddle point.

If f_xx >0 and f_yy > 0 at (a,b) then (a,b) is a minimum point.

At the TS one of the partial 2nd derivatives will be >0 along one of the variables, and <0 along all the rest. Je714 (talk) 17:36, 31 May 2017 (BST)

Trajectories from r1 = r2: locating the transition state

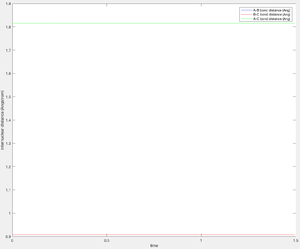
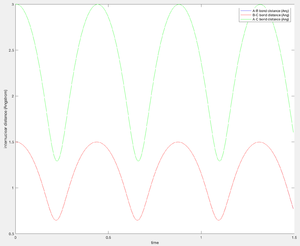
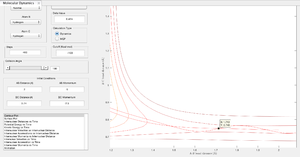
The best estimate of the transition state position r_ts is found to be equal to 0.90775 Å. The detection of the transition structure can be observed in an internuclear distances vs time plot. The transition state corresponds to where the gradient of the potential energy surface is zero, so it is expected that at rts the H atoms will be stationary - their internuclear separations will remain constant over time (fig 1). At a distance of 0.90775 Å the trajectory disappears (fig 2) confirming this to be a good approximation of the transition state position. Varying the interatomic distance away from the transition state position results in a trajectory that rolls back toward the reactants/products and thus a changing internuclear distance over time is observed (fig 3). Really? That's not what figure 3 is showing. Je714 (talk) 17:37, 31 May 2017 (BST)

Figure 1 - internuclear distance vs time plot at the transition state position.

Figure 2 - disappearance of the trajectory at the transition state position.

Figure 3 - internuclear distance vs time plot at r=1.5 A.

Figure 4 - surface plot displaying the trajectory at r=1.5 A.

Minimum Energy Path (MEP) and Dynamic Calculations

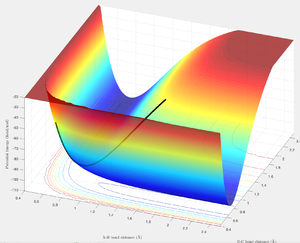
Both calculations produce trajectories that rolls from the reactants H1-H2 H3 in the direction of increasing r₁ towards H1 H2-H3 (r₁ = A-B) Upon energy minimisation the trajectory converges to the MEP . The MEP calculation generates the minimum energy trajectory thus is restricted to only one degree of freedom, the interatomic positions r₁ and r₂. The exchange between kinetic and potential energy (due to vibrations) does not occur as a result of the minimisation, and so the generated trajectory does not have an oscillative nature - the kinetic energy is fixed at zero. On the contrary the dynamics calculation does not involve such limitations allowing it to have more degrees of freedom generating an oscillating trajectory, signifying influence of a non-zero kinetic energy.

MEP Calculation Trajectory.

File:Lem215 dynamics.png

Dynamic Trajectory Calculation.

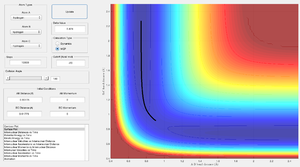
At large t (t): (3 decimal places)

r₁(1.485)= 5.247 Å

r₂(1.485) = 0.739 Å

p₁(1.45) = 2.481

p₂(1.45) = 1.260

Reverting the initial conditions so that r₁ = r_ts + 0.01 and r₂ = r_ts then the reaction would have a trajectory that rolls from H1 H2-H3 towards H1-H2 H3 in the direction of increasing r₂.

If the initial positions and final positions were swapped then the corresponding values for final momenta will have the opposite sign.

Reactive and unreactive trajectories

A series of initial condition were tested to determine whether or not they produce a reactive trajectory that starts from the reactants H_A-H_B and dissociated atom H_C to the molecular product H_B-H_C with dissociated atom H_A. Initial momenta p₁ of atom H_C approaching H_B before the transition state and final momenta p₂ of atom H_A moving away from the molecular product H_B-H_C

Initial Conditions

p1	p2	Reactivity
-1.25	-2.5	Reactive
-1.5	-2.0	Unreactive
-1.5	-2.5	Reactive
-2.5	-5	Unreactive
-2.5	-5.2	Reactive

Figure 5 - initial conditions p1=-1.25, p2=-2.5.

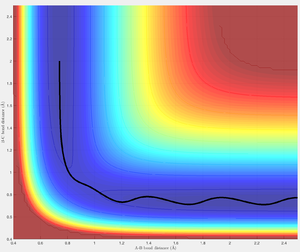
The first set of conditions generates a linear trajectory path from H_A-H_B H_C to the transition structure at approximately 0.908 Å. Before the collision r1 remains constant and r2 steadily decreases as H₃ approaches H₂. There is sufficient energy to overcome the activation energy barrier allowing the trajectory to roll towards the products. After the transition structure r₁ steadily increases as H_A moves away from H_B from the molecule formed H_B-H_C, the oscillating trajectory signifies the vibrational energy of the H_B-H_C bond.

Figure 6 - initial conditions p1=-1.5, p2=-2.0.

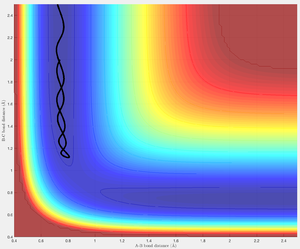
Increasing p1 and p2 (initial momenta), relative to the first set of conditions, results in an unreactive trajectory. Before the transition structure r₁ has a slight oscillation (vibrational energy of A-B) and r₂ steadily decreases as H_C approaches H_B. At r1=0.810 Å and r2=1.120 Å the trajectory bounces back toward the reactants. This suggests amount of energy available to the system is not sufficient to overcome the activation energy barrier - the reaction is unsuccessful. It is evident that the vibrational energy of H_A-H_B is retained upon the return of the system to the reactants.

Figure 7 - initial conditions p1=-1.5, p2=-2.5.

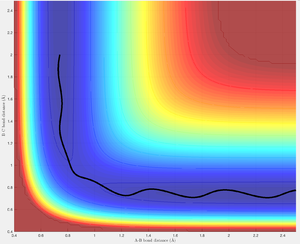
Increasing p₂ from -2.0 to -2.5 provides the energy required to overcome the barrier thus allowing the reaction to proceed. The trajectory rolls from the reactants to the products passing through the transition structure at 0.893 Å. Again the vibrational energy of the H_A-H_B then H_B-H_C bonds are observed before and after passing through the transition structure respectively.

Figure 8 - initial conditions p1=-2.5, p2=-5.0.

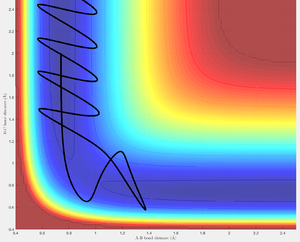
With the fourth set of initial momenta conditions the trajectory rolls from the reactants and passes through the transition structure illustrating an initial formation of the H_B-H_C bond. Soon after crossing the transition region the trajectory returns to the reactants - this is an example barrier re-crossing. The trajectory bounces several times within a small region about transition state position before returning back to the reactants.

Figure 9 - initial conditions p1=-2.5, p2=-5.2.

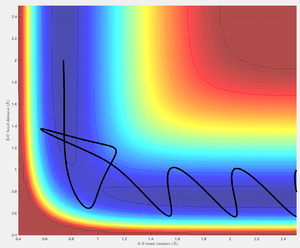
The trajectory approaches the transition structure along the direction of decreasing r₂ at a constant r₁. Again the trajectory displays barrier re-crossing before eventually bouncing across the barrier toward the product H_B-H_C and dissociated atom H_A.

The final two sets of initial momenta have relatively large p₂ values. Both systems have significant translational kinetic energy as H atom A moves away from the formed molecule H_B-H_C. At high kinetic translational energies of atoms/molecules it becomes increasingly difficult to justify the differences in the reactivity of the generated trajectories. This suggests the application of Transition State Theory is unsuitable for dynamic molecular systems of this type - this method is limiting.

Transition State Theory

The transition state is the known as the 'critical configuration' that corresponds to the highest point on a minimum energy reaction pathway on a potential energy surface . If the system is able to reach the critical geometry then a successful reaction is highly probable. The transition structure is a stationary point thus is identified as the saddle point, with associated reaction coordinates, on a potential energy surface. The transition state theory is a cumulative a series of assumptions used to approximate the equilibrium rate constants for thermally driven molecular reactions . The TST stemmed from thermodynamic, kinetic-theory and statistical mechanic treatments .

Development of the Transition State Theory

The thermodynamic treatment stems from the Van't Hoff equation which relates the change in the equilibrium constant (k_eq) to a given change in temperature (T) for a given enthalpy change (delta H):

$\ln K_{\mathrm{e}\mathrm{q}}=-\frac{\mathrm{\Delta }{H}^{\ominus }}{RT}+\frac{\mathrm{\Delta }{S}^{\ominus }}{R}.$.

The kinetic-theory explains the temperature dependence of reaction rates as a function of collision frequency and the statistical mechanical treatment focuses on equilibrium reaction rates in terms of the motion of molecules and statistical distribution of molecular speeds - initially modelled by Maxwell and Boltzmann.

Main Features and Assumptions of the Transition State Theory

(1) Rates can be calculated by focusing on the "activated complex" - what happens before the transition state is reached are not important if one rate dominates the overall rate of reaction.

(2) The activated complex is formed in 'quasi-equilibrium' i.e. the complex is in equilibrium with the reactants and products passing through - the concentrations of reactants and products can be determined by changing the concentration of one species e.g. removing the products.

(3) Motion of the system is treated as 'free translational motion' - expressed by kinetic-theory.

Using the Transition State Theory to Determine Reactivity

The TST ignores the dynamical recrossings that can lead back to the reactants (also known as tunneling) so this calculation tends to overestimate the rates within the classical mechanic framework . For a successful reaction the molecular system must have sufficient energy to overcome the activation energy barrier and thus generate a reactive trajectory. The Arrhenius equation relates the activate energy to the reaction rate for a particular reaction scheme, k=Ae^(-Ea/RT) . The relationship shows how a small activation energy barrier will correspond to a larger reaction rate constant - the reaction will go faster. It is likely that the experimental activation energy barrier will be larger than the calculated value thus TST will likely overestimate the rate relative the the experimental rate for a given reaction.

Good job looking up information. Just a small point -- the statistical mechanical treatment does not really hold here, since we are not looking at an ensemble of particles, just at a simple triatomic collision in isolation. The biggest point to be made here, was the recrossing limitation, and how that overestimates the rates when compared to experiment. Because that's the most relevant limitation that you observe in this lab. Je714 (talk) 17:40, 31 May 2017 (BST)

EXERCISE 2: F - H - H system

Reaction Energetics

The F + H₂ reaction is exothermic. An exothermic reaction is defined as the reaction path from a higher (reactants) to lower total potential energy (products) . The trajectory shows the approach of F to H₂ from infinite separation (as it is dissociated): as A-B separation decreases the potential energy decreases to a minimum indicating the H-F bond formation and H-H bond dissociation is an exothermic process.

Figure 10 - Surface Plot Trajectory from F + H₂ to F-H + H.

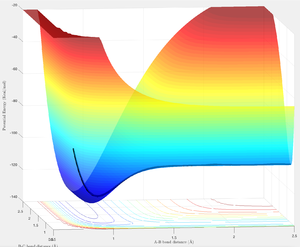
By definition the reverse of an exothermic reaction is endothermic , this is indicated by the trajectory generate by the H-F + H reaction. H-F bond breaking and H-H bond forming is an endothermic and enthalpically unfavourable process. The reactants have a lower total potential energy than the products.

Figure 11 - Surface Plot Trajectory from F-H + H to F + H₂

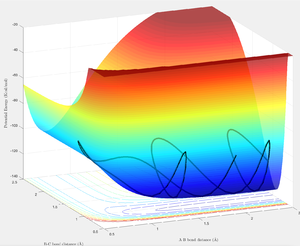
The H-F bond formation has a more negative (exothermic) reaction enthalpy indicating H-F to have a stronger bond than H₂.

Location of Transition State and Determination of the Activation Energies

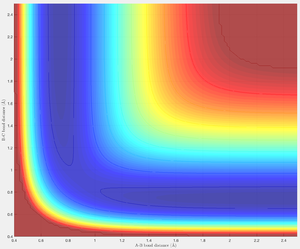
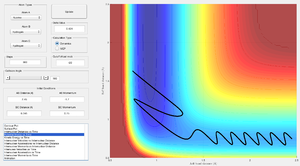
Rates of reactions are controlled by the free energy of the transition state and Hammond postulated that the structure of a given transition state will more closely resemble that of the reactants or products depending on which is closer in energy . He concluded that for an exothermic reaction the transition state will be more structurally similar to the reactants i.e. the interconversion between the reactants and transition state will involve only a small reorganization of molecular structure. And conversely for an endothermic reaction the transition state will be more structurally related to the products. The transition structure is expected to be closer in energy and structure to the reactants - longer A-B and shorter B-C distance so point of intersection further right in the saddle region was selected to determine the location (see figure 12) and energy of the transition state.

Approximate location of the transition state (3 dp):

A-B (F-H) = 1.713 Å

B-C (H-H) = 0.748 Å

Figure 12 - Locating the transition state for a F-H-H system.

Activation energies (2 dp):

Figure 13 - Determination of the absolute energy for products (F-H + H).

Energy of the reactants (F + H2) = -103.80 kcal/mol

Energy of the products (F-H + H) = -134.00 kcal/mol

Energy of the transition structure = -96.47 kcal/mol

Activation energy for formation of HF + H = +7.33 kcal/mol (=-96.47--103.80)

Activation energy for formation of F + H2 = +37.53 kcal/mol (=-96.47--134.00)

How did you get the Eas? They're not very accurate Je714 (talk) 17:41, 31 May 2017 (BST)

Reaction Dynamics

Mechanism of Release of Reactant Energy

Figure 14 - Reactive Trajectory for F + H₂.

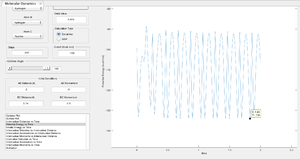
The amplitude of the oscillating trajectory reflects the magnitude of the defined initial momenta values. The reactants produce an oscillation of smaller amplitude than the products as p1 (H-H) < p2 (F-H). The trajectories before and after the transition state however differ by the period of the generated oscillations - this indicates differences in the translational kinetic energy in the reactants and products. It has been discussed previously that the molecular product H-F has a stronger bond than H-H so it is expected to ‘see’ a greater translational kinetic energy in the products than the reactants. This is displayed by the trajectory, the oscillation period for the product H-F (A-B) is larger than that of the reactant H-H (B-C). As a result of the conservation of energy, the total energy of the system must remain constant . Therefore the product state should have a lower potential energy than the reactants to balance the total energy (kinetic and potential) of the system so that it remains constant, suggesting the reaction to be exothermic - earlier concluded to be the case as for the reaction for F + H₂. This could be confirmed by different spectroscopic methods such as calorimetry and IR/Raman spectroscopy.

Heat-flow calorimetry is commonly used to thermally monitor reactions and thus determine whether a reaction is exothermic or endothermic. The heat transfer under e.g. constant pressure is monitored as the reaction proceeds and consequently the enthalpy change can be determined. Thermodynamically ΔH=q_p at constant pressure (where q_p is the heat flow at constant pressure), otherwise known as Hess's Law . Exothermic reactions release heat thus if exothermic the calculated value for the enthalpy change will be negative in sign (visa versa for endothermic reactions).

IR/Raman spectroscopy is used to determine the vibrational states of molecules/matter. If the reactants possess less translational kinetic energy and thus vibrational energy then the IR spectra for the reactants should display lower intensity peaks relative to the peaks in the IR spectra of the products.

Good experimental suggestions. Je714 (talk) 17:41, 31 May 2017 (BST)

Polanyi's empirical rules

Polanyi's empirical rules focus on the importance of the transition state location in enhancing reactivity for activated reactions . This model has enabled the prediction of the relative efficacy of vibrational and translational excitations in promoting different molecular dynamic reactions.

Polanyi's rules state that vibrational energy is more efficient at promoting late transition states (endothermic reactions according to Hammond Postulate ) than translational energy. And conversely translational kinetic energy is more efficient at promoting 'early' transition states (exothermic reactions).

The reaction from H + H-F provides an illustration of these rules. This reaction is endothermic, thus is an example of a late-barrier reaction - the transition state is closer to the products in energy and structure according to Hammond's Postulate . According to the Polanyi's Empirical Rules the reactivity should be enhanced more efficiently by high vibrational energy (and low kinetic energy). When initial conditions were chosen so that the reactant H-H had high vibrational energy (high p_HH) and low translational kinetic energy (small p_HF) a kinetically driven trajectory was generated.

Not all systems obey Polanyi's Rules as a result of their empirical nature (experimentally determined). As the rules are experimentally determined they effectively relate to the average behaviour of a reacting system . The reaction H₂ + F is an example where the calculated trajectory deviates from Polanyi's predictions. This reaction is exothermic so according to Polanyi's rules it is expected that high translational kinetic energy would promote the early transition state and thus enhance the reactivity. However for the reactive trajectory to reach completion a higher initial momenta for H-H (p_HH) than initial translational kinetic energy (p_HF) was required. This may be due to the errors in the computational calculation of the reaction trajectory thus does not accurately portray was would be observed experimentally.

Missing some examples here with your trajectories. Je714 (talk) 17:42, 31 May 2017 (BST)

References: