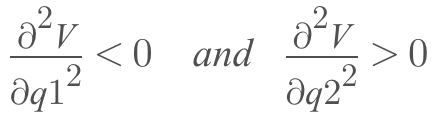MRD:LE1517

Exercise 1: H + H2 system

Dynamics from the transition state region

On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?

A transition state is the point where the rate of change of potential with respect to intermolecular distance reaches zero. The transition state can be identified where a saddle point (a point where both the differential of potential with respect to AB and BC are both equal to 0) is present on surface plot. A local minimum will only equal 0 as the differential of potential with respect to AB or BC but not both. Differential of surface plot provides a function for the trajectory of the reactants. This function can be differentiated at its maximum point to find the minimum value of potential energy since this would be the second differential of the surface plot which, providing a positive value, would separate it from any other point on the plot where the first differential is equal to 0.

There is some confusion here:

• 'rate' is usually reserved to time derivatives

• the saddle point is not just defined by the first derivatives being zero

• As is the case for the saddle point, the first derivatives have to be zero for the minimum, too.

• the last sentence is barely understandable.

Fdp18 (talk) 19:50, 20 May 2019 (BST)

Your equations have the potential to be correct, depending on how you define the quantities in them. Those definitions, however, are not given. Fdp18 (talk) 20:02, 20 May 2019 (BST)

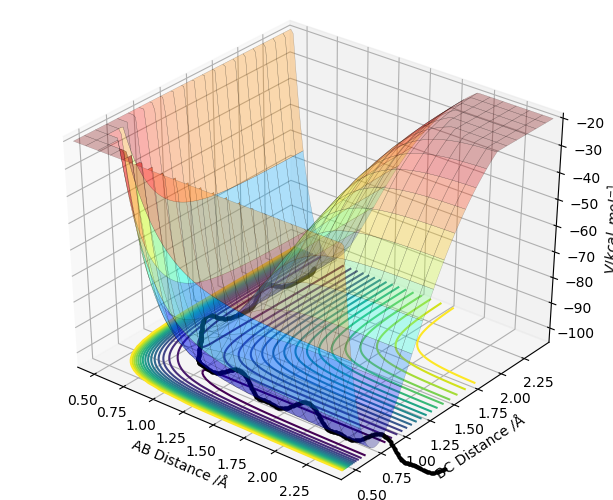
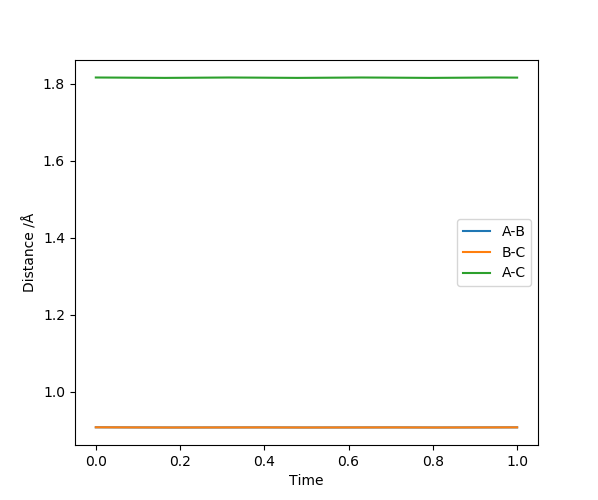
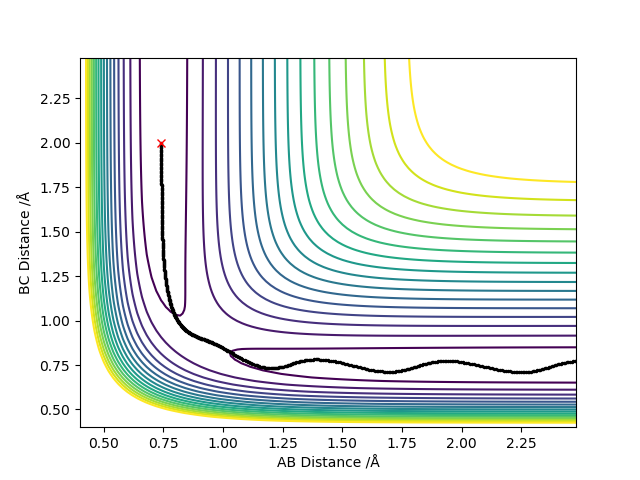
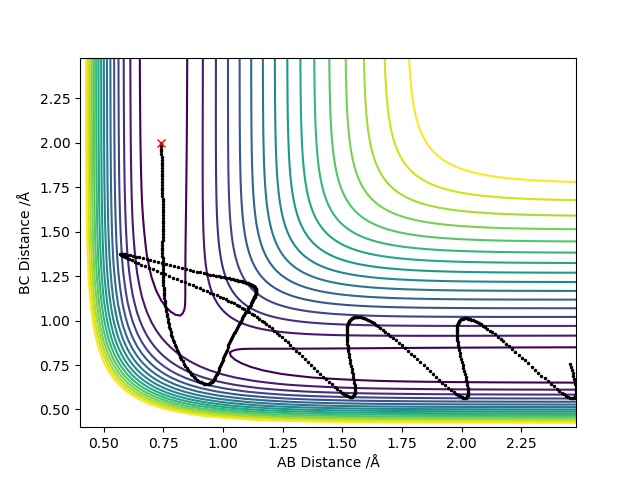
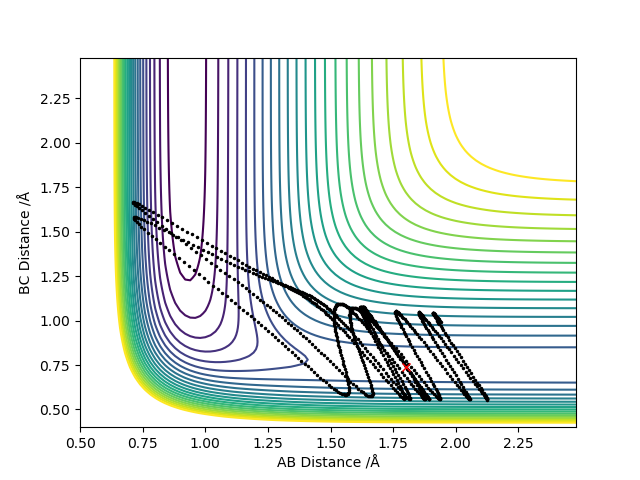
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

Potential Energy of Surface

Where r1 = r2 = 0.908 Å

As the transition state is reached, r₁ and r₂ distances become equal since the trajectory will oscillate about this most stable point. The outer two hydrogen atoms vibrate symmetrically and the estimated transition state position is where r₁ = r₂ = 0.908 Å, where p₁ = p₂ = 0. In the image above, the transition state is reached where oscillation is reduced to a minimum since this is where energy is at its lowest point. The transition state is neither the most stable point, nor is is the point of lowest energy. You should carefully revise TST. Fdp18 (talk) 19:52, 20 May 2019 (BST)

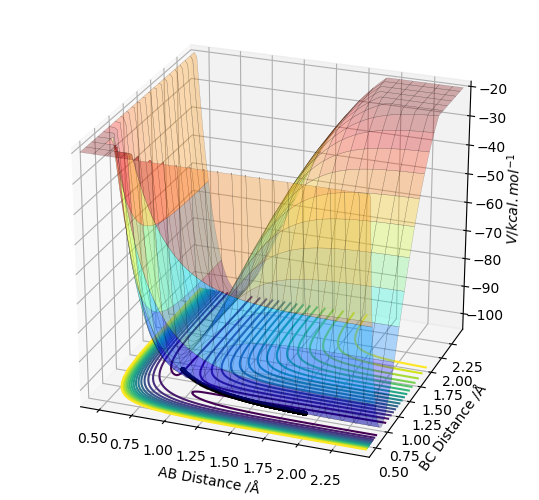
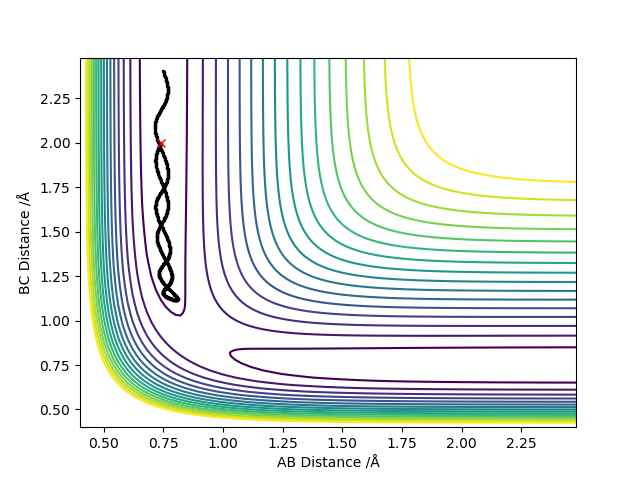
Comment on how the mep and the trajectory you just calculated differ.

Calculating the trajectory using the dynamic mode provides a much longer trajectory which goes along the surface floor as opposed to the MEP calculation which provides a much shorter trajectory which is a result of setting the velocity to zero in each step whereas the dynamic calculation does not do this and so the atoms will have a larger speed at any given point than the atoms in the MEP calculation. The dyanmics calculation therefore provides a more realistic view of the motion of the particles of the system sine the particles have momenta and are not going to lose all momentum unless met with the correct force to do so. This is represented through the oscillatory nature of the dynamic calculations.

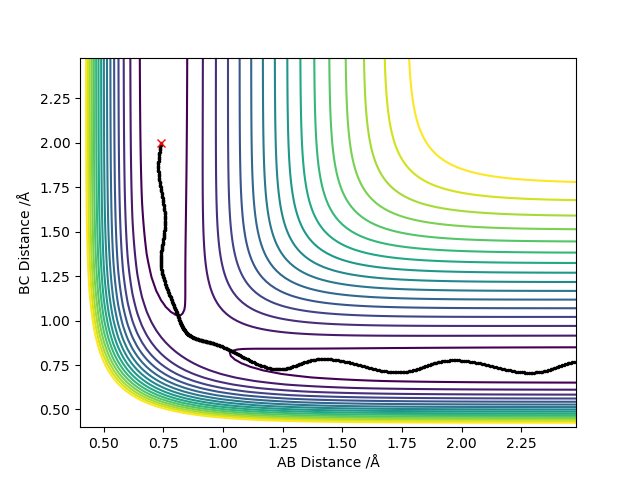
As expected, when AB and BC values were swapped, their respective positions on the graph swapped also due to the equivalent nature of the atoms being considered.

Alternating values of AB and BC for Internuclear Distances vs Time

Alternating values of AB and BC for Internuclear Distances vs Time

Alternating values of AB and BC for Momenta vs Time

Alternating values of AB and BC for Momenta vs Time

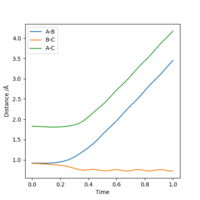
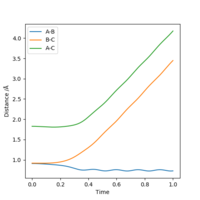
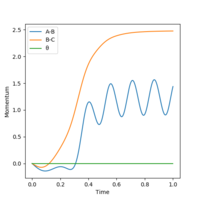
Reactive and unreactive trajectories

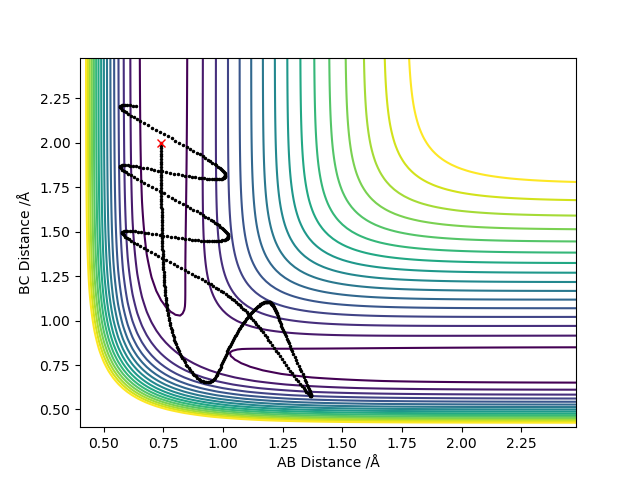
Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?

p1	p2	Etot (kcal mol-1)	Reactive?	Description of the dynamics	Illustration of the trajectory
-1.25	-2.5	-99.0	Yes	H+ ion approaches H2 and is able to withdraw a hydrogen atom, new H+ ion now has momentum in opposite direction to initial motion
-1.5	-2.0	-100.45	No	H+ ion approaches but comes to a momentary stationary point away from the H2 molecule and so is unable to react and withdraw a H atom
-1.5	-2.5	-98.96	Yes	H+ ion approaches H2 and just as the H2 molecule is about to reverse its momentum, a H atom is withdrawn, seemingly very close to the activation energy barrier
-2.5	-5.0	-84.96	No	H+ ion approaches very rapidly and withdraws a H atom but the new H2 molecule vibrates rapidly and so the newly formed H+ ion is able to recapture the withdrawn H atom to reform the original H2 molecule
-2.5	-5.2	-83.42	Yes	H+ ion approaches very rapidly and withdraws a H atom but the new H2 molecule vibrates rapidly and so the newly formed H+ ion is able to recapture the withdrawn H atom momentarily and it then returns to the initial H+ ion to form a H2 molecule

It can be concluded that the momentum of the particles determine whether or not a reaction will take place and that total energy does not play a part in this seeing as systems with higher total energies failed to react where as those with less energy were able to.

That 'the total energy does not play a part in this' is a potentially controversial statement. Consider rephrasing it. Fdp18 (talk) 19:56, 20 May 2019 (BST)

Assumptions of Transition State Theory

Transition state theory looks to explain chemical reaction rates through the assumption of a quasi-equilibrium between the reactants and so called activated transition state complexes. The rate at which the final state is reached is controlled by the number of activated complexes are formed and how fast those complexes form into the final state. Given that having higher energy and therefore higher energy activated complexes does not necessarily lead to reaction, it is highly likely that Transition state theory overestimates reaction rate values in comparison to experimental data.

Exercise 2: F - H - H system

PES inspection

By inspecting the potential energy surfaces, classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

The potential shows that F + H₂ → H + HF is an exothermic reaction since the products are of a lower energy than the reactants. As a result of this, the reverse reaction must be endothermic. The reverse reaction could already be assumed to be endothermic given the strong ionic bonding character of H-F, due to the large difference in electronegativities, making it more likely to have a higher bond energy than that of H-H.

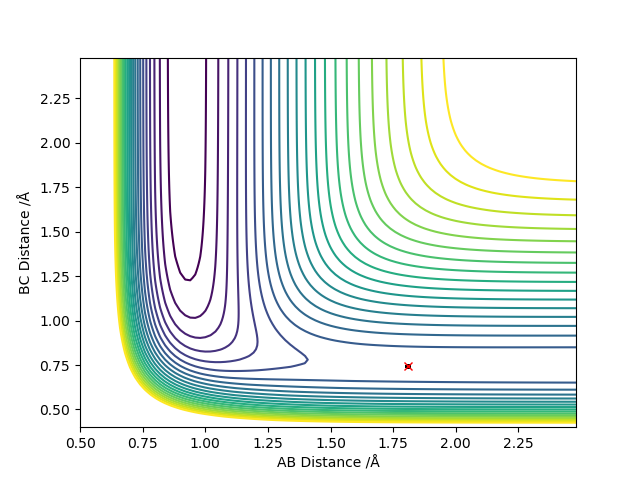
Locate the approximate position of the transition state

The transition state was located by setting the momentums of each component to zero and manipulating the AB and BC distances to find an optimum value of 1.808 Å and 0.745 Å for AB and BC respectively where F-H is AB and H-H is BC

Report the activation energy for both reactions

Transition state: -103.75 kcal mol^-1

F + H₂ → H + HF:

Reactants: -104.02 kcal mol^-1

Products: -133.71 kcal mol^-1

Activation energy for exothermic reaction: -29.96 kcal mol^-1

Activation energy for exothermic reaction: 0.27 kcal mol^-1

Reaction dynamics

Mechanism of release of the reaction energy and experimental confirmation

Energy from the reaction is most likely released in the forms of vibrational and translational energy. The animations show that when a collision occurs, translational energy is converted into vibrational energy within the newly formed compound. Vibrational energy can be measured through a range of spectroscopic techniques, namely UV and IR spectroscopy. Given that the forward reaction is exothermic, energy will be given out to the surroundings which means the initial translational energy could be measured through the use of a calorimeter.

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state

pHH	Observation on vibrations	Reactive?
-3	Extremely strong	Yes
-2.95	Extremely strong	No
-2.9	Extremely strong	Yes
-2.85	Quite strong	No
-2.8	Quite strong	No
-2.6	Strong	No
-2.3	Strong	Yes
-2	Medium	Yes
-1.5	Medium	Yes
-1	Weak	No
-0.5	Quite weak	Yes
0	Extremely weak	Yes
0.5	Weak	Yes
1	Medium	No
1.5	Medium	No
2	Strong	Yes
2.3	Strong	No
2.6	Quite strong	No
2.8	Quite strong	No
2.85	Extremely strong	Yes
2.9	Extremely strong	No
2.95	Extremely strong	No
3	Extremely strong	No

The table above shows how reactivity varies with changing momentum of the H₂ molecule where p_FH= -0.5, r_HH= 0.74 Å and r_FH= 2.4 Å. The table shows no clear trend as to how momentum affects the reactivity since a wide variety of momentums provided successful reactions.

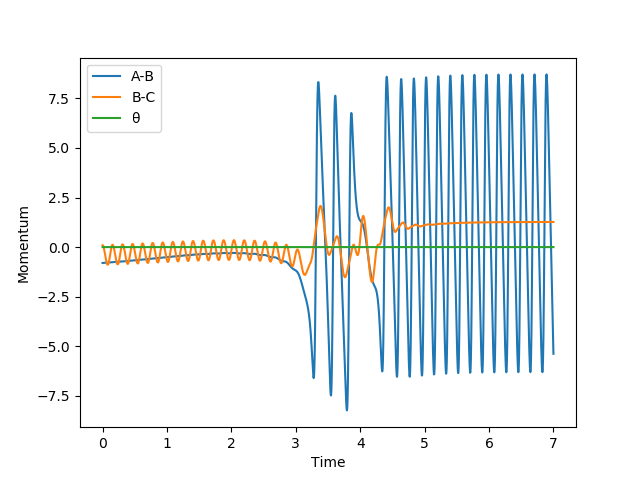
A possible reactive trajectory was found with both initial positions remaining and where p_FH= -0.8 and p_HH= 0.1.

Another reactive trajectory was found, in this case for H + HF, where p_FH= -0.01, p_HH= -10, r_FH= 0.87 Å and r_HH= 2 Å.

Polanyi's Rules

Polanyi set out rules explaining how early and late transition states would be more greatly affected by translational and vibrational energies, respectively. Wording: 'more greatly affected' VS 'more easily overcome' - you mean the right thing, but it is not quite correct. Fdp18 (talk) 20:00, 20 May 2019 (BST)

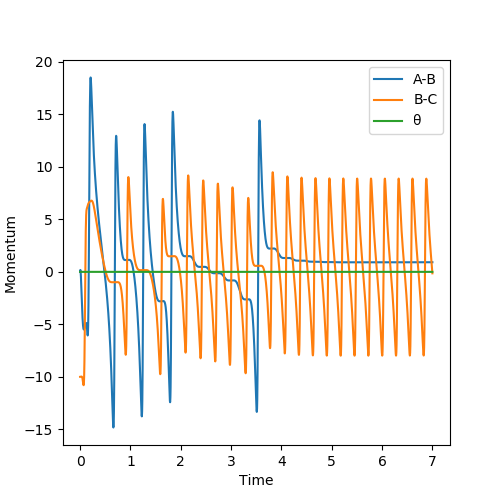
Since the reaction F + H2 → H + HF is an exothermic reaction, translational energy should have a larger effect on the efficiency of the reaction as it has an early transition state whereas the reverse reaction would have is efficiency determined more by the vibrational energy it possesses due to its late transition state. The translational energy of the forward reaction is represented through the momentum of the fluorine atom and its vibrational energy through the momentum of the H2 molecule. The theory predicts therefore, that a higher vibrational energy will not be as efficient and this is true as the H-H momentum from the plot below can be raised from -1 to -5, leading to no reaction. However the table above shows that the system can disobey Polanyi's rules given the right initial conditions.