MRD:KGW15

EXERCISE 1: H + H₂ system

Q1

At a transition structure, both ∂V(r_A-B)/∂r_A-B and ∂V(r_B-C)/∂r_B-C are 0. The same applies to the minima. The two can be distinguished with the second derivatives: at the transition state, ∂V(r_A-B)/∂r_A-B (where A is the leaving atom) is positive while ∂V(r_B-C)/∂r_B-C is negative.

(Your derivatives and second derivatives are the same here. The derivative measures the potential for the whole system, not just one coordinate. Finally, the coordinates at the TS are not the same as R_AB and R_BC when determining what the curvature is. If you recall the diagram of the MEP, the reaction coordinate changes direction and becomes 45º - a linear combination of R_AB and R_BC. Tam10 (talk) 16:14, 6 June 2017 (BST))

Q2

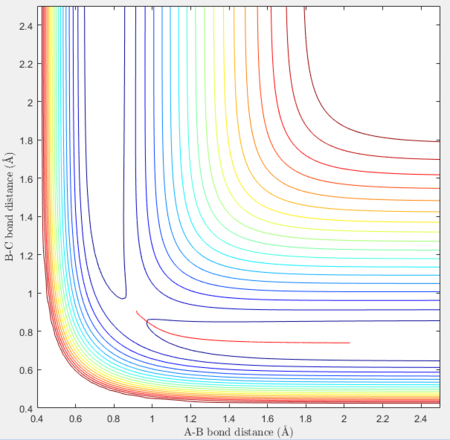
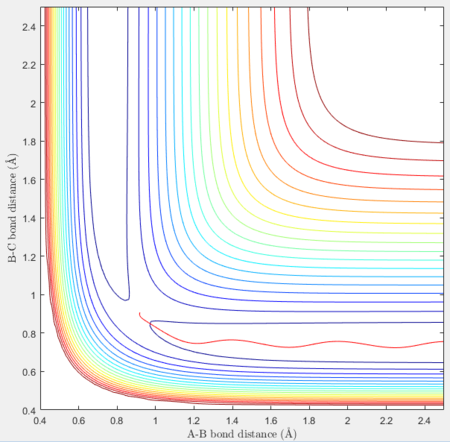
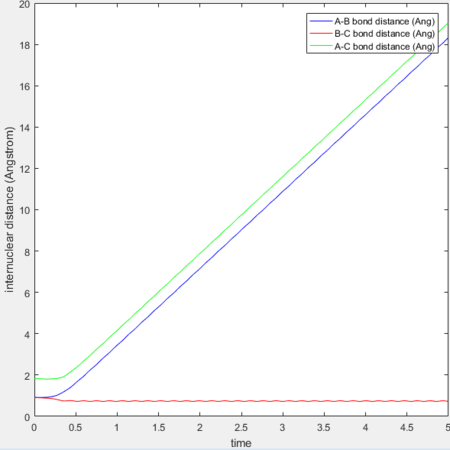
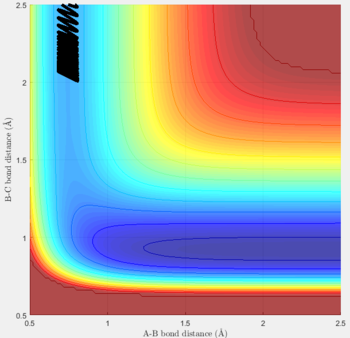
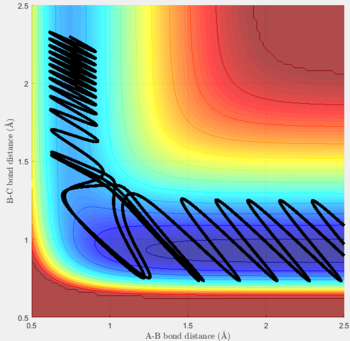
Transition state position (rts): 0.90775Å

It was estimated from the intersection point in the original "bond distances vs time" graph, then refined by trial and error. The constant distance can be implied as the transition state position because with particles with zero momenta sitting at the saddle point would be motionless and stay at that position.

Figure 1: Constant intermolecular distances at transition state

Q3

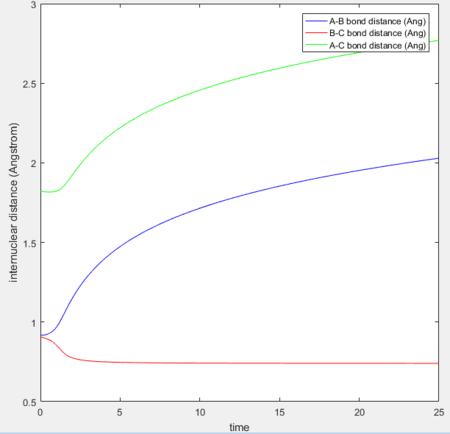
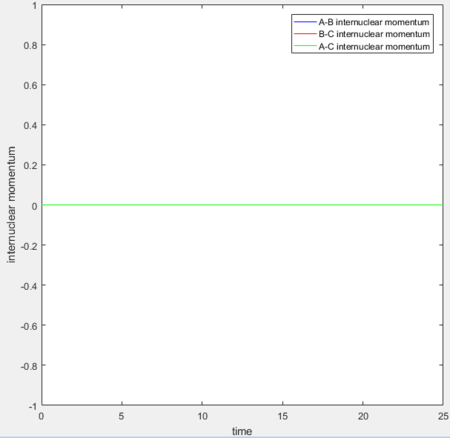
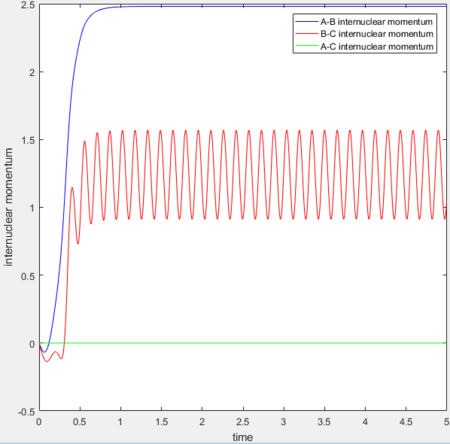
MEP vs 'relistic' trajectory: Molecular vibration is taken into consideration for Dynamics calculation but not in MEP. It is due to the fact that MEP assumes the atoms have zero velocity and thus zero momentum.

Setting r_AB= r_ts+0.01, r_BC = r_ts and the momenta p_AB = p_BC = 0,

for MEP: the final value of the position r_AB(t) = 2.029Å, r_BC(t) = 0.741Å and the average momenta p_AB(t) = 0 and p_BC(t) = 0 at large t.

for Dynamics: the final value of the position r_AB(t) tends to infinity, r_BC(t) = 0.740Å and the average momenta p_AB(t) = 2.481 and p_BC(t) = 1.241 at large t.

MEP	Figure 2: Contour plot using MEP	Figure 3: Distance vs time plot using MEP	Figure 4: Momentum vs time plot using MEP
Dynamics Calculation	Figure 2: Contour plot using dynamics approach	Figure 3: Distance vs time plot using dynamics approach	Figure 4: Momentum vs time plot using dynamics approach

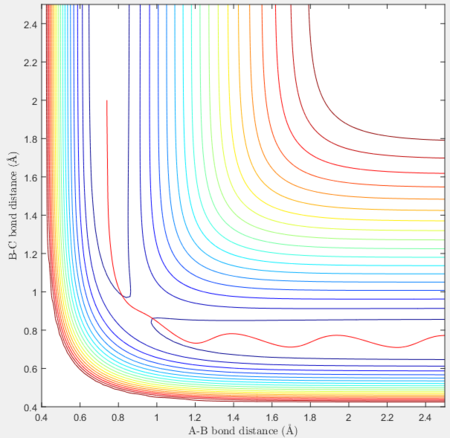
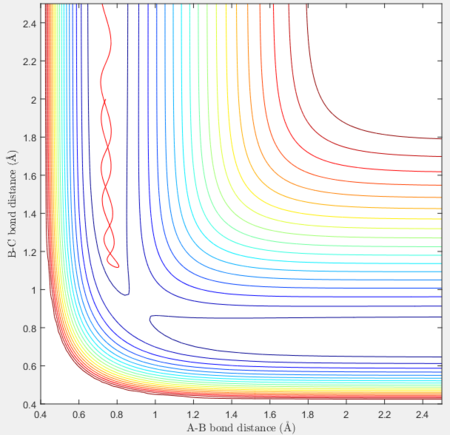
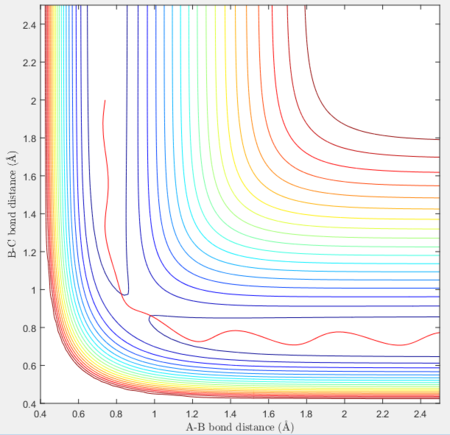
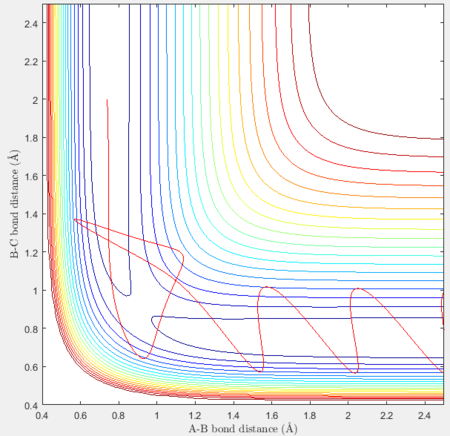
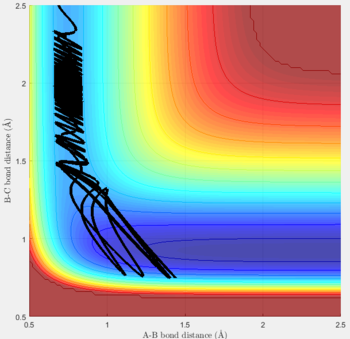
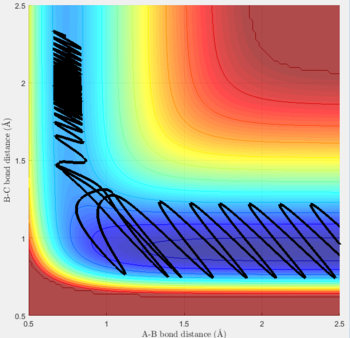
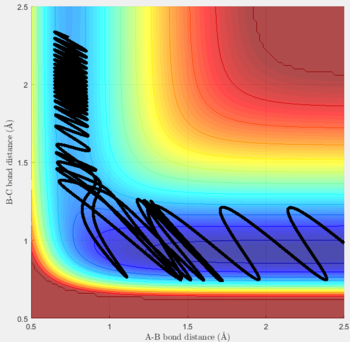
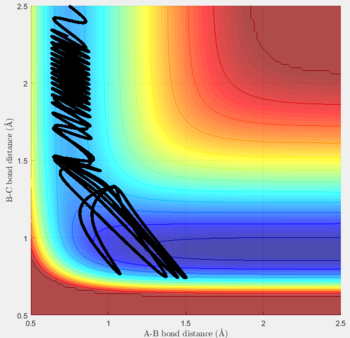
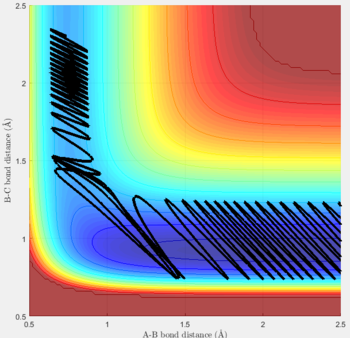
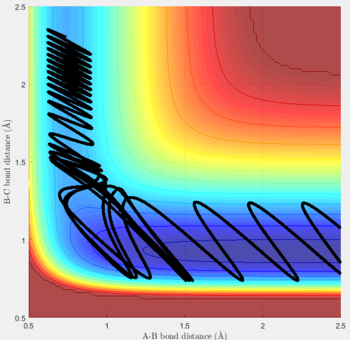
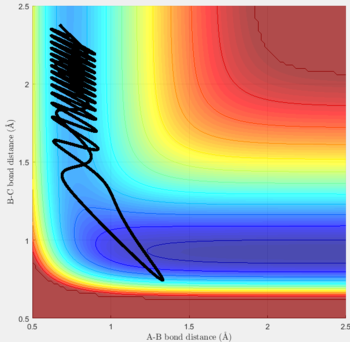
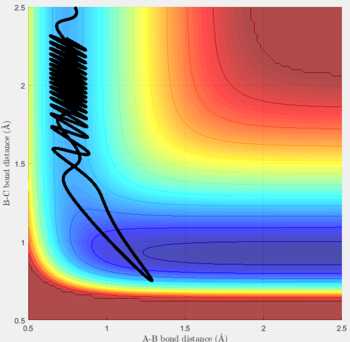
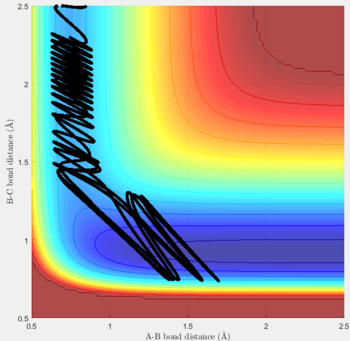
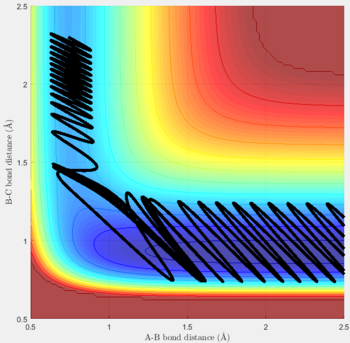
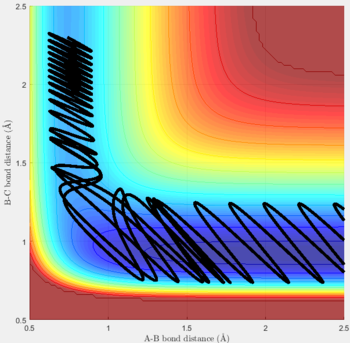
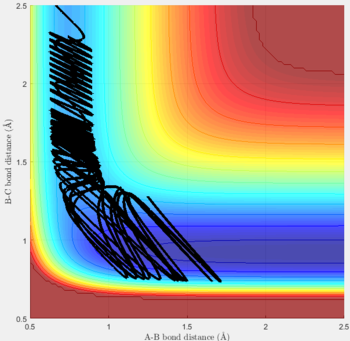
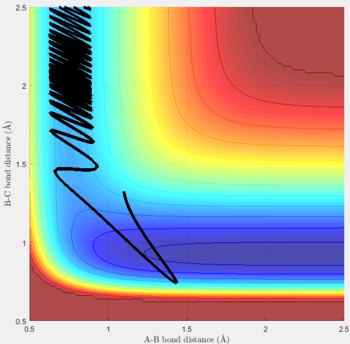
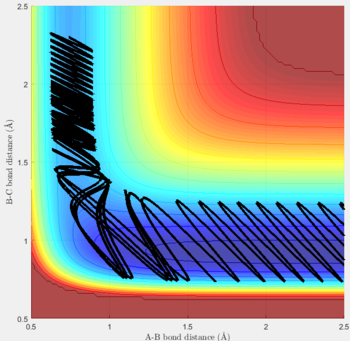
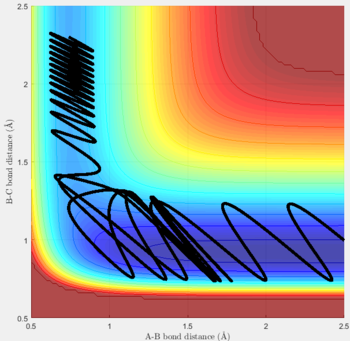
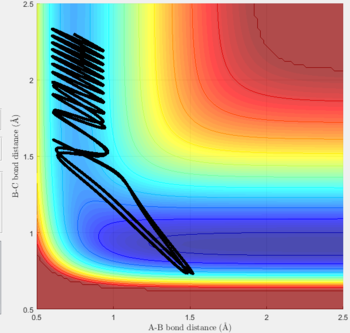
Reactive and unreactive trajectories

For the initial positions r₁ = 0.74 and r₂= 2.0, trajectories with the following momenta combination were run:

p1	p2	Trajectory	Description
-1.25	-2.5	Figure 5: Contour plot, p1=-1.25 and p1=-2.5	Reactive, the trajectory passed through the transition barrier, meaning the hydrogen C passed through the activation barrier successfully.
-1.5	-2.0	Figure 6: Contour plot, p1=-1.5 and p1=-2.0	Unreactive, hydrogen C was launched away as A-B continued vibrating as a molecule.
-1.5	-2.5	Figure 7: Contour plot, p1=-1.5 and p1=-2.5	Reactive, the trajectory passed through the transition barrier, meaning the hydrogen C passed through the activation barrier successfully.
-2.5	-5.0	Figure 8: Contour plot, p1=-2.5 and p1=-5.0	Unreactive, hydrogen C passed through the activation barrier, disrupting A-B molecule and bonded with B momentarily before it was launched away while A-B reformed as a molecule, vibrating with a large amplitude.
-2.5	-5.2	Figure 9: Contour plot, p1=-2.5 and p1=-5.2	Reactive, hydrogen C passed through the activation barrier and bonded with B with large vibrational amplitude.

Transition State Theory

Transition state theory (TST) assumes that once the reactants reach the transition state, it will proceed towards the products. From the calculations made above, TST fell short in some cases where it did not predict systems being able to revert to the reactants after reaching transition state. Therefore predicted reaction rate values will be higher than experimental values since it does not take into account the rate of backwards reaction of transition states.

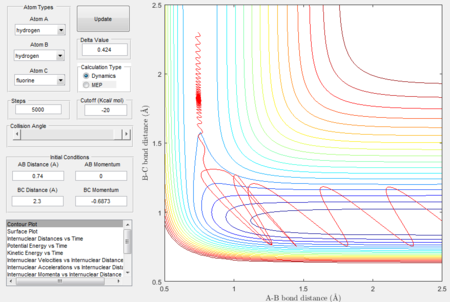
EXERCISE 2: F - H - H system

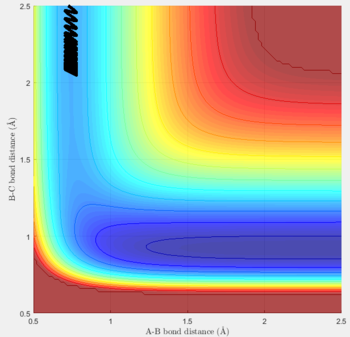
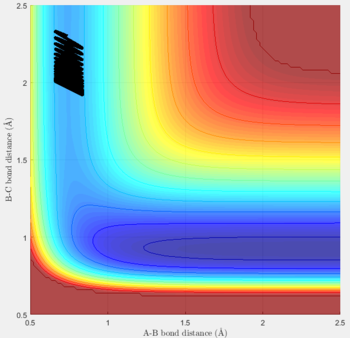
PES inspection

The F + H₂ reaction is exothermic. It can be seen on the PES that H-F has a lower potential energy than H-H. Since H + HF is the reverse of the F + H₂ reaction, it is endothermic. From this, we can interpret that H-F bond strength is higher than that of H-H.

Figure 10: Contour plot, F + H₂, the deeper blue colour indicates a steeper potential energy

Transition state approximation

Since the system is not symmetric, the H-F and H-H bond length is not the same at the transition state. Moreover, it is difficult to extract information of the transition state from the trajectory calculated above.

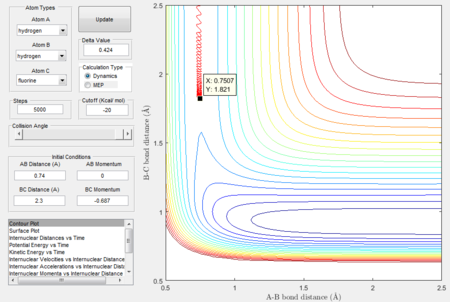
An approximation can be made initially by a method similar to bisection: two initial momenta, p₁ and p₂ are searched such that the fluorine with p₁ will not cross the activation barrier, whereas the one with p₂ will have the sufficient energy to just cross the barrier. Thus the momentum p_x with the exact amount of energy to lie on top of the activation barrier will be between (p₁, p₂). The position of the atom can be found accordingly:

Figure 11: p1 = -0.687, H-F = 1.821Å and H-H = 0.7507Å will be a gross approximation to the transition bond lengths

Figure 12: p2 = -0.6873

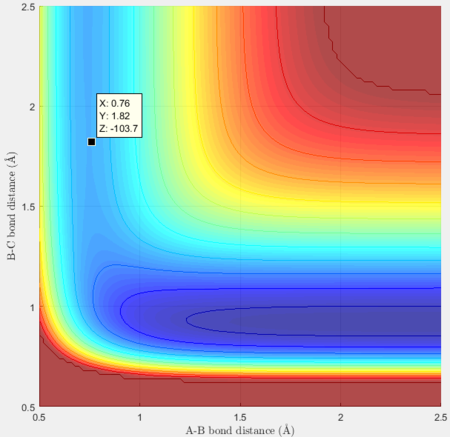
MEP calculations are carried out to verify the approximation:

Figure 13: MEP with H-F = 1.821Å and H-H = 0.7507Å

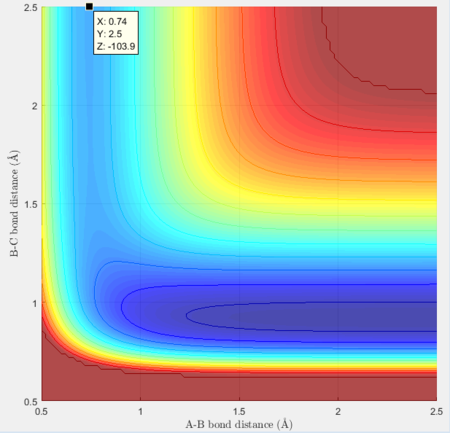
Thus the approximate transition state is at H-F = 1.821Å and H-H = 0.7507Å

Activation energy for both reactions

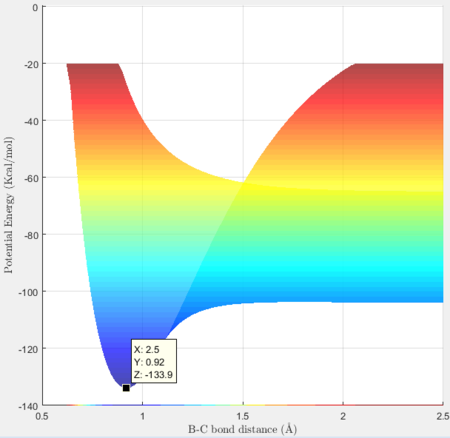
The activation energy for a reaction is the difference between the potential energy of the transition state and that of the reactants.

Ideally, the potential energy for the reactants should be measured where the reactants are separated infinitely. However, due to the limitations of the model, the maximum separation can only be 2.5Å, which potentially introduces a large error.

Activation energy for F + H₂= -103.7 + 103.9 = 0.2 kcal/mol, which is largely different to literature value of 1.68 kcal/mol^[1]

Activation energy for H + HF = -103.7 + 133.9 = 30.2 kcal/mol

Figure 14: Potential energy of F-H

Figure 15: Potential energy of transition state

Figure 16: Potential energy of H-H

Reaction dynamics

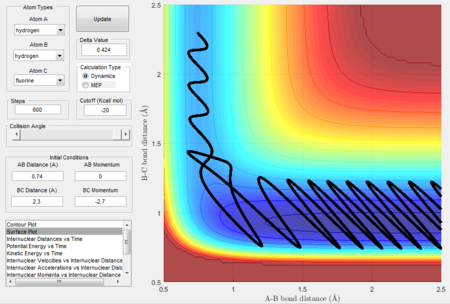
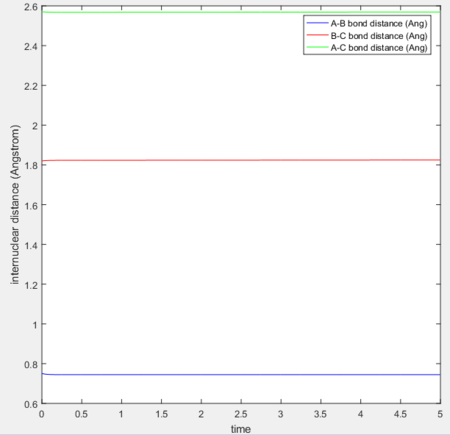
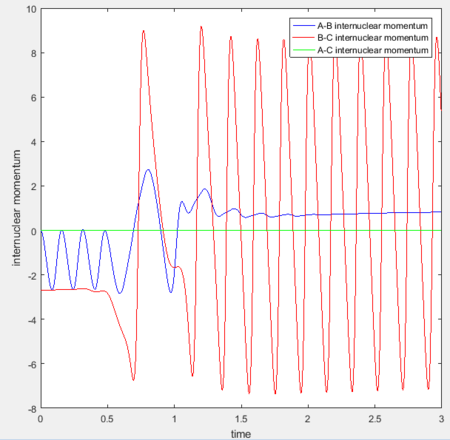
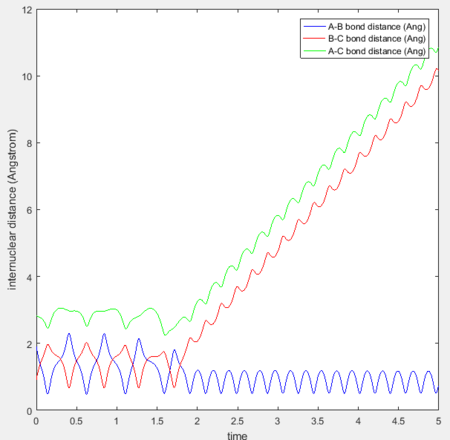
Initial conditions were set as previously shown in Fig 10: H-H distance = 0.74Å, H-F distance = 2.3Å, H-H momentum = 0, H-F momentum = -2.7. Simulation results are as shown:

Figure 17: Momentum over time of F + H2 system

Figure 18: PE over time of F + H2 system

Figure 19: KE over time of F + H2 system

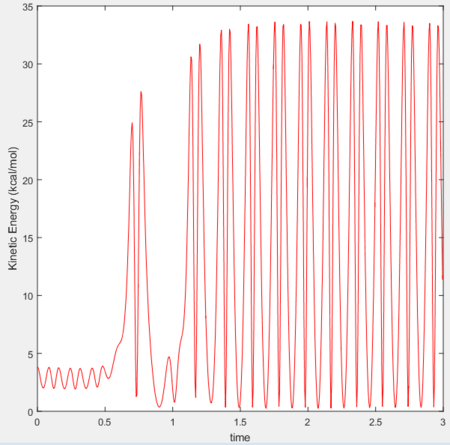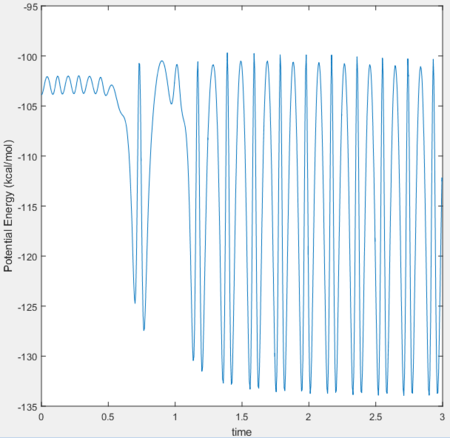
Since it has been established that the reaction is exothermic, the loss in potential energy is believed to have transferred to kinetic energy. To confirm whether conservation of energy is held for the system, the 'PE over time' and 'KE over time graph' are analysed:

	Average before collision	Average after collision	Difference
PE	-102.9	-116.48	-13.58
KE	2.835	16.9705	+14.1355

Potential energy is transferred as kinetic energy in the system.

The momenta of the system before and after the reaction can be analysed qualitatively: as F-H is formed, the amplitude of vibration is larger than that of H-H before the bond breaks. This is expected, as KE = p²/2m. The increased kinetic energy is manifested in the H-F vibration.

Experimentally, the released PE can be measured as an increase in temperature of the reaction system.

Effect of initial momenta on reactivity

F + H₂

F + H₂ was tested for p_HH in the range -3 to 3, with r_HH = 0.74, momentum p_FH = -0.5.

atom A = H, atom B = H, atom C = F

Negative Values Figure 19: pHH = -1.0000, unreactive Figure 20: pHH = -2.0000, unreactive Figure 21: pHH = -2.0570, unreactive Figure 22: pHH = -2.0571, reactive Figure 23: pHH = -2.2992, reactive Figure 24: pHH = -2.2993, unreactive Figure 25: pHH = -2.6459, unreactive Figure 26: pHH = -2.6460, reactive Figure 27: pHH = -2.9608, reactive Figure 28: pHH = -2.9609, unreactive Figure 29: pHH = -3.0000, unreactive

Positive Values Figure 30: pHH = 1.0000, unreactive Figure 31: pHH = 2.0000, unreactive Figure 32: pHH = 2.2878, unreactive Figure 33: pHH = 2.2879, reactive Figure 34: pHH = 2.4265, reactive Figure 35: pHH = 2.4266, unreactive Figure 36: pHH = 2.4306, unreactive Figure 37: pHH = 2.4307, reactive Figure 38: pHH = 2.4479, reactive Figure 39: pHH = 2.4480, unreactive Figure 40: pHH = 2.6389, reactive Figure 41: pHH = 2.6390, unreactive Figure 42: pHH = 3.0000, unreactive

From the plots, it can be concluded that there exists a discrete range of values of p_HH which leads to a reaction. These values lie between each reactive result. It should be noted that shown above was not an exhaustive result, there may be more values in between.

Using the same initial position, another plot was created with p_FH = -0.8 and p_HH = 0.1:

Figure 43, reactive

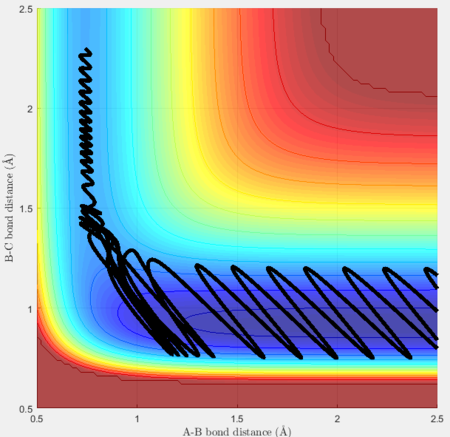
An observation can be made regarding the magnitude of p_HH that even when it is smaller, representing a lower vibrational energy, the H-F bond formed still has a high vibrational frequency.

H + HF

An optimisation of momenta was carried out for the reverse reaction with r_HH = 1.9Å, r_HF = 0.92Å.

atom A = H, atom B = H, atom C = F

Figure 44: pHH = -1.5, pHF = 10.5

Figure 45: Internuclear distances vs Time, showing the cleavage of H-F bond

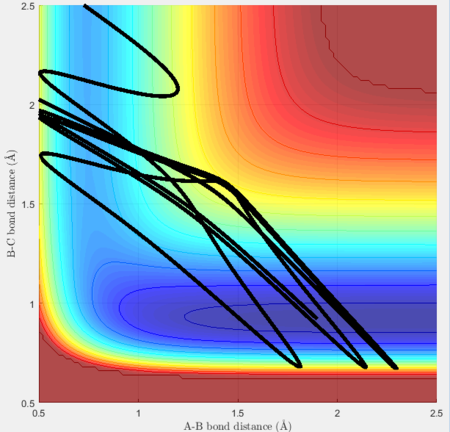Polanyi's empirical rule

Polanyi's empirical rule states that for a reaction with early transition state, energy stored in translation mode is more effective for promoting the reactants through the activation barrier; whereas for a reaction with late transition state, energy stored as vibration mode is more effective for promotion^[2]. For F + H₂, since it is exothermic, its transition state is early and thus it is favoured for reactions with high transnational energy. As for H + HF, the endothermic reaction has a late TS and vibration mode energy is more effective for its promotion through the barrier. This was demonstrated in Fig 44, where the H-F vibration was maximised while minimising the translational energy of the incoming H.

References

[1]: Jun Chen, Zhigang Sun, and Dong H. Zhang, The Journal of Chemical Physics 142, 024303 (2015)

[2]: J. C. Polanyi and W. H. Wong, The Journal of Chemical Physics 51, 1439 (1969); doi: http://dx.doi.org/10.1063/1.1672194