Molecular Reaction Dynamics: Applications to Triatomic systems

Chemical reactions can be modeled using Newtonian mechanics, ignoring quantum mechanical phenomena. Presented here is the study of 2 systems based on the linear collision of a single atom into a diatomic molecule.

H - H - H System

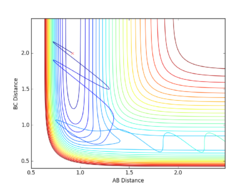
Potential Energy Surfaces

What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

The reaction path that links reactants to products follows a minimum energy. The highest energy point along this path is a saddle point known as the transition state. At this location, the two components of the gradient equal to zero, however, a deviation from the path will cause an increase in energy while movement along the path will cause a decrease in energy i.e. the second derivative in the direction along the path is negative and the second derivative perpendicular to the path is positive. In contrast, movement in any direction at the minima (reactants/products) will result in an increase in energy, the second derivative in both directions is positive.

Jas213 (talk) 01:07, 29 May 2018 (BST) It wouldn't have hurt to give some equations, but overall correct.

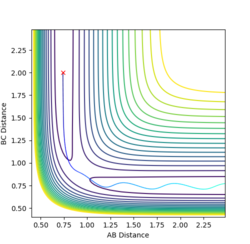
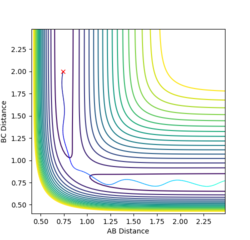
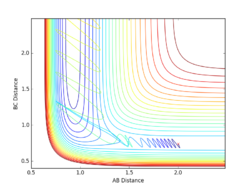
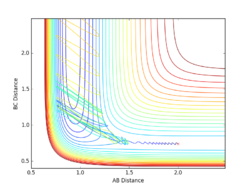
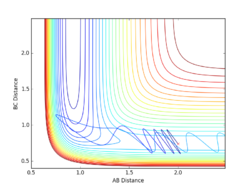
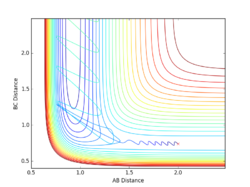
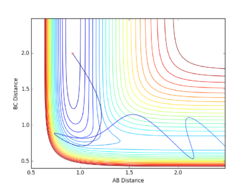
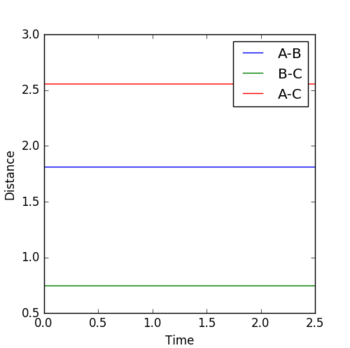
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

Given the symmetric nature of the triatomic Hydrogen system, in the transition state, r₁ is expected to equal r₂. Furthermore, at the transition state, the gradient in both directions is zero and so there should be no resultant momentum. Modifying the internuclear separation with r₁ = r₂ to minimise internuclear momentum yields an approximate value for the transition state at r_ts = 0.90774 Å. This seems a reasonable value for a state between bond formation and breaking. It is larger than the H-H bond length, but smaller than the combined Van der Waals radii of 2 H atoms.

Reaction Path Trajectories

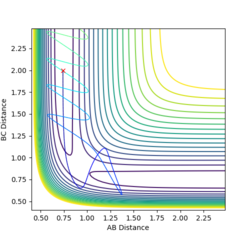
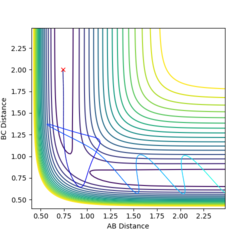
Comment on how the mep and the trajectory you just calculated differ.

In the minimum energy path calculation, the system's velocities are reset to 0 after each iteration and so the atoms move infinitely slowly. As a result, the trajectory follows the path of lowest energy without deviation. In the dynamic calculation, the velocity is conserved, manifesting as an oscillation in internuclear distance i.e. a molecular vibration.
In this case, r₁ is displaced to r_ts + 0.01 and so the atoms form the product (A + BC). When r₂ is displaced and r₁ set to r_ts, the atoms move to the reactants (AB + C).

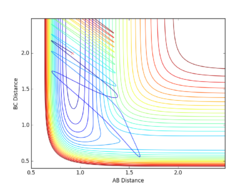
Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.

p₁	p₂	Total E /kcalmol^-1	Trajectory	Description
-1.25	-2.5	-99.018	Reactive	C approaches AB with enough momentum to react (pass through the transition state), producing molecular BC and atomic A.
-1.5	-2.0	-100.456	Unreactive	C does not approach AB with enough momentum to get over the energetic barrier and so is repelled without reaction.
-1.5	-2.5	-98.956	Reactive	Another successfully reactive trajectory. The larger difference in momentum results in slightly larger oscillation post-reaction and so a higher total energy.
-2.5	-5.0	-84.956	Unreactive	C has enough energy to pass through the transition state and form a temporary bond, however it moves so close to B that coulombic repulsion between the atoms launches it back and no reaction occurs. This is an example of "barrier recrossing", wherein the system passes through the transition state multiple times.
-2.5	-5.2	-83.416	Reactive	BC passes through the transition state 3 times, another example of barrier recrossing. The BC bond is formed then broken to induce large enough vibration in AB to break the bond, before subsequently reforming the to produce the reactants.

Jas213 (talk) 01:08, 29 May 2018 (BST) initial conditions before table and concluding comment following the table would have been expected.

Transition State Theory

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

It is assumed that:
1. Chemical reactions can be predicted using the Newtonian interactions of atoms and ignoring quantum mechanical effects.
2. Activated complexes near the transition state are in equilibrium with the reactant molecules and can be converted into the products.
3. Each time the transition state is crossed, a reaction goes to completion.

At mild temperatures, Transition State Theory (TST) will fairly accurately predict the rate of reaction. Once the temperature is elevated enough to allow for barrier recrossing however, the rate will be overestimated compared to experiment. Additionally, at lower temperatures, TST does not account for the ability of particles to undergo quantum tunneling and bypass the transition state energy barrier to react at a lower energy. Therefore, the rate of reaction may be underestimated compared to experiment.

Jas213 (talk) 01:09, 29 May 2018 (BST) Where are your references for TST?

H - H - F System

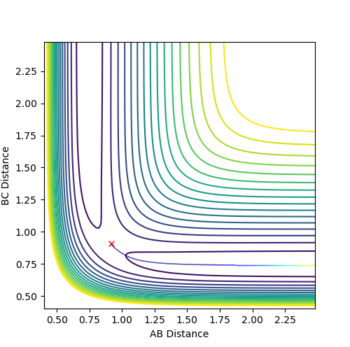
PES Inspection

Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

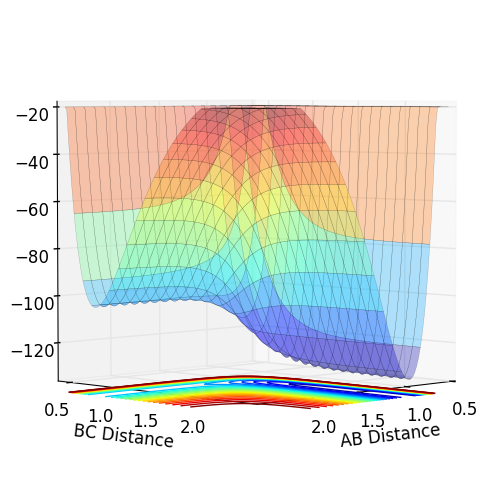
Entropic effects can be considered negligible in comparison to enthalpy as both products and reactants involve 2 species, one monatomic and one diatomic. The depth of valleys indicate a total energy of -104 kcalmol_-1 for H-H + F and -134 kcalmol_-1 for H + H-F, hence the reaction of F with H₂ is exothermic and the reaction of H with HF is endothermic.

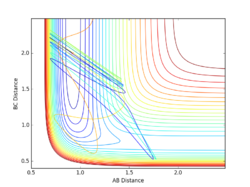
Locate the approximate position of the transition state.

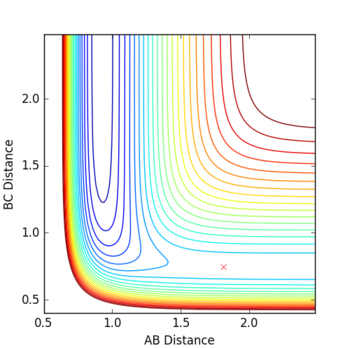By changing r₁ and r₂ to minimise internuclear momenta, the transition state can be located. By using Hammond's postulate, one can assume that the transition state more closely resembles F + H-H as it is closer in energy to this configuration. The resulting values are r_HH = 0.744888 Å and r_HF = 1.810748 Å.

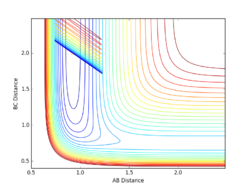
Report the activation energy for both reactions.

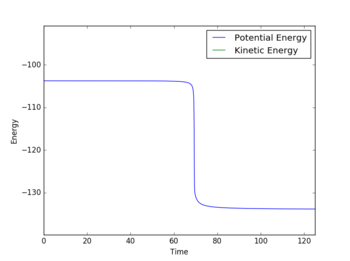The energy of the TS was found to be -103.752 kcalmol^-1. The energy at the minimum H + H-F was -134.025 kcalmol^-1 and hence the activation energy for the reaction of H with H-F is 30.273 kcalmol^-1. The energy at the minimum H-H + F was -103.995 kcalmol^-1 and so the activation energy for the reaction of H-H with F is 0.243 kcalmol^-1. Jas213 (talk) 01:11, 29 May 2018 (BST) Very neat reply, comment on your results. Is that what you would have expected?

Reaction Dynamics

In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

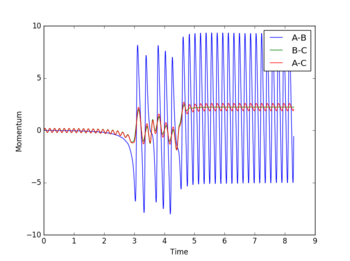
The loss of potential energy in the exothermic reaction of H-H + F to form H and H-F is converted into kinetic energy in the form of vibrational and translational motion of the atoms. This energy is subsequently dissipated to other molecules in a reaction vessel when this is carried out on a macroscopic scale. The result of this is an increase in temperature of the reaction mixture, which can be observed and measured to confirm the magnitude of temperature change is equivalent to the loss of potential energy.

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

F + H-H

Given the initial positions r_HH = 0.74 Å and r_HF = 2.00 Å, the following results were obtained when varying the initial momenta:

p_HF	p_HH	Reactivity	Follows Polanyi's Rules?
-0.5	-3.0	Unreactive	Yes
-0.5	-1.5	Reactive	-
-0.5	0.0	Reactive	Yes
-0.5	1.5	Unreactive	-
-0.5	3.0	Unreactive	Yes
-0.8	-0.1	Reactive	Yes
-0.2	-4.0	Reactive	No

H + H-F

Given the initial positions r_HF = 0.92 Å and r_HH = 2.00 Å, the following results were obtained when varying the initial momenta:

p_HF	p_HH	Reactivity	Follows Polanyi's Rules?
-1.00	-11.00	Reactive	Yes
-0.10	-11.00	Reactive	Yes
-0.01	-11.00	Reactive	Yes
-0.01	-8.00	Reactive	Yes
-11.00	-1.00	Unreactive	Yes
-11.00	-0.10	Unreactive	Yes
-8.00	-0.01	Unreactive	Yes
-10.00	-1.00	Reactive	No

Discussion

Polanyi's rules state that an early transition state requires translational energy for reaction efficiency, while a late transition state requires vibrational energy.^[1] We can apply this to the H H F system as follows: the H-H + F reaction is exothermic, therefore has an early transition state and so should require translational energy. This can be seen in the first table above: the simulations with high vibrational energy often fail. When this is reduced, however, the tendency to react increases.

In the case of H + H-F, the rules indicate that high vibrational energy is necessary. Indeed, with a high H-F vibrational energy, the reaction proceeds easily and when given equivalent translational energies and low vibrational energy, it fails.

These rules are in reality only guidelines however. The opposite case of low vibrational energy and high translational energy may also yield a successful reaction of H and H-F as in the final case above. Alternatively, in the reaction of H-H with F, a high vibrational energy and low translational energy can also yield a successful reaction.

Jas213 (talk) 01:14, 29 May 2018 (BST) Why could this be? Why can the very high values of momenta contradict Polanyi? Overall good discussion, clear description of your working.

↑ R. D. Levine Molecular Reaction Dynamics, Cambridge University Press, 2005

[1] R. D. Levine Molecular Reaction Dynamics, Cambridge University Press, 2005

[1]