MRD:Hajera

EXERCISE 1: H + H₂ system

1. What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

The total gradient, $\frac{dV}{d{r}_i}$ , at both a minimum and a transition state (TS) is zero. However, looking at their second derivatives allows them to be distinguished. As the transition state is the maximum on the minimum energy path (i.e. it is a saddle point):

$((\frac{{\partial }^{2}V(r)}{\partial r_{ab}^2}.\frac{{\partial }^{2}V(r)}{\partial r_{bc}^2})-(\frac{{\partial }^{2}V(r)}{\partial r_{ab}\partial r_{bc}}{)}^2)<0$.

However, for a minimum:

$((\frac{{\partial }^{2}V(r)}{\partial r_{ab}^2}.\frac{{\partial }^{2}V(r)}{\partial r_{bc}^2})-(\frac{{\partial }^{2}V(r)}{\partial r_{ab}\partial r_{bc}}{)}^2)>0$ AND $\frac{{\partial }^{2}V(r)}{\partial r_{ab}^2}>0$

Nf710 (talk) 13:25, 9 June 2017 (BST) This is correct but it needs to be in the basis of normal modes, one of these modes is the reaction coordinate

2. Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.

Figure 1: A plot of Internuclear Distances vs Time for the TS shows the internuclear distances are constant, due to no kinetic energy, with initial conditions r1 and r2 = 0.9077 A.

Figure 2: The potential energy at the transition state is constant (to the 6th decimal place, -99.304731 kcal/mol) as it is a maximum and there is no interconversion between KE and PE.

The transition point was deduced from observing the initial bond distances which led to no change in internuclear distance. As the H + H₂ potential energy surface is symmetrical, the two bond distances at the TS are equal. The zero gradient at the TS translates into there being no change in potential energy energy at this point. Thus, potential energy is at a maximum, constant and there is no kinetic (vibrational or translational) energy, leading to no overall force, and the internuclear distances are constant. The conditions which were found to give this were internuclear distances of AB and BC both being 0.9077 A. The potential energy at the TS is -99.3 kcal/mol.

3. Comment on how the mep and the trajectory you just calculated differ.

Figure 3: Left: mep trajectory Right: dynamics trajectory

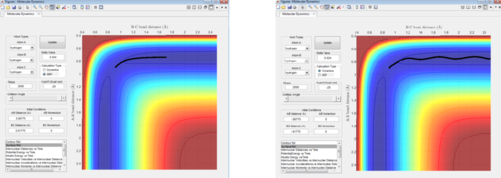
The mep is a roughly straight line while the dynamics has a wiggly trajectory. Also, for the same number of steps the mep trajectory proceeds a smaller distance than the dynamic one. These differences are a result of the mep only following the minimum energy potential path (hence its name) which leads to a constant bond length, while the dynamics is more realistic by allowing a bond vibration (which leads to an oscillating potential). The mep calculation resets momentum to zero at each step hence it takes a lot longer for trajectories to proceed. This impact can be seen by observing the intermolecular momenta against time for the two trajectories.

Figure 5: The dynamic trajectory has an oscillating internuclear momentum between atoms A and B i.e. they are bonded and have a vibrating bond.

Figure 4: The mep resets internuclear momenta to zero at each step.

4. Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.

A reaction was determined to be reactive if the trajectory crossed the activation barrier and remained on the products side.

Figure	p1	p2	Reactive?
6	-1.25	-2.5	Yes
7	-1.5	-2.0	No
8	-1.5	-2.5	Yes
9	-2.5	-5.0	No
10	-2.5	-5.2	Yes

In each of the trajectories, atoms A and B are bonded and have p1, while atom C approaches with p2. Descriptions of each trajectory are in the figure captions.

Figure 6: As C approaches A-B the trajectory is initially a straight line as the A-B bond is not vibrating. The activation barrier is successfully surpassed and atom A moves away from the newly formed B-C which has a vibrating bond.

Figure 7: C approaches the vibrating A-B molecule but fails to collide successfully. The TS is not reached and C moves away from A-B again.

Figure 8: C approaches the slightly vibrating A-B, successfully collides and the B-C bond has a greater amplitude of vibration than the A-B bond.

Figure 9: C approaches a non-vibrating A-B, the transition state is reached (so an A-B-C activated complex is formed) however C dissociates from the complex and a vibrationally excited A-B molecule is left.

Figure 10: C approaches a non-vibrating A-B, collides to form an A-B-C complex with high kinetic energy before A dissociates to leave the highly vibrationally excited B-C product.

5. State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

The main assumptions of the transition state theory (TST) are:

• Behaviour follows predictions of classical mechanics
• The system will pass through the saddle point of the potential energy surface
• The activated complexes will be in equilibrium with the reactants

Following classical mechanics assumes that unless atoms/molecules collide with enough energy to form the transition structure, then the reaction does not occur. However, according to quantum mechanics, there is a possibility that particles can still tunnel across the barrier. With respect to chemical reactions this means that there is a chance that molecules will react, even if they do not collide with enough energy to traverse the energy barrier. This effect is only noticeable for reactions with small activation energies (as probability decreases exponentially with increasing barrier height), so experimental values of rate will potentially be higher than that predicted by the TST.

The assumption that the system passes through the saddle point is incorrect, as visible in figure 10. It is also assumed that all reactions with enough kinetic energy to surpass the activation barrier will be successful, however this is false as seen in figure 9. This is because the energies must be properly distributed otherwise the barrier can be recrossed and lead to an unsuccessful collision.

EXERCISE 2: F - H - H system

6. Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

F + H₂ -> HF + H : Exothermic. A large amount of energy is released in this reaction because the F-H bond formed is far stronger than the H-H bond broken. The stability of the H-F bond arises from the large electronegativity difference between H and F.

H + HF -> F + H₂  : Endothermic. This is the reverse of the above reaction therefore the energy required to break the H-F bond is far greater than what is gained from the created H-H bond, thus the reaction requires energy.

7. Locate the approximate position of the transition state.

Figure 11: Shows the internuclear distances. They are constant for 8 seconds - indicating the TS as there is no KE - but eventually the atoms fall down the potential energy well.

By following Hammond's Postulate, the high exothermicity of the F + H₂ -> HF + H reaction means the TS will resemble the reactants more than the products. Thus, the internuclear distances for the TS here are not equal.

The transition state is found when the bond distance between F and H1 is 1.810694 A and the distance between H1 and H2 is 0.745 A.

8. Report the activation energy for both reactions.

The PE of the TS is -103.75 kcal/mol.

The PE of the reactants (F+H2) is -104.02 kcal/mol.

The PE of the products (H+HF) is approx. -133.92 kcal/mol.

Thus the activation energies are:

F + H₂ -> HF + H : 0.27 kcal/mol

H + HF -> F + H₂  : 30.1 kcal/mol

The activation energy is very small for the exothermic reaction so will have a large number of successful reactions and a high rate of reaction, while the converse is true for the endothermic reaction.

9. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

The idea that energy is conserved means that there is always an interchange between potential and kinetic energy - if kinetic energy is lost then it is converted to potential energy within the system. As the reaction proceeds, the potential energy of the system decreases, and the corresponding amount of kinetic energy is gained. This gain of kinetic energy can be measured from the temperature of the system using calorimetry. Alternatively, the vibrationally excited product molecules will deexcite and release energy in the IR region which can be measured using IR chemiluminescence.

10. Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

For a reaction to proceed, it must have enough energy to get past the activation energy barrier. This energy can be distributed as translational and vibrational energy. Polanyi's rules state that for a transition state closer to the reactants, having a great amount of translational energy leads to more success surpassing the barrier than having a large amount of vibrational energy. Conversely, when the TS is closer to the products then vibrational energy leads to greater success than translational energy.

In terms of the system being studied, as stated earlier, the F + H₂ reaction is exothermic, and according to Hammond's postulate has a TS nearer the reactants. Thus favouring translational energy over vibrational energy results in a reactive trajectory.

The opposite applies to the endothermic HF + H reaction which has a late transition state: increasing vibrational energy and not translational energy results in a reactive trajectory.

Screenshots.

Obviously you ran out of time here as you didnt prove polyanis rules, you understanding is good though. Other than that this was a good report.