MRD:Fionn's Wiki
Exercise 1: The H2 + H system
Great report overall. To top this report, I would advise referencing in various sections. Mys18 (talk) 00:20, 23 May 2020 (BST)
Defining the Transition State on the Potential Energy Surface
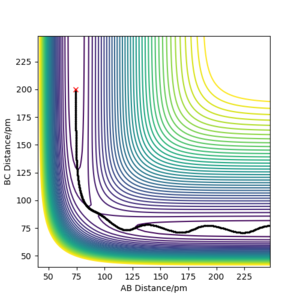
The Potential energy surface shows the minimum energy path that links the reactants to the products, the reaction coordinate. This can be seen as the path highlighted in black on plot 1. Along this path lies the transition state, which is a stationary point that is the maximum point along the reaction coordinate, and the minimum point along a path orthogonal to minimum energy path. This point is known as a saddle point, and is defined mathematically as the point where: ∂V/∂(AB distance) = ∂V/∂(BC distance) = 0, the second partial derivative of the line along the reaction coordinate is less than zero since it is a maximum and the second partial derivative on the line orthogonal to the reaction coordinate will be positive since it is a minimum point.
Excellent and concise!Mys18 (talk) 23:46, 22 May 2020 (BST)
Estimating the Position of the Transition State
Because the surface plot for the H2 + H reaction is symmetric and therefore the transition state has to be symmetric so the distances between AB and BC are equal. An initial estimate of 90 pm was chosen from the graph as this appeared to be the point that the reaction pathway passed through where the distances between all particles was equal. A plot of inter nuclear distances vs time was plotted and the internuclear distance was adjusted using trial and error until the graphs were flat and no force was acting on the molecules, fig 2. The estimated value for transition state position, rTS was 90.775 pm.
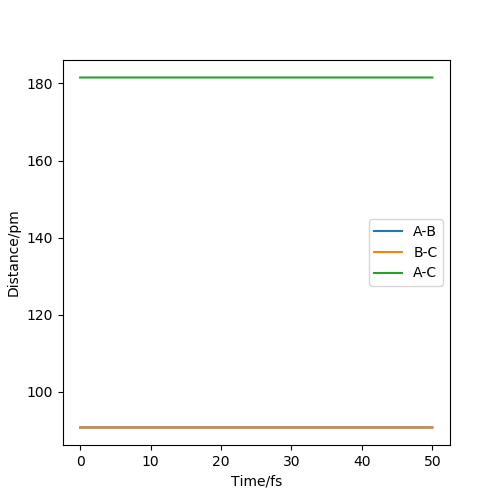
Good. May be worth relating your explanation to Hammond's postulate. Mys18 (talk) 23:50, 22 May 2020 (BST)
Calculating the reaction path
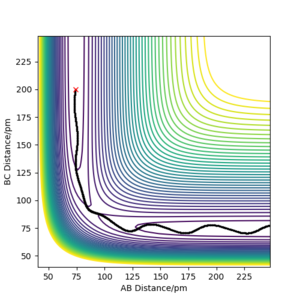
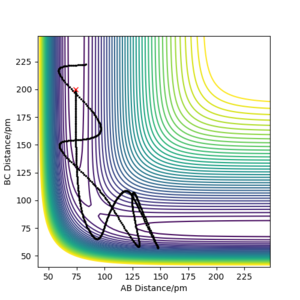
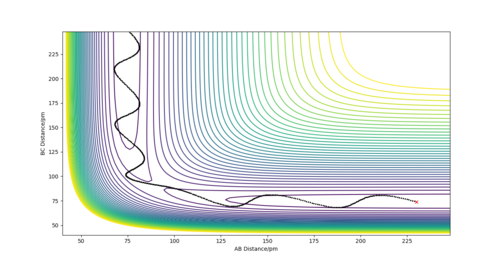
There are two calculations for the reaction path, the minimum energy path (mep), fig 3, and the dynamic path, fig 4. The minimum energy path is the path that assumes the particles are moving infinitely slowly. It does this by resetting the momentum of the particles to zero after each step. In the dynamic calculation the momentum after each step carries over and builds up throughout the reaction. The conditions for the calculations used the value estimated for rTS, but offset the rAB value by 1 pm to push the reaction in the direction of the products and the reaction pathway was calculated using both methods. The mep produced a smooth reation pathway that followed the minimum energy path all the way to the products. On the dynamic pathway the particles build up momentum which causes oscillations in the pathway. Whilst the mep is a useful tool to analyse reaction pathways, the dynamic pathway provides a more realistic insight to how the particles behave. ion pathway.
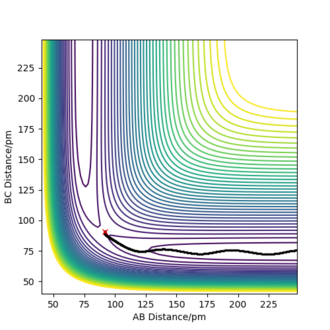
Good, it is more realistic and appreciative of realistic atom motions.Mys18 (talk) 23:53, 22 May 2020 (BST)
Reactive and Unreactive trajectories
| p1/ g.mol-1.pm.fs-1 | p2/ g.mol-1.pm.fs-1 | Etot | Reactive? | Description of the dynamics | Illustration of the trajectory |
|---|---|---|---|---|---|
| -2.56 | -5.1 | -414.3 | Yes | HC aproaches HAHB and has enough kinetic energy to overcome the transition energy barrier and HB is exchanged from HA to HC. The products then move apart in the opposite direction. | 
|
| -3.1 | -4.1 | -420.1 | No | HC aproaches HAHB and does not have enough kinetic energy to overcome the transition energy barrier, so no exchange occurs and the molecules move apart in the opposite direction. | 
|
| -3.1 | -5.1 | -414.0 | Yes | This reaction occurs in a very similar manner to the first reaction, except HAHB initially has more vibrational energy in this case. | 
|
| -5.1 | -10.1 | -357.3 | No | HC aproaches HAHB with enough kinetic energy to overcome the transition energy barrier and HB is exchanged from HA to HC, but HBHC is oscillating with enough energy that HB is transferred back to HA again and no reaction is observed. | 
|
| -5.1 | -10.6 | -349.5 | Yes | HC aproaches HAHB with enough kinetic energy to overcome the transition energy barrier and HB is exchanged from HA to HC, and then it is exchanged back to HA> and once more to HC resulting in an overall reaction of HAHB + HC -> HA + HBHC | 
|
From the table you can conclude that, although a certain threshold amount of kinetic energy is required for a reaction to occur, having energy above this threshold does not necessarily mean the reaction will occur. For example in reaction three the molecules have enough energy to react but the central hydrogen is exchanged onto one hydrogen and then back onto the other.
Good finding.Mys18 (talk) 23:56, 22 May 2020 (BST)
Transition State Theory
Transition state theory is a way of studying a reaction, by describing a path between reactants and products that passes through a maximum point, the transition state. A number of assumptions are made in this theory:
1. The reactants are in quasi-equilibrium with the transition state
2. Once a reaction has passed the transition state, it cannot reform the reactants
3. The motion of the reaction can be treated classically, ignoring quantum effects such as quantum tunneling
4. Energy is distributed in accordance with the Maxwell-Boltzmann distribution
Use of transition state theory allows us to make predictions for a reaction such as the rate constant. However there are two assumptions that may cause the calculated rate constant to be greater than the observed rate constant. Firstly, quantum tunnelling is ignored in transition state theory. Whilst this effect is relatively insignificant, it would lead to an overestimation of the rate. The main issue is the assumption that reactants can not reform the product. As you can see from the reaction trajectories calculated above, in some cases that assumption is untrue, and this phenomenon leads to a decrease in the rate that isn't accounted for in transition state theory.
Good discussion, both tunneling and recrossing are considered, and their significance!Mys18 (talk) 23:58, 22 May 2020 (BST)
Exercise 2: The H2 + F system
Pes inspection
By looking at the potential energy surface for three atoms, A = H, B = H and C = F, it is possible to determine whether the F + H2 and H + HF reactions are exothermic or endothermic. Looking at figure 5, you can see that when the BC distance is large, the energy is higher than when the AB distance is large. This tells us that H2 and F have a higher total energy than HF and H and therefore the reaction of F + H2 is exothermic and the reaction of HF + F is endothermic.
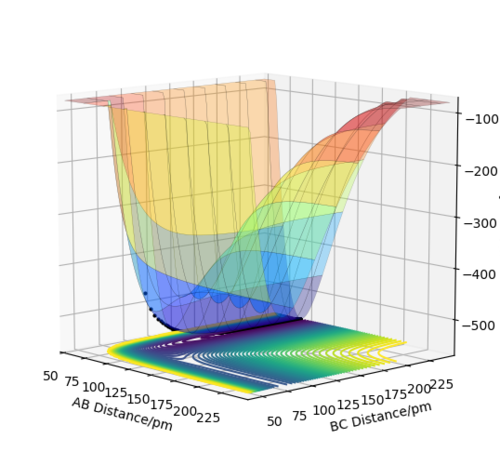
Good. How could we check this experimentally/ search the literature to justify this? (Hint: What are the bond energies for H-F and H-H?)Mys18 (talk) 00:02, 23 May 2020 (BST)
Estimating the Position of the Transition State
Hammond's postulate tells us that the transition state of a reaction resembles either the products or reactants, depending on which it is closest in energy to. In this case the reaction H2 + F is exothermic, and so it has an early transition state. This means that the transition state resembles the reactants, H2 and F. Based on this information, the H-H distance was estimated to be the bond length of the H2 molecule, 74 pm, and a BC distance of 190 pm was estimated. Using trial and error these values were adjusted until forces on the molecules were equal to zero and the graph of internuclear distance vs time was observed to be perfectly flat. This point was reached at rHH = 74.49 pm and rHF = 181 pm
Good explanation on the process.Mys18 (talk) 00:04, 23 May 2020 (BST)
Calculating the Activation energy
Once the location of the transition state was known, it was possible to find the transition state energy: -433.981 kJ.mol-1. Then we needed to find the energy of the reactants and products. To find the energy of the products, H2 and F, the HF distance was increased to an arbitrarily large number, 500 pm, and the H-H distance was made equal to the H2 bond length, 74 pm, giving an energy of -435.099 kJ.mol-1. This allowed the activation of the H2 + F reaction to be calculated as: 1.118 kJ.mol-1.
To calculate the activation energy of the reverse reaction, the energy of the products, HF and F were calculated. This was done by changing the H-H bond distance to an arbitrarily large number, 500 pm, and the H-F bond distance equal to the HF bond length, 91 pm. The resulting energy was -560.402 kJ.mol-1. Using this information the activation energy for the reaction HF + H was: 126.421 kJ.mol-1
Again, excellent description on your methodology. Well done on your estimates.Mys18 (talk) 00:06, 23 May 2020 (BST)
Reaction dynamics
Fig 7, shows the momenta vs time of a successful reaction of H2 and F, modelled using the parameters rHH = 74.49 pm and rHF = 220 pm, with initial momenta of -0.5 g.mol-1.pm.fs-1 and -1.5 g.mol-1.pm.fs-1 respectively. On the figure A-B is equivalent to H-H and B-C is equivalent to H-F. You can see that before the reaction takes place the system has some translational energy and vibrational energy in the H-H bond , but after the reaction the H-F bond has a lot of vibrational energy. This is because the reaction is exothermic and the products are lower in energy than the reactants. Energy must be conserved so this disparity is made up as vibrational energy. This can be measured experimentally using bomb calorimetry since vibrational energy is observed as heat. The amount of heat energy the reaction releases should be equal to the difference in energy of the reactants and product.
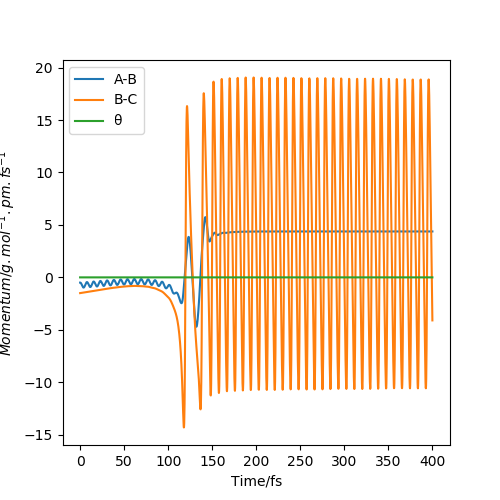
Good job. What technique looks are vibrational energies of bonds...IR perhaps?Mys18 (talk) 00:08, 23 May 2020 (BST)
How the Distribution of Energy between Translational and Vibrational modes will effect the efficiency of the reaction
The following table contains different reaction conditions for the reaction of H2 + F → HF + F. All of the reactions begin at the position rHH = 74 pm and rHF = 220 pm, with momentum pHF = -1 and momentum pHH varying in the range of -6 to 6 g.mol-1. As you can see from the table, increasing pHH, the vibrational energy of H2 increased the overall energy of the system, however it did not necessarily guarantee a successful reaction.
| pHH/ g.mol-1.pm.fs-1 | pHF/ g.mol-1.pm.fs-1 | Etot/ kj.mol-1 | Reactive? |
|---|---|---|---|
| -6 | -1 | -403.9 | No |
| -5 | -1 | -413.9 | No |
| -4 | -1 | -421.9 | Yes |
| -3 | -1 | -427.9 | No |
| -2 | -1 | -431.9 | No |
| -1 | -1 | -433.9 | No |
| 0 | -1 | -433.9 | No |
| 1 | -1 | -431.9 | No |
| 2 | -1 | -427.9 | No |
| 3 | -1 | -421.9 | No |
| 4 | -1 | -413.9 | No |
| 5 | -1 | -403.9 | Yes |
| 6 | -1 | -391.9 | Yes |
A different set reaction was tested from the same starting position with different momentum parameters. The translational energy was increased slightly by increasing pHF to -1.6 g.mol-1.pm.fs, and the vibrational energy was decreased by decreasing pHH to -0.2 g.mol-1.pm.fs. Under these conditions, a successful reaction occured, at a much lower total energy than any succesful reactions described in the table above, -433.5 kJ.mol-1, 11.5 kJ.mol-1 lower in energy than the lowest energy successful reaction described in the table above. For this reaction, it appears that increasing translational energy is more effective to obtain a successful reaction, and the reaction is more efficient.
For the reverse reaction, HF + H → H2 + F different trajectories were tested from the starting postion, rHH = 220 pm and rHF = 91 pm, the HF bond length, and the amounts of translational and vibrational energies were varied by changing pHH (translational) and pHF (vibrational). The following three trajectories were obtained:
| pHH/ g.mol-1.pm.fs-1 | pHF/ g.mol-1.pm.fs-1 | Etot/ kj.mol-1 | Reactive? |
|---|---|---|---|
| -18 | 0 | -235.6 | Yes |
| -10 | 11 | -285.9 | Yes |
| 0 | 21 | -327.5 | Yes |
These trajectories show a clear trend, that by decreasing the translational energy, pHH, and increasing the vibrational energy, pHF, the energy of the system required to obtain a successful reaction decreases, and thus the reaction is more efficient. Polyani's rules state that for a reaction with an early transition state, ie H2 + F → HF + F, translational energy is more effective at overcoming the transition energy barrier, and for a reaction with a late transition state, vibrational energy is more effective at overcoming the transition energy barrier. The calculated trajectories above demonstrate the application of these rules.
This is good. I would have begun the section with your point on what Polyani's rules states so that your description is the supporting in formation. Is there a difference in an endothermic/exothermic reaction and the corresponding degree of vibrational/transitional energies? Mys18 (talk) 00:15, 23 May 2020 (BST)