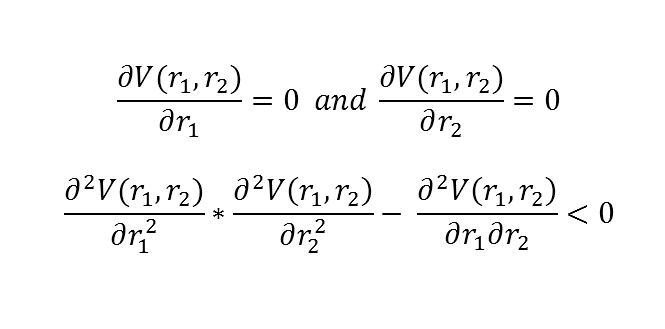MRD:Fiesta
Exercise 1: H + H2 system
On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
The transition state is the maximum on the minimum energy path. Mathematically is the saddle point of the energy surface plot, so the slopes in orthogonal directions are zero but it is not an externum of the surface. This is mathematically expressed below.
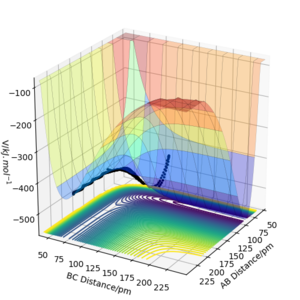
The transition state can visually be identified as the "peak within the valley" . It is within the minimum with regards to one axis, meaning it is in the "valley" where the minimum energy path lies, but it is the point where that minimum reaches its maximum, so it'll be the highest point within that "valley", as seen approximately in the middle of the picture below. It can be distinguished from a local minimum as it will be a local maximum in one axis, so it'll lie higher than the surrounding it points in one axis (in the orthogonal axis it will be the lowest point and a local minimum).
Good, clear answer but the transition state can be distinguished from the local minimum using the second partial derivative. Also, labeling your images as figures and numbering your equations, will make referring to them easier (for the reader to follow) in your text. Sf3014 (talk) 14:08, 22 May 2020 (BST)
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
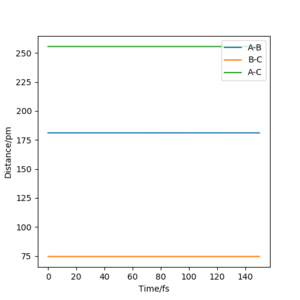
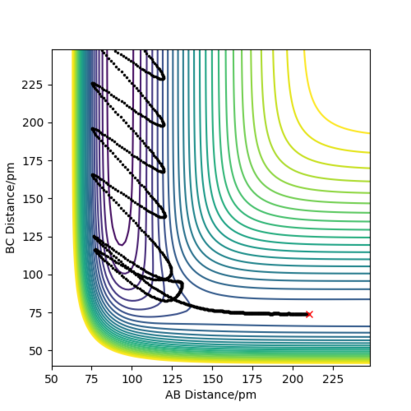
rts = 90.8 pm, as when the atoms are initially placed on the transition state position, they will not move apart from each other, only oscillate on the line of the actual saddle point. The higher their energy, the higher the oscillation, the lower the energy, the lower the oscillation and the closer they are to the actual saddle point which is the rts. As visible in the plot below of internuclear Distances vs. time, the distances are stable and they barely oscillate when the atoms are places 90.8 pm apart from each other, and hence that is my best guess for the saddle point, which is also the transition state position.
Good but you could be more accurate with your distance and you need to be clearer in your description, ie is your distance equal for r1 and r2? why? Sf3014 (talk) 14:15, 22 May 2020 (BST)
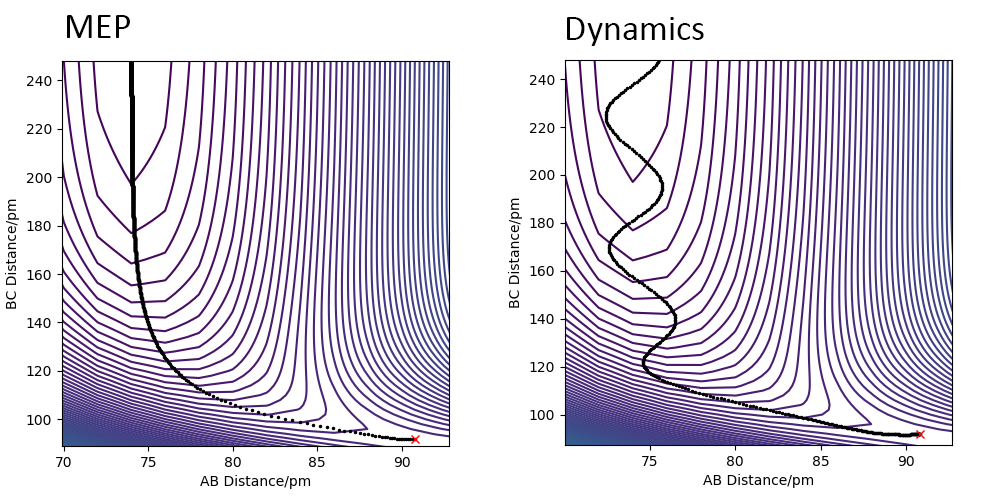
Comment on how the mep and the trajectory you just calculated differ.
The mep trajectory directly follows the very bottom of the PES, and thus has basically no oscillation, as the velocities are being artificially set to 0 in every step. This is no how it looks like in reality, as it is basically negating the effect of the gain of energy due to the reaction proceeding. In reality this gain is present, and so the newly formed molecule has additional energy that is present as vibrational energy and results in oscillations of the molecule, meaning that the reaction trajectory oscillates around the minimum energy pathway (the mep). In the diagram below, mep is on the left, dynamic calculation is on the right.
Yes there is no vibrations using the mep calculation but the velocities do not appear to be set to zero from the evidence provided. You need to choose your evidence wisely and explain you observations if it isn't clear to the reader. Sf3014 (talk) 14:25, 22 May 2020 (BST)
Look at the “Internuclear Distances vs Time” and “Momenta vs Time”. What would change if we used the initial conditions r1 = rts and r2 = rts+1 pm instead?
- The molecule that forms switches, i.e. instead of AB you get BC and instead of BC you get AB
Take note of the final values of the positions r1(t) r2(t) and p1(t) p2(t) for your trajectory for large enough t.
1000 steps, dt = 0.1 fs
| r1 | p1 | r2 | p2 | |
|---|---|---|---|---|
| mep | 74.03 | 0.0 | 217.19 | 0.0 |
| dynamics | 73.09 | 1.9788693276220095 | 733.5405120882451 | 5.0733928434002475 |
Setup a calculation where the initial positions correspond to the final positions of the trajectory you calculated above, the same final momenta values but with their signs reversed. What do you observe?
- We get back to the same initial position with the same momenta
- But not exactly, as the program likely approximates some things and rounding errors, but the values are very close
Reactive and Unreactive trajectories
r1 = 74 pm and r2 = 200 pm
| p1/ g.mol-1.pm.fs-1 | p2/ g.mol-1.pm.fs-1 | Etot / kJ mol-1 | Reactive? | Description of the dynamics | Illustration of the trajectory |
|---|---|---|---|---|---|
| -2.56 | -5.1 | -414.3 | Yes | The initial molecule oscillates slightly, and is approached by the singular hydrogen atom, they collide and a new molecule is formed that oscillates slightly more, and continues moving in the same direction, while the newly formed atom changes direction and goes back to where it came from. | 
|
| -3.1 | -4.1 | -420.1 | No | The initial molecule oscillates, the lone hydrogen approaches it but bounces off, while still relatively far and the momenta reverse, and both the molecule and atom leave heading in the direction where they came from. | 
|
| -3.1 | -5.1 | -414.0 | Yes | The initial molecule oscillates and it and the hydrogen atom approach each other, when they are all briefly at roughly similar distances and the new molecule forms and the new lone hydrogen goes back in the direction it came from. The new molecule continues in the same direction as the old one (where the old singular atom came from) and oscillates slightly more. | 
|
| -5.1 | -10.1 | -357.3 | No? | The initial molecule and the hydrogen approach with little oscillation. The molecule seems to stretch itself just as it approaches the hydrogen. We can see from the contour graph that it crosses the saddle point very far from the minimum energy needed to cross it. A new molecule is formed and has great oscillations, the new lone hydrogen seems to be leaving, but then stops and approches the newly formed molecule. There is another collision and the new molecule is broken apart and the old one is formed. It and the lone hydrogen return in the direction they came from with large oscillations. | 
|
| -5.1 | -10.6 | -349.4 | Barrier recrossing | The initial molecule approaches the hydrogen quickly with almost no oscillation. The hydrogen in the middle is seemly passed to the lone hydrogen, it bounces from it and all 3 hydrogen end up almost equidistant. Then the initial molecule reforms for one oscillation, after which the middle hydrogen joins with the initially lone hydrogen, and from a almost stationary oscillating molecule, while the newly generated lone hydrogen leaves going in the direction it came from. | 
|
Note that the total energies seem to oscillate very slightly during these calculations, so the total energy might be slightly off. Good table layout but the reactive section for rows the 4th and 5th is not clear, is it reactive or not? Sf3014 (talk) 14:39, 22 May 2020 (BST)
What can you conclude from the table?
It is too simplistic to say that over a certain total energy or over certain speeds, the reaction always occurs. If the reaction occurs does depend on the total energy, as there has to be enough energy to cross the transition state, but the molecules have to also have the right oscillation at the right time, and it is possible to have more energy than the minimum energy needed to cross the transition state, but still not cross it at the oscillations aren't in the right phase with the barrier crossing. Additionally, it can be seen from row 4 where the transition state is crossed twice, so in a sense the reaction does not occur, even though there is enough energy and the oscillations allow the initial molecule to cross the transition state. One can conclude that is a complex system and there has to be enough energy, and it has to be distributed in a certain way for the reaction to occur. Good conclusion Sf3014 (talk) 14:39, 22 May 2020 (BST)
Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
TST will give higher than reality predictions for the reaction rate. This is due to several reasons, in this case the main one it being that it does not account for recrossing. It operates in a "quasi equilibrium", meaning that from both side the molecules can reach the transition state, but once the reaction goes forward, it cannot go backwards. This is clearly shown to be false with the recrossing of the reaction trajectory in the examples below. So, even if TST could correctly predict the number of successful reactions, but it does not account for how many of those reactions will the revert, and hence will overestimate the actual rate.
Good description. Where did you get the information on transition state theory? Also, you should define abbreviations before using them Sf3014 (talk) 15:33, 22 May 2020 (BST)
Exercise 2: F - H - H system
PES inspection
By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
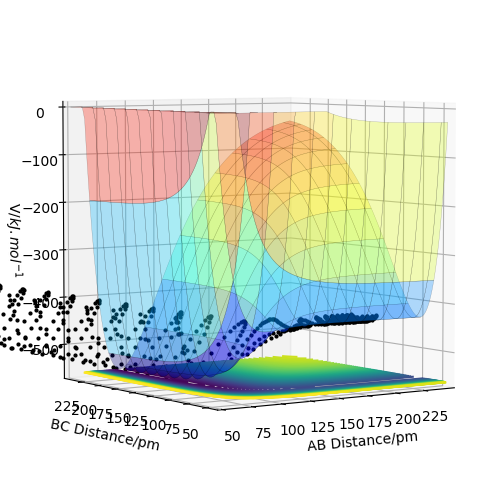
H2 + F → HF + H is exothermic and converesly, HF + H → H2 + F is endothermic, which can be seen in the image below. A is F and B and C are both H, and when AB distance is low, i.e. HF is the molecule and H is the singular atom, the potential surface is also lower than when BC distance is low, i.e. H2 is the molecule and F is the atom. As the potential energy we are working with is lower than 0, this implies that energy is needed to go from HF + H to H2 + F, and so that reaction is endothermic, and the reverse reaction is therefore exothermic.
We can approximate the exact enthalpy of a reaction by saying that they are equal to the energy released by the bond formed minus the energy used to break the previous bond. By convention, a negative number would mean that the reaction is exothermic, so for the H2 + F → HF + H reaction, we know that the enthalpy is negative, hence the formation of the new bond releases more energy than the breaking of the previous bond, so the new bond is stronger than the previous bond. Hence HF has a stronger bond than H2.
Very good, you could also back up your information on bond enthalpies using published experimental values Sf3014 (talk) 15:38, 22 May 2020 (BST)
Locate the approximate position of the transition state.
The transition state can be found by finding a position from which the molecules don't change their position with 0 momentum in a dynamics calculation, as seen in the picture below (500 steps, 0.1 fs step size). For the FHH system this was found as 181.11 pm FH distance and 74.487 HH distance. With 0 momentum the particles at the transition state don't move as it is a saddle point and so the first derivative of the potential surface is 0, so there is no net force acting on the particles.
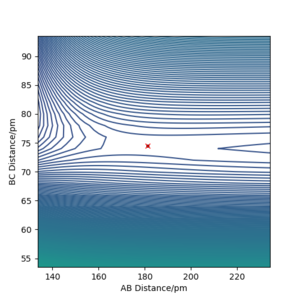
Good but refer to your images Sf3014 (talk) 15:39, 22 May 2020 (BST)
Report the activation energy for both reactions.
Activation energy can be found by performing MEP calculations from a position -1 pm (and 0 momentum) from the transition state and then looking at the energy difference from the transition state to the already formed product, so when the energy stabilizes. For the H2 + F → HF + H direction, FH distance was set to 180.11 pm and HH distance was 74.487 pm. The two energies found where -560 kJ mol-1 initially, and -434 kJ mol-1 at the transition state (note that the calculations where run in reverse, but that does not matter as we know that activation energy must be positive). This gives us a activation energy of 126 kJ mol-1.
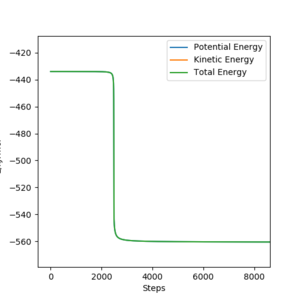
The energy that we are looking at is potential energy, but since KE is 0 in MEP, total energy is drawn over top of potential energy. For the HF + H → H2 + F direction, the transition state to H2 + F energy was looked at, with initial Fh distance at 181.11 pm and HH distance as 75.487 pm. The energy at the transition state was -434 kJ mol-1, matching the previous calculation and the final energy was approximately -434.8 kJ mol-1, giving an activation energy of 0.8 kJ mol-1.
Very good description but refer to your images Sf3014 (talk) 15:41, 22 May 2020 (BST)
Reaction Dynamics
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.
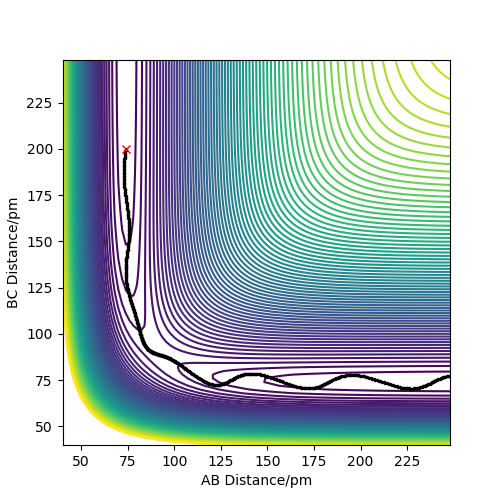
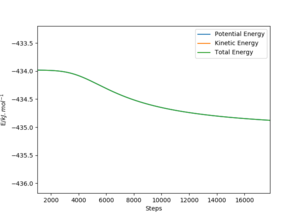
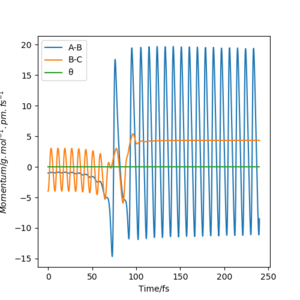
When the reaction H2 + F → HF + H occurs, thermodynamically we should have a significant release of energy. In the diagrams below, the reaction is set up with FH distance at 174 pm with -1 g.mol-1.pm.fs-1 momentum and HH distance of 74 pm with -4 g.mol-1.pm.fs-1 momentum, and this reaction successfully forms HF. From the animation it can be seen that the vibrating hydrogen molecule approaches the F atom, there are two uncertain bounces and then the new molecule is formed and the singular hydrogen atom leaves, leaving a highly vibrating HF molecule. This can also be seen in the surface plot of the reaction trajectory. We can see that the released energy from reaction takes the form of vibrations in the newly formed molecule.
The energy is converted from potential as seen in the energy surface below, to kinetic, as shown in the vibrations. These can be seen in the momentum vs time diagram, where the AB momentum oscillates greatly. This corresponds to the vibrating HF molecule, and is where the energy goes.
Experimentally this would manifest by an increased temperature and heat being given off by the reaction, and overtones in the IR as the newly formed molecules would be excited vibrationally, and also have high translational motion. This is could be measured using a bomb calorimeter.
Good but how will you use IR spectroscopy and bomb calorimetry as the reaction proceeds? Sf3014 (talk) 15:47, 22 May 2020 (BST)
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
Polanyi's empirical rules, in simple terms, are that for an early transition state (i.e. an exothermic reaction) translational energy is more useful for generating a successful reaction rather than vibrational energy. They also state that the opposite is true, that is that for a late transition state (i.e. an endothermic reaction), vibrational energy is more useful for promoting a successful reaction than translational energy. Of course, you still need enough energy to overcome the activation energy in any case, and you also need favourable conditions.
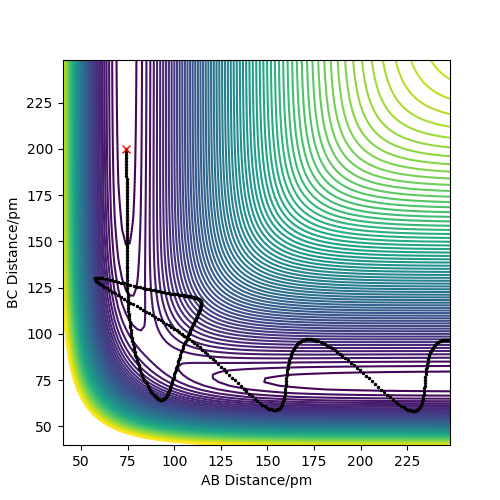
But in general, what the rules describe was also what was observed, even though it was quite difficult to get successful reactions in the first place. The exothermic H2 + F → HF + H reaction, hence early transition state, occurred more readily when the system was set up with low vibrational and more translational energy, although too much energy was also problematic, likely due to the low activation energy. The opposite reaction, HF + H → H2 + F , which endothermic, hence with a late transition state, was more successful with high vibrational energy rather than translational energy. Example plots can be seen below. Note that it was made sure for the unsuccessful reactions that the absolute amount of energy within the system was enough to cross the activation barrier.
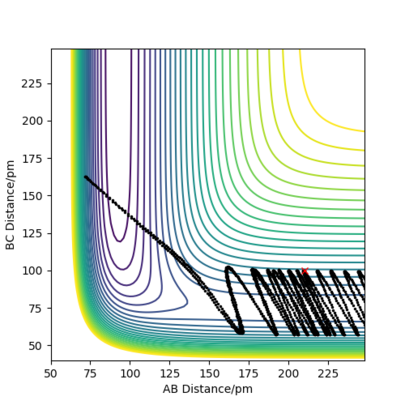
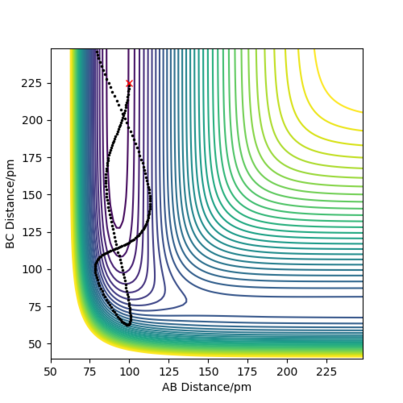
Good but there is some confusion in you image captions and there isn't enough description to see where the confusion comes from Sf3014 (talk) 16:05, 22 May 2020 (BST)