MRD:FEG17
H-H-H system
The transition state is a saddle point on a potential surface diagram. The transition state is the first partial derivative of potential with respect to r1 and r2 must be equal to 0. Any critical point will have this property, so to check if the critical point is a saddle point the values of the partial second derivative with respect to r1 multiplied by the partial second derivative with respect to r2 minus the partial second derivative with respect to r2 and r1 all squared. If the value is less than zero then the point is a saddle point. The value of this for a local minimum will be greater than zero, and the partial second derivative with respect to r1 will also be greater than zero.
For a saddle point:
The maths is correct. But it's not with respect to r1/r2. The saddle point here is 1. respect to the diagonal of r1-r2 plane (reaction coordinate) -> Maximum 2 respect to the potential energy surface -> minimum. Sw2711 (talk) 16:08, 24 May 2019 (BST)
Transition State
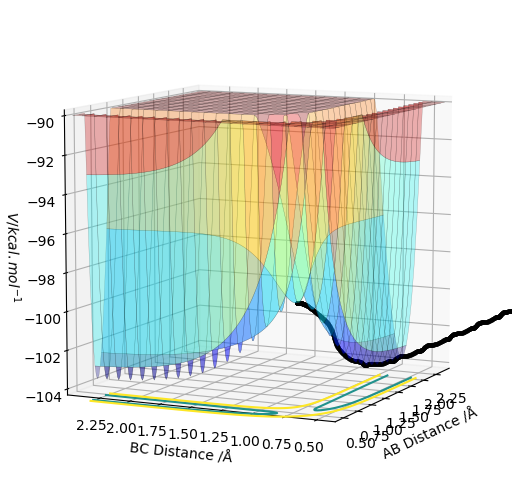
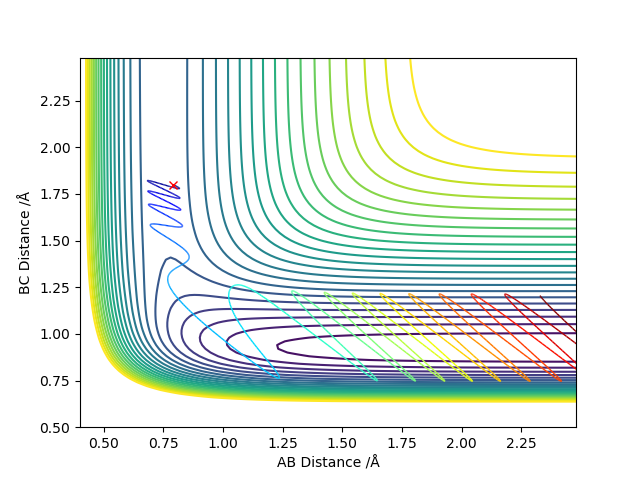
My best estimate for the value of the transition state is 0.908 Angstroms. At this distance the Internuclear Distances vs Time plot shows the kinetic energy and the potential energy as flat lines and the animation shows that the molecule is not vibrating at these values for r.
Good, but it's better to show how you get the values. Sw2711 (talk) 16:08, 24 May 2019 (BST)

MEP and dynamic
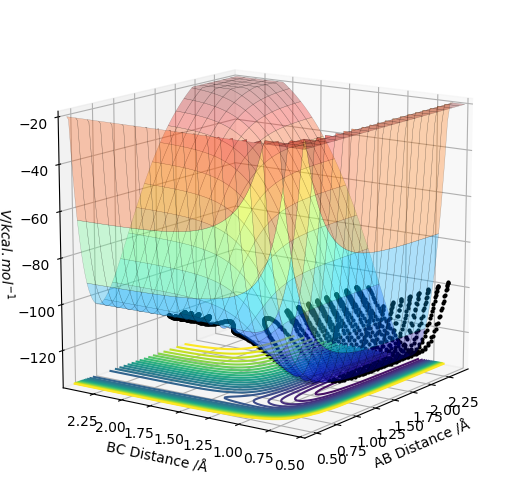
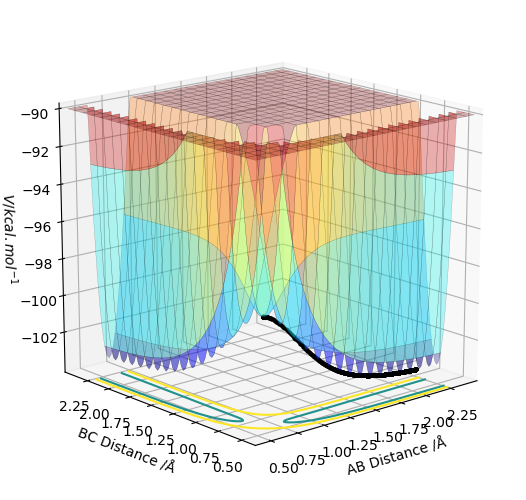
The MEP and dynamic plots were created where r1=0.918 Å and r2=0.908 Å. The MEP is the minimum energy pathway and corresponds to infinitely slow motion. In the MEP the trajectory line created is quite straight, showing no vibrational energy in the diatomic, and follows the valley floor to H1+ H2-H3. The line remains in the axes of the surface plot. When it is switched to a dynamic calculation type the trajectory line now is not as straight and oscillates from side d to side as it follows the valley floor to H1+ H2-H3. This line also is longer than the MEP line. This is due to the the fact that the momentum is not set to zero at every step and so in the dynamic image now gains momentum and velocity in every step and travels further and the greater kinetic energy. The oscillation from side to side is due to the vibrational energy in the diatomic molecule.
This part is good.Sw2711 (talk) 16:19, 24 May 2019 (BST)
The MEP surface plots:
| p1 | p2 | Etot | Reactive? | Description of the dynamics | Illustration of the trajectory |
|---|---|---|---|---|---|
| -1.25 | -2.5 | -99.018 | reactive | This trajectory was a successful reaction as there was enough energy to overcome the transition state. A reacted successfully with BC to form AB. From the plot we can see there was no vibrational energy before the reaction took place but afterwards the new diatomic gained vibrational energy from kinetic energy in the reaction. I know what you mean. But it is not a very good habit to say something to definitive like 'no vibrational energy'. You can say 'little vibration energy' instead. Sw2711 (talk) 16:26, 24 May 2019 (BST) | 
|
| -1.5 | -2.0 | -100.456 | unreactive | This trajectory was an unsuccessful reaction as the reactants did not have enough energy to overcome the transition state. The trajectory reaches the transition state but then moves back towards it came from, without forming the products. The diatomic just collides with the third atom and changes direction. | 
|
| -1.5 | -2.5 | -98.956 | reactive | This trajectory was a successful reaction as there was enough energy to overcome the transition state. A successfully reacted with B-C to form A-B. Again there was an increase in vibrational energy in the diatomic form the reaction which was transferred from the kinetic energy of the reactants. | 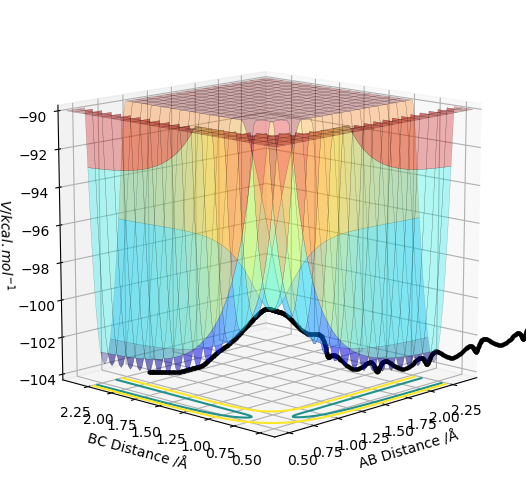
|
| -2.5 | -5.0 | -84.956 | unreactive | This trajectory was unsuccessful. The transition state was overcome initially but then the A-B bond dissociates and the trajectory turns back on itself to reform the reactants A and B-C. The energy of the reaction was the highest so far so there should've been enough energy in the system to overcome the transition state barrier. The increase in vibrational energy from the reaction in the newly formed diatomic was likely too great and so the B-C bond was broken and the reactants were formed again. | 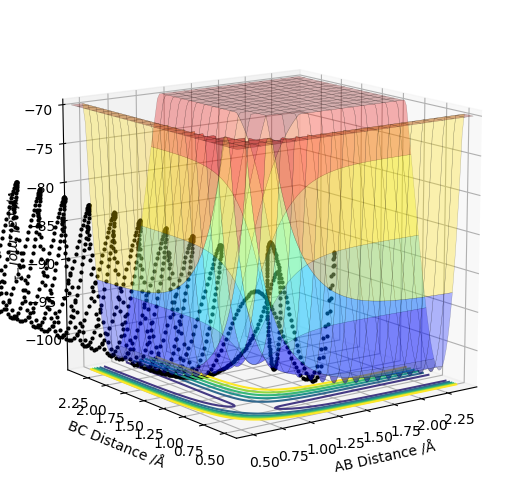
|
| -2.5 | -5.2 | -83.416 | reactive | This reaction was successful and the products were formed from the reactants. However, the reaction does not go straight from B-C TO A-B, the first time A-B is formed it dissociates back to reactants and the B atom changes direction, due to the vibrational energy being to high. This B atom travels back in the direction of atom C, reforming B-C which also then dissociates due to the high vibrational energy. This then sends B back to A for a second time and these two atoms can now react again to form the product A-B | 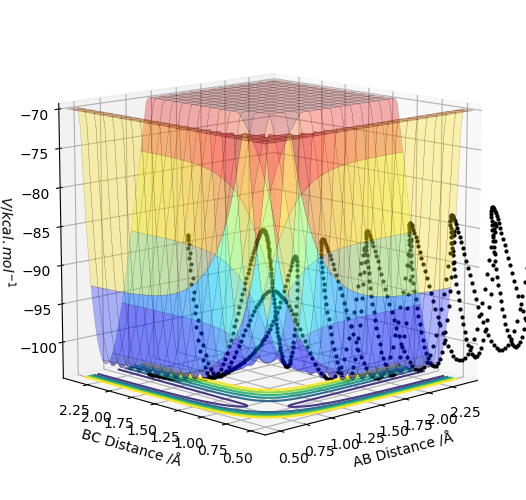
|
From this table its is clear that the energy of the system is not just enough for a successful reaction to occur as some of the higher energy systems did not produce the products as the vibrational energy in the diatomic formed was too high and so the bond dissociated. Overall this part is good. However, you mentioned couple of times here about 'high vibrational energy leads to a bond dissociate after formation and results in an unsuccessful reaction overall.', be careful with those kind of statements. Did you try 'high vibrational energy + high translational energy'; 'high vibrational + high potential energy' and other combinations, does high vibrational energy always cause a failure of the reaction? Sw2711 (talk) 16:36, 24 May 2019 (BST)
Transition State Theory
Transition State theory explains the reaction rates of elementary chemical reactions. In Transition State theory, the Born-Oppenheimer approximation is used to separate the motion of the nuclei and electrons due to the nuclei being much greater in mass. Newtons Laws of motion can be applied to the motion of the atoms in the system. An assumption is that the atoms must collide with enough energy to overcome the transition state. TS theory sates that the reactants and the activated complexes are in a quasi equilibrium with the reactant molecules. The activated complexes can convert into products and the rate of this reaction can be found using kinetic theory.1
Transition Set theory will likely work well for the first 3 scenarios in the table and so the predicted rates will likely match the real values. However, in the last two scenarios the products are formed and then go backwards beyond the transition state again. This is not allowed in transition state theory as once the products have been formed according to TS theory the products cannot reform the reactants. In TS theory the activated complexes are in a quasi equilibrium with only the reactants and not the products. The predicted rates for these two reactions will therefore likely not match the real values.
You've observed something here good about the TS recrossing. However, anything about 'distribution', 'equilibrium' etc, is it actually applicable in our case? Sw2711 (talk) 16:39, 24 May 2019 (BST)
F-H-H system
The parameters used were H1H2 (diatomic) distance = 0.74 Å, momentum = 0, H2F distance = 2.30 Å, momentum = -2.5.
This reaction is an exothermic reaction as the products, HF + H, are lower in energy than the reactants (F + H-H). This is due to the fact that in HF due to the differences in electronegativity there is ionic bonding character and the H-F bond strength is therefore much greater than H-H. When HF is formed energy is released causing an exothermic reaction. This also means that the reverse reaction HF+H to form H2 and F must be endothermic.
This part is good.Sw2711 (talk) 16:40, 24 May 2019 (BST)
Transition State
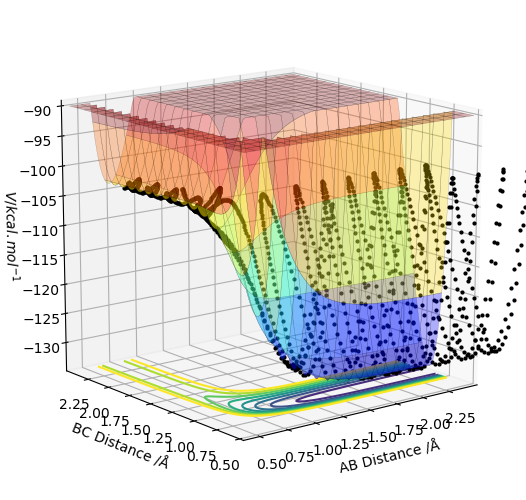
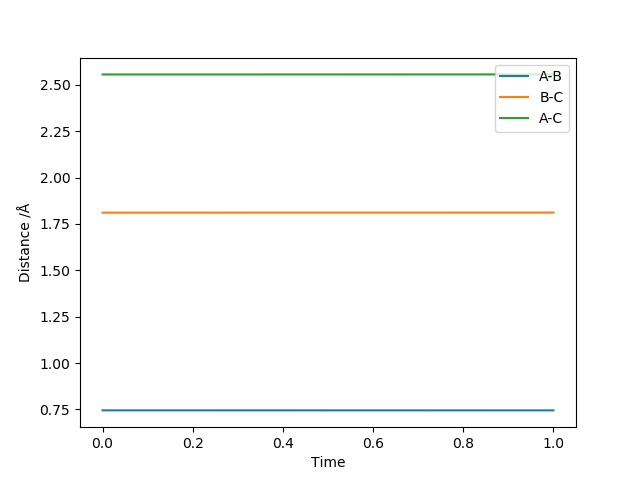
Using the parameters above this internuclear distance against time plot was produced. The transition state should be in the distance where the AB and BC lines cross over so between 0.7 and 0.8 seconds.
To find the Transition sate distances the momenta were set to zero and then AB and BC distances were varied until the internuclear distance vs time plot showed just straight lines. This was found to be when the AB distance(HH diatomic) was 0.745 Å and the BC distance(H2-F distance) was 1.811 Å. These distances correspond to the activated complex on top of the peak of the transition state.
This part is good.Sw2711 (talk) 17:00, 24 May 2019 (BST)
Activation Energy
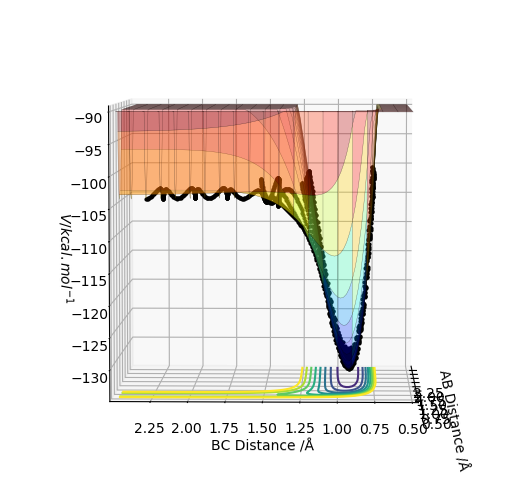
The activation energy was calculated from the energy of an MEP diagram when one of the distances was displaced from the transition state. The energy at the transition state is -103.752 kcal/mol When the HH distance was increased the energy changed to -134.002 kcal/mol. When the HF distance was increased the energy changed to -104.010 kcal/mol.
You'd better to include the MEP diagram. Also, just be aware that you can only move one of the distances, not the other one. Sw2711 (talk) 17:02, 24 May 2019 (BST)
The activation energy for H2+F to HF+H =0.258 kcal/mol.
The activation energy for HF+H to HH+F =30.250 kcal/mol.
Reaction Dynamics
A reactive trajectory, where H2 + F turn into HF + F products with the initial conditions of H2 distance=0.79 Å, momentum = 0.78 and H-F distance=1.8 Å, momentum = -0.5):
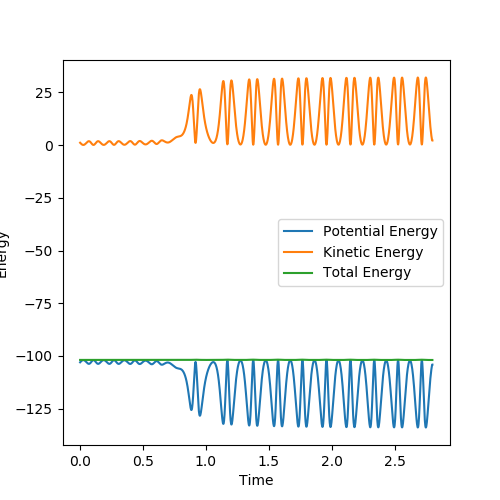
We can see from the energy vs time plot that the energy is conserved in this reaction. When the Kinetic Energy is at a maximum the potential energy is at a minimum and vive versa so the the total energy remains constant. This is also shown with the total energy line which remains flat over time. The reaction energy of this reaction will likely be emitted via heat energy. The contour plot shows that the product HF is formed and contains vibrational energy and continues to oscillate as it moves. This vibrational energy will be emitted when the HF dropped down from the vibrational state to the ground state. An FTIR spectrum could be taken of the HF sample and if a photon with an energy equal to the difference between the energies of the ground state and the vibrational state has been emitted it will be visible on the spectrum.
This part is good.Sw2711 (talk) 17:04, 24 May 2019 (BST)
The Polanyi rules states that vibrational energy is more efficient in promoting a late-barrier reaction (where the transition state resembles the products, or also known as a repulsive surface) than translational energy. For an early barrier reaction (where the transition state resembles the reactants, or also known as an attractive surface) translational energy is more efficient in promoting the reaction. Therefore, in the exothermic (production of HF) direction vibrational energy is more efficient but in the endothermic direction (production of H2) translational is more efficient.2
In the different scenarios that were set up the scenarios all followed Polanyi's rules. The exothermic reactions were driven by vibrational energy where the transition state was early, and the endothermic reactions were driven by translational energy where the transition state was late.
This part is good. But it would be better for you to show me what kind of scenarios you set up. Sw2711 (talk) 17:04, 24 May 2019 (BST)
References
1. Laidler, K. J. & King, M. C. Development of transition-state theory. J. Phys. Chem. 87, 2657–2664 (1983).
2. Zhang, Z., Zhou, Y., Zhang, D. H., Czakó, G. & Bowman, J. M. Theoretical Study of the Validity of the Polanyi Rules for the Late-Barrier Cl + CHD 3 Reaction. J. Phys. Chem. Lett. 3, 3416–3419 (2012).