MRD:EM23416
Exercise 1: H + H2 system
Distinguishing between Transition States and Minima
The transition state is a saddle point on the potential energy surface, at the maximum point along the minimum energy path between the reactants and products.
At both the transition state and the minimum points corresponding to the reactants and products the potential energy gradients with respect to both reaction coordinates will be zero, so ∂V(r1)/∂r1=∂V(r2)/∂r2=0. The transition state can be distinguished from the minimum point by taking the second derivatives of the potential energy gradient. This can be achieved by examining the Hessian matrix for the transition state, which gives a matrix
At the transition state, (∂V(r1)/∂r1)(∂V(r2)/∂r2)=0, and whereas at the minimum points (∂2V(r1)/∂r12)>0. (∂2V(r2)/∂r22)>0.
Locating the transition state
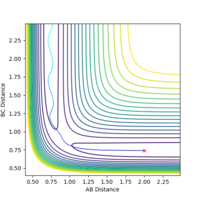
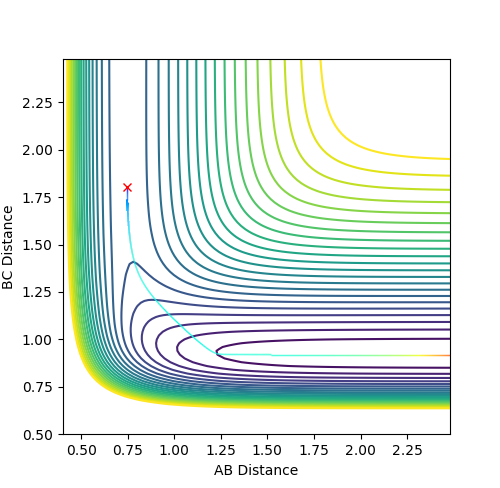
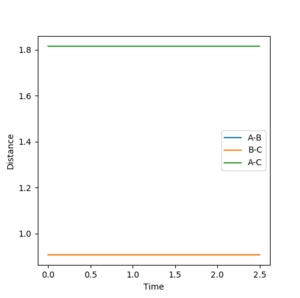
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
The transition state position is estimated as AB=BC=0.9077. As seen on the below diagram, at this position there is no oscillation in the AB or BC bond distances as only a single straight line can be seen on the graph at this value. This shows that the atoms are not oscillating at this position and therefore that there is little to no kinetic energy in the molecule, and thus the transition state has been located.
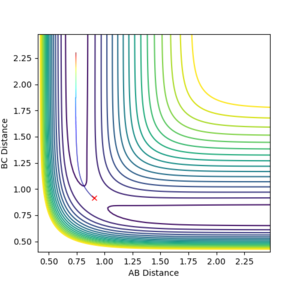
MEPs and reaction paths
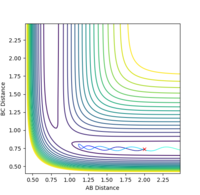
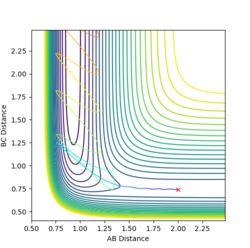
The minimum energy pathway (mep) is the pathway taken by the molecules when the momentum is consistently at a minimum value close to zero and molecules move infinitely slowly, thus kinetic energy is kept at almost zero.
This trajectory shows the actual pathway taken by the molecules as they move with kinetic energy and inertial motion. The momentum does not remain near zero in this pathway, as shown by the oscillation in the reaction path as the reaction moves away from the transition state, which is not present in the mep trajectory shown abovee.
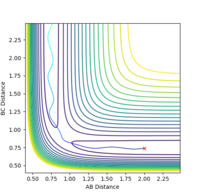
The reverse of this trajectory with using its final geometries is the e
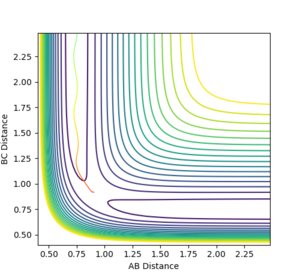
The reverse of this trajectory, using its final geometries of r1= 5.2810, r2= 0.7455, p1=-2.4810, p2= -1.5492, is its exact opposite pathway.
Reactive and Unreactive trajectories
| Reaction | p1 | p2 | Total energy (kJmol-1) | Trajectory | Reactivity |
|---|---|---|---|---|---|
| a | -1.25 | -2.5 | -99.119 |  |
This trajectory is reactive, and passes from reactants to products cleanly. The lack of oscillation visible prior to the transition state indicates that the H2 molecule has little vibrational momentum. The oscillation after the transition state shows that the H-H bond formed vibrates. |
| b | -1.5 | -2.0 | -100.456 |  |
This trajectory is unreactive, as the reaction does not progress into the product channel. The colliding molecules do not have sufficient energy to overcome the activation barrier. |
| c | -1.5 | -2.5 | -98.956 |  |
This trajectory is reactive, and the increase in oscillation visible before the transition state relative to reaction trajectory a corresponds to the increase in vibrational momentum of the starting H2 molecule. |
| d | -2.5 | -5.0 | -84.956 |  |
This trajectory is unreactive. The H2 molecule has alot of vibrational energy prior to reaction and thus oscillates strongly prior to the transition state, however the energy of the system is not enough to move fully from the transition state to the products, and thus it recrosses the barrier and the reaction doesn't progress. |
| e | -2.5 | -5.2 | -83.416 |  |
This trajectory is reactive, as the higher translational energy means that after recrossing the energy barrier, as seen in reaction d, the molecule collides with the wall of the energy surface and is able to recross the barrier again to form the products. |
Transition state theory (TST) makes 3 main assumptions: 1) The activated complex is in equilibrium with the reactants, but not the products, thus recrossing of the barrier is negligible. 2) The reactant nuclei behave as predicted by classical mechanics. 3) The reaction path will pass through the lowest energy saddle point on the potential energy surface, so multiple reaction pathways are ignored.
The key assumption of transition state theory (TST) is that the activated complex is in equilibrium with the reactants, but not the products. This means that atoms colliding with sufficient energy to overcome the activation barrier and form the transition structure will always react to form products. TST ignores all quantum mechanical behaviour of the reactant nuclei, which becomes especially prevalent in systems of light atoms such as hydrogen. This means that the values predicted by TST don't consider the tunnelling of reactant nuclei sufficient energy to overcome the activation barrier. It also means that the values won't account for particles in energy levels above the bottom of the potential well, resulting in additional zero-point energy. Both of these quantum effects effectively lower the activation barrier for the reaction and will cause experimental values for the reaction rate in this system to be higher than those predicted by TST.
Mm10114 (talk) 20:08, 31 May 2018 (BST) What is your source for the TST assumptions? You're missing a reference.
Exercise 2: F-H-H system
Reaction energetics for F + H2 and H + HF
From the potential energy surface, it can be seen that the F + H2 reaction is exothermic. This is due to the stability of the H-F bond forming during the reaction, which has a large ionic character due to the difference in the electronegativities of H and F and this strengthens it. This means that the energy released during formation of the H-F bond is greater than the energy consumed in the breaking of the H-H bond during the reaction, causing energy to be released overall. Conversely, the H + HF reaction is endothermic, as the energy released during formation of the new H-H bond can't compensate for that consumed in breaking the strong H-F bond. This confirms that the bond strength of H-F is larger than that of H-H, as seen in literature as 569.7 and 435.8, respectively.(REF)
Mm10114 (talk) 20:17, 31 May 2018 (BST) You are right. However, you report some values, what are these? Without unit these values are meaningless.
Hammond's postulate states that the transition state will be similar in structure to the reactants or products depending on which is closest to it in energy. Therefore for the early transition state of the exothermic reaction it will resemble the reactants and for the late transition state of the endothermic reaction it will resemble the products. Thus it was predicted that the transition state would be similar in structure to F + H2. The transition state was found to be at rFH= 1.8107 Å and rHH=0.7449 Å.
File:Emck f h2 mep energy vs time.png
The activation energies were found by performing an mep to either side of the transition state, and analysing the energy vs time graphs to extract the energy differences. The activation energies were as follows: F + H2 = 0.176 kJmol-1 H + HF = 30.201 kJmol-1
Mm10114 (talk) 20:17, 31 May 2018 (BST) Are you sure about the unit here? Or was it kcal mol-1 instead?
Reaction Dynamics
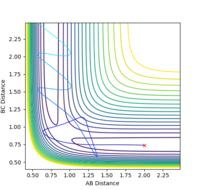
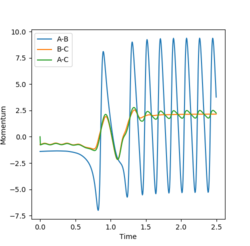
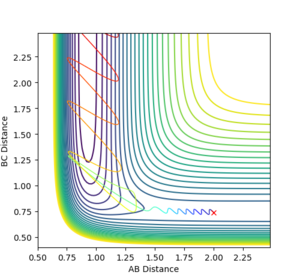
A reactive trajectory was identified for the F + H2 reaction with the following conditions, and is shown below.
rFH=2.0 rHH=0.74 pFH=-1.4 pHH=-0.75
As this reaction is exothermic, it can be expected that, due to the law of conservation of energy, the excess energy released during the reaction is converted into other forms such as heat flow to the surroundings and vibrational energy in the products. This can be seen in the internuclear momentum vs time graph for the trajectory, as the amplitude of oscillations in the H-F product molecule is much larger than in the H-H reactant, indicating that energy has been converted. The appearance of this oscillation in a graph of the momentum of the molecules also shows that the vibrational momentum and energy are closely related. This conversion of energy during the reaction could be observed experimentally via calorimetry to study the heat flow of the reaction, and thus the heat released. The difference in vibrational energy of the reactant and product molecules could be observed by IR spectroscopy, which would display overtone bands for molecules in higher vibrational states.
Polonyi's empirical rules state that vibrational energy is more efficient than translational energy in overcoming a late transition state energy barrier of an endothermic reaction, whereas translational energy is more effecient than vibrational energy for an endothermic reaction.
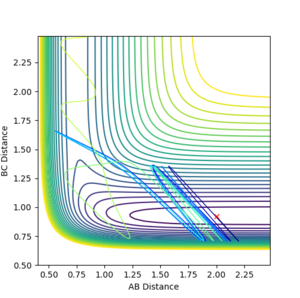
The graph below shows that significant vibrational momentum is needed to overcome the late transition barrier of the H + HF reaction, whereas translational energy is negligible.
The graph below shows that translational energy is better at promoting the exothermic F + H2 reaction, as when the translational momentum increases the reaction becomes much more feasible.
NOTE TO MARKER: Very sorry, I just forgot to add the image file links. Its been a long day.
Mm10114 (talk) 20:19, 31 May 2018 (BST) Overall good observations and stating the Polanyi's rules. However, where is the reference to the source you've taken the Polanyi's rules from? And the 'NOTE TO MARKER' completely unnecessary.