MRD:DJN160518

H + H₂ system

Q1

What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure?

Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

Minima vs Maxima

	∂V(ri)/∂ri	∂2V(ri)/∂ri2
Minima	0	>0
Maxima	0	<0

For both the transition state and the minima ∂V(r_i)/∂r_i=0 in the directions shown in the diagrams above.

To distinguish between the Minima and the Transition state we must take the second derivatives, ∂²V(r_i)/∂r_i², in the directions to investigate the curvature.

For the Minima we can see that the curvature (2nd derivative) will always be positive.

The Transition State contains a maxima along the reaction coordinate, and a minimum perpendicular to this direction.

For the Transition State we can see the Maxima along the reaction coordinate direction therefore here ∂²V(r_i)/∂r_i²>0 Everything is nice and clear up to here. Double check your little table--Sw2711 (talk) 16:39, 31 May 2018 (BST)and a Minima along the direction perpendicular to the reaction coordinate. This means our transition state is a saddle point.

Potential energy surfaces: evaluating ∂V(r_i)/∂r_i at minimum and at a transition structure:

caption

Minima 1:AB	Minima 1:BC

caption

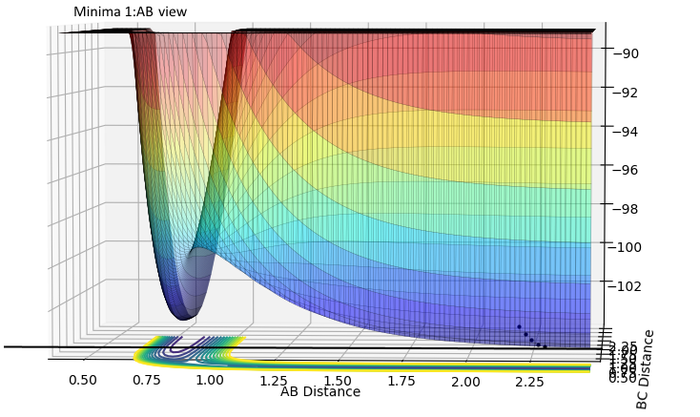Minima 2:AB	Minima 2:BC

caption

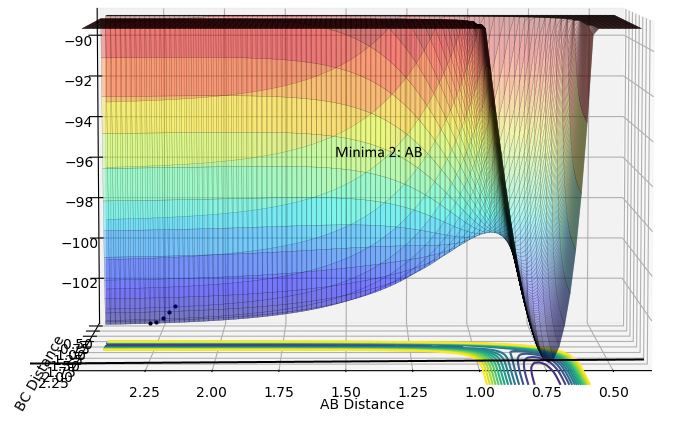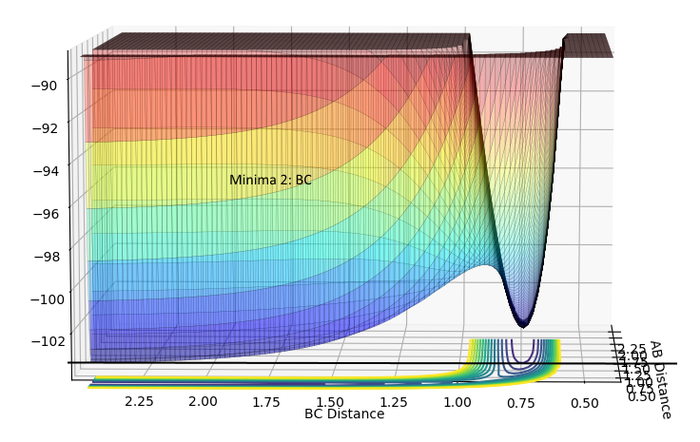
TS Maxima	TS Minima

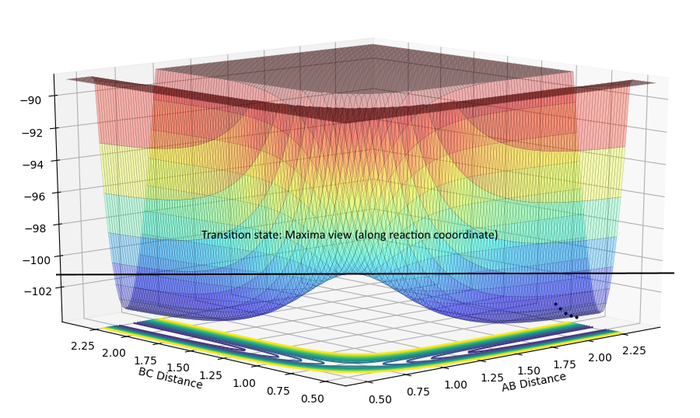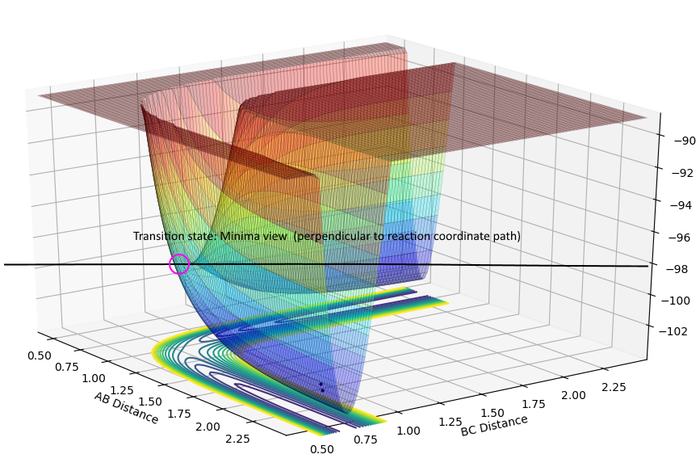
Q2

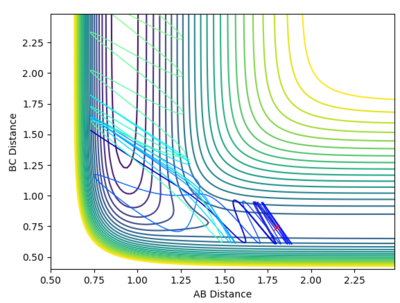
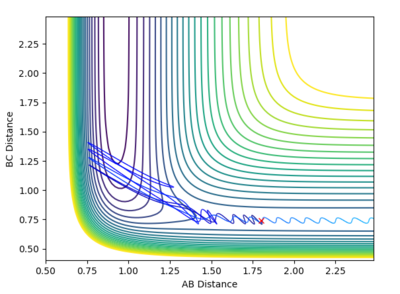
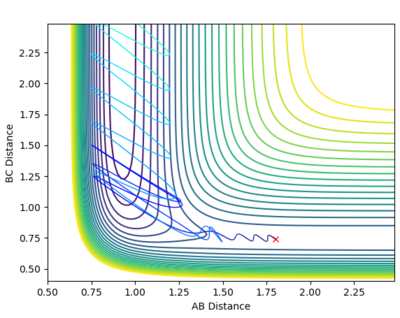
Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

At the transition state r1 = r2 (because this molecule is linear and symmetric) and from the surface plot we can see that this happens when r_ts≈0.85-0.95 Å. We also know that at the transition state the p1 = p2 = 0.0. Be careful about what you are saying here. We don't know p1=p2=0 at TS. In fact, most system passes TS with a speed. But we know TS is a saddle point, which means if we place our system with no momentum at TS, it should not move at all. Can you see the differences in the description here?--Sw2711 (talk) 16:43, 31 May 2018 (BST) Inputting this data into "LEPS GUI" and updating the "Internuclear Distances vs Time" graph with steps of r_ts +0.01 Å up from 0.85-0.95 Å allowed us to see how the graph below changed. The oscillations decreased up until r_ts = 0.91 Å indicating this is the internuclear distance r1 = r2 between H_A, H_B, H_C. I think you can do a little better to get a straight line here.--Sw2711 (talk) 16:43, 31 May 2018 (BST)

Finding r_i for the transition state

Internuclear Distances vs Time: r_i = 0.91

Q3

Comment on how the mep and the trajectory you just calculated differ.

Good--Sw2711 (talk) 16:44, 31 May 2018 (BST)

The MEP (minimum energy path) indicates the path of lowest energy for H₂ + H, thus the most favorable energy path for the system to take, however in taking an MEP we lose information about the vibrational energy of the system and we see a smooth curve that just traces the minima of the surface. In contrast, The dynamic view however displays the oscillatory behavior (due to the H_B-H_C vibrations) along the energy path, thus presenting a more realistic description of the energy path taken. The MEP resets velocity to zero at every infinitesimal increase in time along the minima of the surface. The dynamic surface presents us with the sum of the momenta at each infinitesimal increase in time along the surface thus we see oscillatory behavior.

contour plots for reaction path

Dynamics	MEP

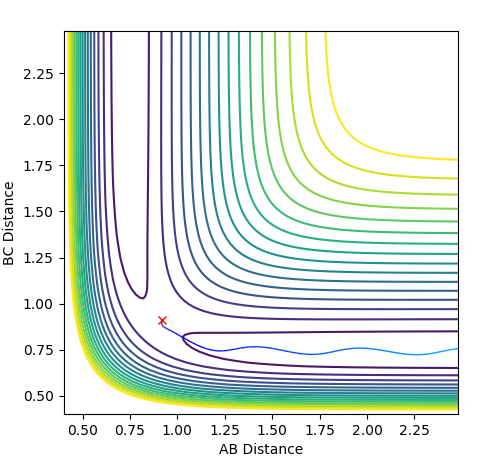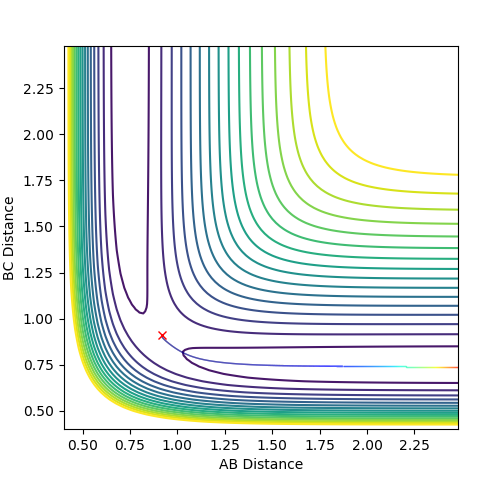
Q4

Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.

dynamic plots, independent vairable = p_i

Trajectory	p1	p2	Total Energy/Kcalmol-1	Reactive or Unreactive?	Trajectory Plot	Trajectory Discussion
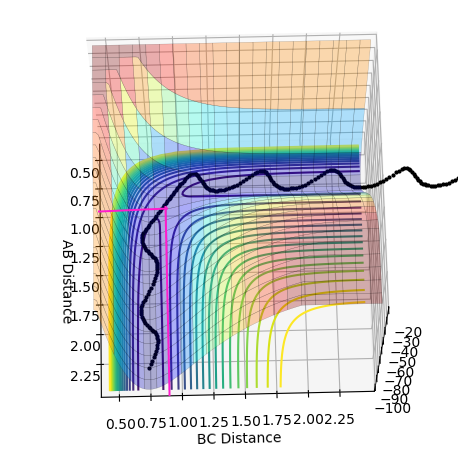
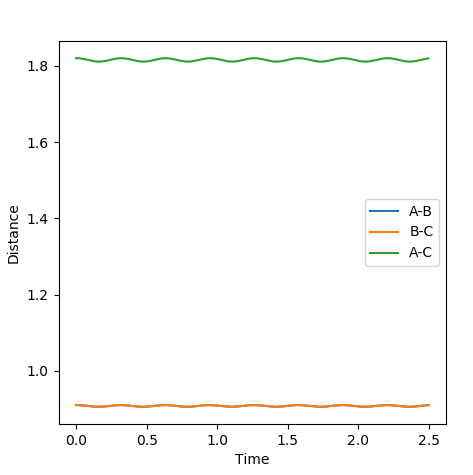
1	-1.25	-2.5	-99.018	Reactive		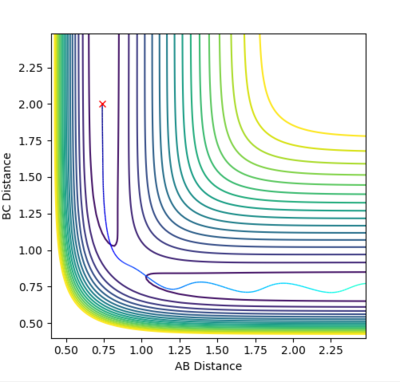We can see from the trajectory that the BC bond is formed. C approaches with enough momenta (overcoming the activation energy), collides with AB and produces A + BC forming the products. We can see in the line AB= 0.75 that there is no oscillation in the curve meaing that there is no vibration between A and B after the collision takes place.
2	-1.5	-2.0	-100.455	Unreactive		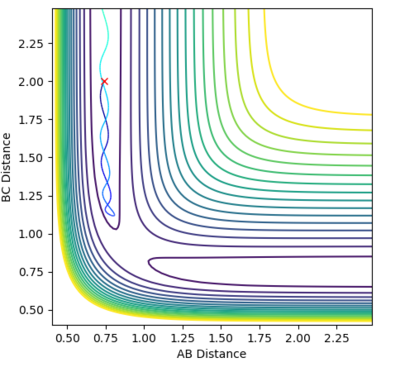No reaction occurs here (as seen in the animation) and the transition state is not overcome. Here the Vibrational energy of the AB bond is greater than in trajectory 1, and is high enough such that C (whose momentum is less than in stage 1), cannot distort the AB bond enough to form the BC bond.
3	-1.5	-2.5	-98.955	Reactive		BC bond is formed. This trajectory is very similar to trajectory 1 but we can see some vibration of AB at the line AB = 0.75 Å, meaning it must be vibrating whilst C approaches it.
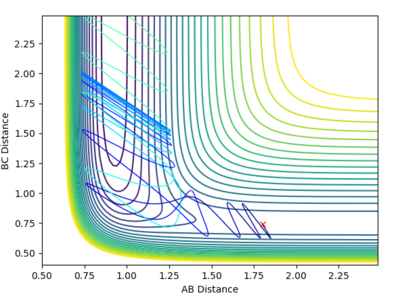
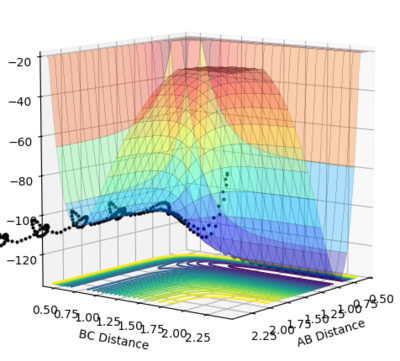
4	-2.5	-5.0	-84.954	Unreactive		The contour plot here describes more complicated behavior than what was seen previously. From the animation we see that A-B + C --> A +BC. Immediately after this we see A + BC --> AB + C and the two species move away from each other in opposite directions. (AB to the right and C to the left. This phenomena is called 'recrossing' in which the system crosses the transition state twice and we can see the odd behavior of B crossing to C then back to A again. REFERENCE:https://pubs.acs.org/doi/abs/10.1021/cr050308e. We can see from the plot of inter-nuclear distances vs time plots two points of intersection between the blue 'A-B' distance and the orange 'B-C' distance which correspond to crossing the transition state twice.
5	-2.5	-5.2	-83.416	Reactive		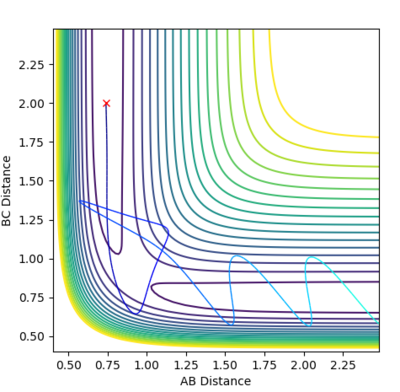The contour plot describes another recrossing process. C approaches AB with a high velocity. B then bounces to C, then back to A and then finally back to C and a BC bond is formed. This means that the transition state has been crossed three times as shown by the three points of intersection in the diagram of "internuclear distance vs time" below

Q5

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

Transition State theory

Transition State theory is used to predict ideas about the rate of reaction of a system.

Assumptions

1. Molecular systems which cross the transition state to form products can never return to reactants.

2. The lowest energy path is taken

3. Classical mechanics at the transition state

We can see from trajectory 4 that the first rule has been broken, as the transition state is crossed twice and the initial reactants are reformed. Trajectory 5 also breaks this rule as the transition state is crossed three times.

This indicates that transition state theory, whilst applicable to high energy barriers, is not as strict a theory for reactions with small energy barriers.

Both Q4 and Q5 are Good--Sw2711 (talk) 16:45, 31 May 2018 (BST)

H-F-H Section

Q1

Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

H + HF → H₂ + F

The formation of H₂ is endothermic (BC = HF). The formation of HF is therefore exothermic (BC = H₂). H₂ bond enthalpy = 435kJmol^-1. HF bond enthalpy = 569 kJmol^-1.

Good, can you work out which bond is stronger by looking at the PES?--Sw2711 (talk) 16:48, 31 May 2018 (BST)

In the graph of H₂ + H --> HF + H, the products are lower than reactants, exothermic, if we go in the opposite direction, we would form H₂ and the reaction is endothermic. Thus HF has a higher bond enthalpy than H₂.

This part is good.--Sw2711 (talk) 16:48, 31 May 2018 (BST)

Endo vs Exothermic

Formation of H2	Formation of HF
endothermic	exothermic

Locate the approximate position of the transition state.

Approximate transition state (H₂ formation)

Data	Contour plot
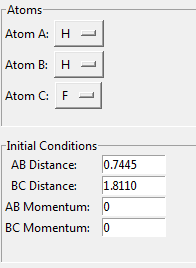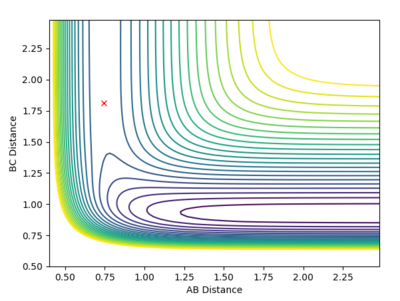
This is the data for the transition state given to 4 d.p.	Hammonds postulate:"If two states, as, for example, a transition state and an unstable intermediate, occur consecutively during a reaction process and have nearly the same energy content, their interconversion will involve only a small reorganization of the molecular structures." From Hammond's postulate and by looking at the surface plot for the formation of H2 we can see that for this exothermic reaction our transition state lies close in energy to the products, so plotting distances close to the products starting from AB = 0.75 Å and BC = 1.8 Å, we found our (approximate) transition state transition by finding the smallest "energy trail" from our starting point (marked X)in the direction of formation of H2. At the perfect transition state coordinates there would be an infinitesimally small starting point X and no reaction path as the system remains at rest at the transition state coordinates. For this formation of H2 we make the AB bond distance relatively short, and the BC distance relatively large as this corresponds the the H-F bond which will be broken if we move in the direction of the products on the contour plot.

We can see from the plot of internuclear distances with time graph that after approximately 6-8s some small change in energy causes the H₂ to be formed and the HF to dissociate

This part is good--Sw2711 (talk) 16:48, 31 May 2018 (BST)

Q2

Report the activation energy for both reactions.

E_a = E_TS - E_reactant

1)Formation of H₂

-103.76 - (-133.77) = 30.1 kcalmol^-1

1)Formation of HF

-103.76 - (-103.91) = 0.15 kcalmol^-1 You showed me how to get one sets of numbers. How about the other sets? --Sw2711 (talk) 16:49, 31 May 2018 (BST)

Reaction dynamics

Q3

i

In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

r_FH = 1.8

r_H2 = 0.74

Steps = 5000

F + H₂ Trajectories

AB momentum	BC momentum	Contour plot	Internuclear distances vs time	Discussion
-0.5	-3.0			We can see this is a reactive trajectory, forming a HF molecule. The process is exothermic and the system drops into a lower energy state. The momenta vs time graph tells indicates that at the transition state momenta of AB, BC and AC is a minimum, which is expected as we locate the transition state for a reaction when pi = 0, from this we can deduce that the kinetic energy will be minimum at this point and therefore, by the conservation of energy, potential energy will be a maximum. This PE is then converted into vibrational KE of the HF bond. These oscillations are very large indicating a loss of heat, further confirming this exothermic process.
-0.5	+3.0			We can see from the contour plot and momenta vs time graph that this is also a reactive trajectory. However, unlike before, we can now see that the transition state is crossed multiple times indicated by the minima observed in the momenta graph. The contour plot is similar to the one above but we can see that the oscillations are more dense indicating more oscillations per unit time, so the rate of transfer of energy increases. In this case the BC momentum is positive and large meaning the two Hs are trying to remain close together, this helps explains the multiple recrossing observed in this system.
-0.5	-1.0			This is an unreactive system. However we can see that the transition state has been crossed 4 times as seen in the momenta graph. Momentum of BC is negative, the total energy for the reaction is lower than previously seen, illustrated through smaller amplitudes on the momenta plot In the momenta graph we can see smaller oscillations. This is indicative of the H-H vibrations which are lower in vibrational KE than the H-F species. There is not enough energy in the system to overcome the activation energy and the smooth blue curve indicates the F atom which moves away from H2 with no oscillation.
-0.8	+0.1			This is a reactive system. We can see from this system that a small increase in the momentum of F leads to a massive increase in overall energy of the system. Which makes sense as F is much more massive than H thus as p = mv, the mF dominates. This is shown by the massive AB oscillations in the momenta plot indicating a large Vibrational KE.

So overall, what kind of experiments can you do to test your hypothesis?--Sw2711 (talk) 16:53, 31 May 2018 (BST)

ii

Trajectories to investigate momenta conditions for the formation of H₂

r_HF = 1.0 Å

r_H2 = 1.8 Å

H + HF Trajectories

AB momentum	BC momentum	Contour plot	Internuclear distances vs time	Reactive or Unreactive
5.0	-4.0		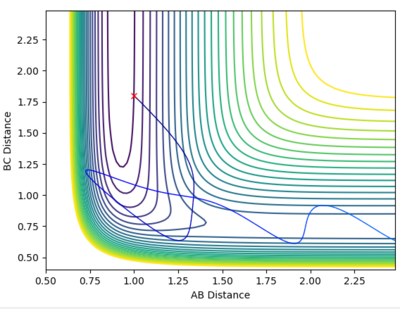	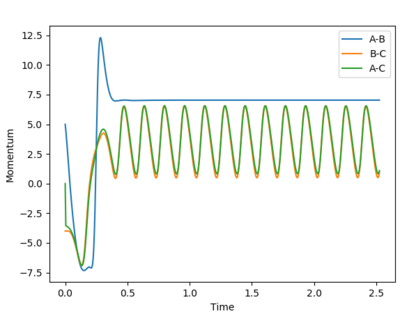Reactive
5.0	-3.0			Unreactive
3.0	-6.0			Reactive
3	-7		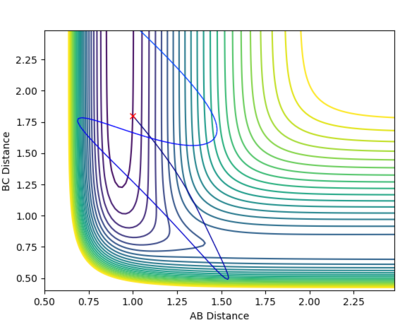	Unreactive

From this we can see that this reaction is very sensitive to changes in the translation momentum of the reacting species.

Q4

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Polanyi's rules state that:

1)For an endothermic process, the most effective way to overcome the activation energy is to increase the internal momentum of the nuclei involved in the system. This will increase the vibrational KE of the system.

- this corresponds to forming H₂, H + HF --> H₂ + F , as seen above. We saw that a small increase in the internal momentum of H-F led to a massive increase in vibrational KE along H-F and the products were formed more easily compared with just increasing the transnational KEs

2) For an exothermic process, the most effective way to overcome the activation energy is to increase the translational momentum of the nuclei involved in the system. This will increase the Translational KE of the system.

- This corresponds to forming HF, these principles are demonstrated in the graphs in the tables above.

Good--Sw2711 (talk) 16:54, 31 May 2018 (BST)