MRD:Callon
MOLECULAR REACTION DYNAMICS REPORT
EXERCISE 1: H + H2 system
Question 1
On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
The transition state is defined as the maximum on the minimum energy path linking reactants and the products. Therefore, The transition state is a saddle point on the potential energy surface. Mathematically its first derivative, ∂V(ri)/∂ri=0 , will be equal to zero and second derivative must be smaller than zero, as the transition state is a maxima. [1] As the transition state is stable, it can be distinguished from its local minimum due to the fact that the momentum of all the particles will be zero at its point.
Good but it was enough to say that the second partial derivative is less than zero at the local maximum which is how you distinguish it from the local minimum, because your final statement is true for the saddle point. Also, remember to state that these are partial derivatives Sf3014 (talk) 23:37, 1 June 2020 (BST)
Question 2
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
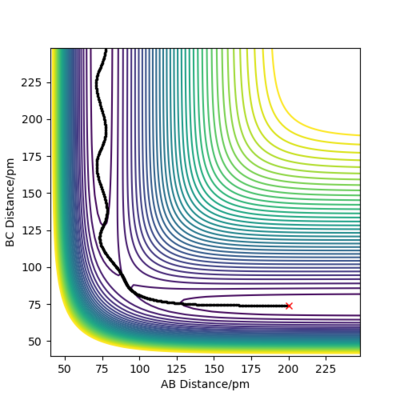
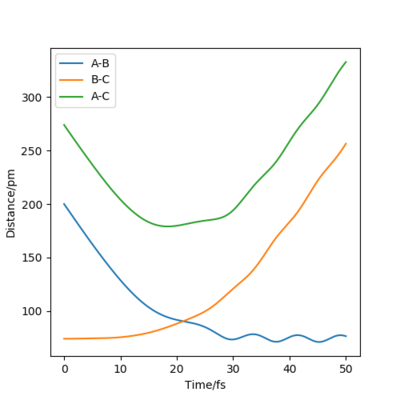
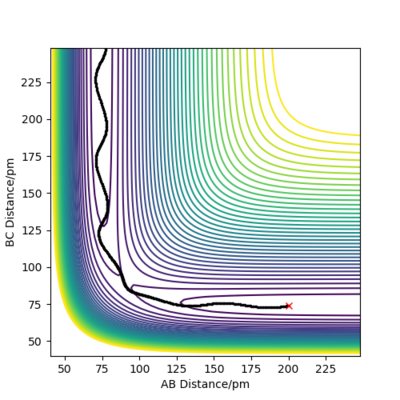
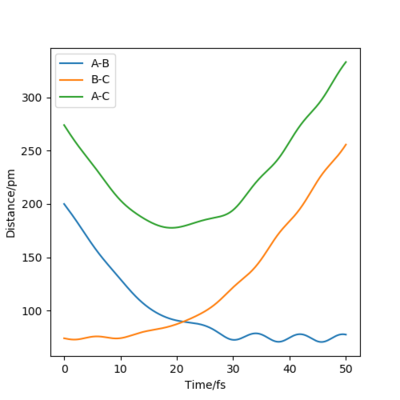
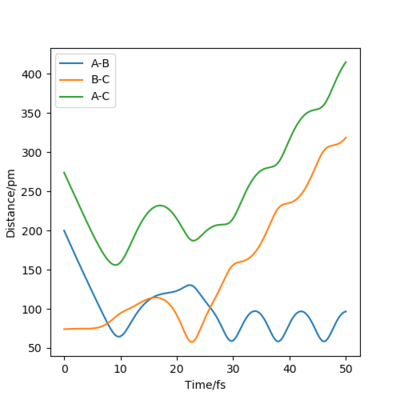
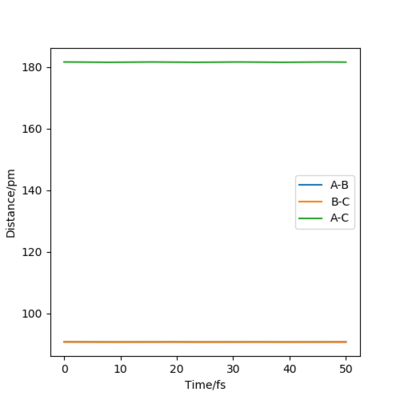
By inputting the momentum of AB=BC=0, this results in oscillations only within the potential well, and setting rAB=rBC the transition state position, rts = 90.8 pm. In the plot of Internuclear Distances vs Time, the distances between AB and AC remain constant, as the distances are constant, there is no vibrational energy. An animation of positions of atoms shows us that there is no movement of atoms and the central atom is in the process of forming one bond to one atom and breaking one bond with the other.
Good but you could be more accurate in your distances, like to 3 d.p. Did your round up the value for the distances? If so, what is the accuracy? You could show this by zooming in on your distance vs time graph or showing the forces/distances to the correct number of decimal places. Also, be clearer in your description (ie why are the AB and BC distances the same?) and refer to your figures. Sf3014 (talk) 23:44, 1 June 2020 (BST)
Question 3
Comment on how the mep and the trajectory you just calculated differ.
The Minimum Energy Path (MEP) is the defined by the direction given by the eigenvector of the smallest positive eigenvalue of the Hessian in Xmin and its corresponding continuation up to the saddle.[2] As the momentum in this simulation is zero, it can be said that the motion of the atoms is entirely driven by attractive Van der Waals interactions. Once the atoms have moved into a stable configuration, there positions do not alter, whereas in classical dynamic theory, this is not the case.
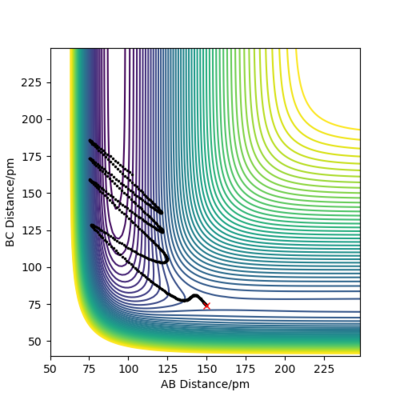
Both Figure 4 and 5 show contour plots of the potential energy surface for the system close to the transition state, where rAB = 90.8pm, rBC = 91.8pm
From Figure 4 we can see that the MEP is linear with no vibrations where as Dynamics does contain vibrations. In addition, the MEP trajectory stops at around 200 pm, whereas for the Dynamics plot, Figure 5 it has no stopping point due to momentum being conserved and has vibrations. When rAB (91.8pm) > rBC(90.8pm) the system will remain as H(A) + H(B)-H(C) whereas if rAB(90.8pm) and rBC(91.8pm) the system will more likely change to H(A)-H(B) + H(C). As both systems are modelling the same system, they both have to same potential energy.
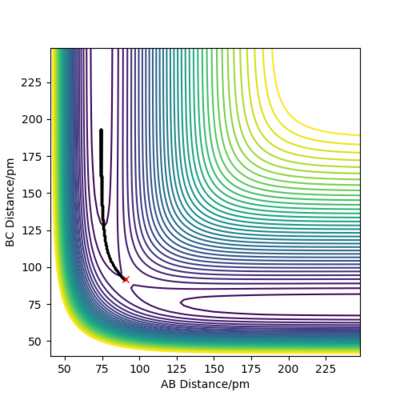
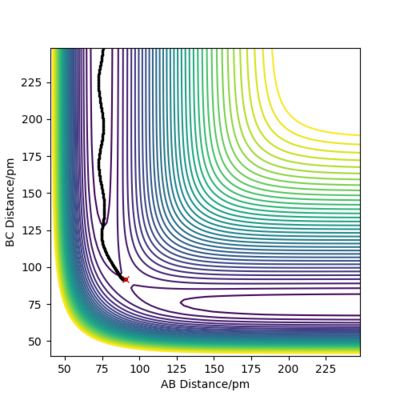
Good description on the comparison between mep and dynamic calculations Sf3014 (talk) 23:48, 1 June 2020 (BST)
Question 4
Look at the "Internuclear Distances vs Time" and "Momenta vs Time” What would change if we used the initial conditions r1 = rts and r2 = rts+1 pm instead?
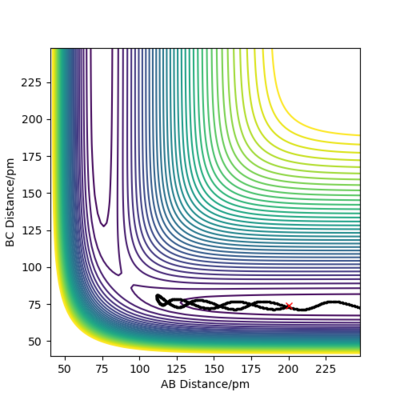
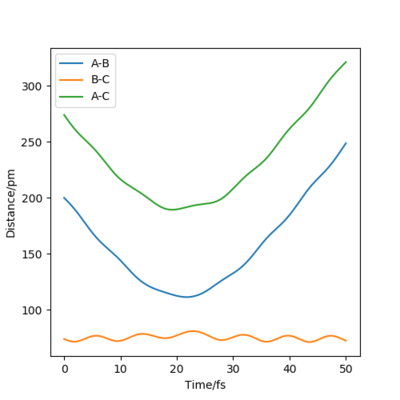
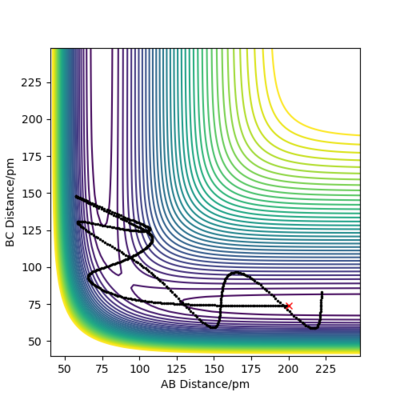
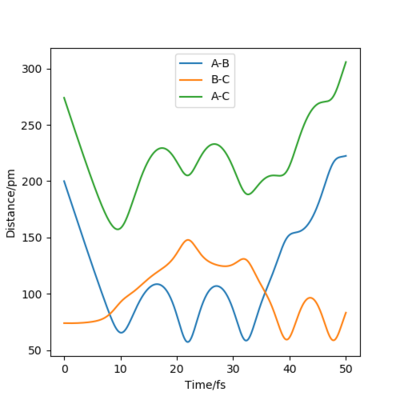
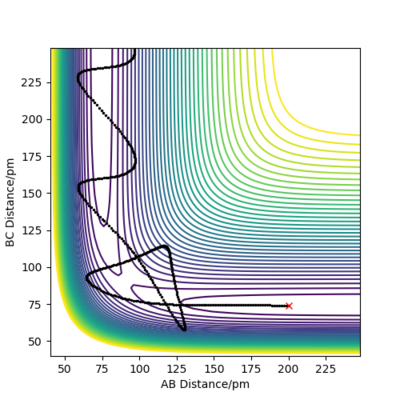
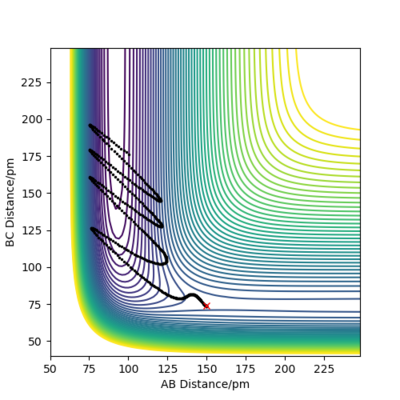
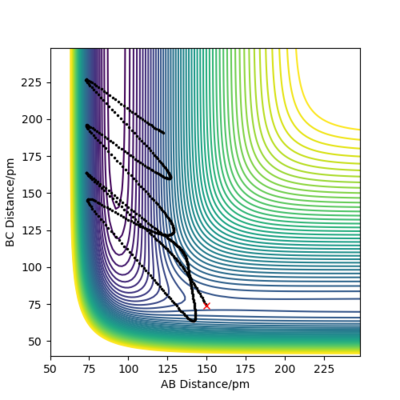
when comparing the "Internuclear Distances vs Time" and "Momenta vs Time” plots for when r2=91.8 pm, r1=90.8 pm (Figures 7 and 9) and when r1=91.8 pm, r2=90.8 pm(Figures 8 and 10), we see that the changing the parameter results in a reverse process occurring, shown by figure 6. when r2=91.8 pm and r1=90.8 pm the transition state is more of a B-C molecule due to shorter bond length. Atom C and B have more attractive forces, however they are not too close such that shorter ranged repulsive forces dominate. When r1=91.8 pm and r2=90.8 pm A-B bond length is shorter, by the same principles, A-B molecule is formed. The two different graphs can also be considered as mirror images of each other with atom B occupying the central position.
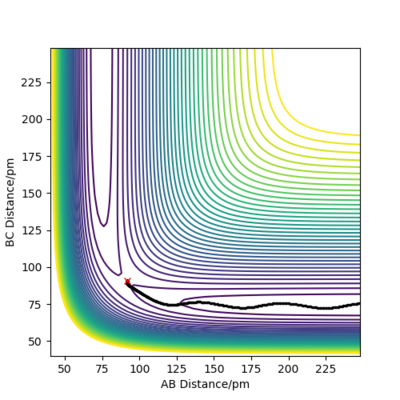
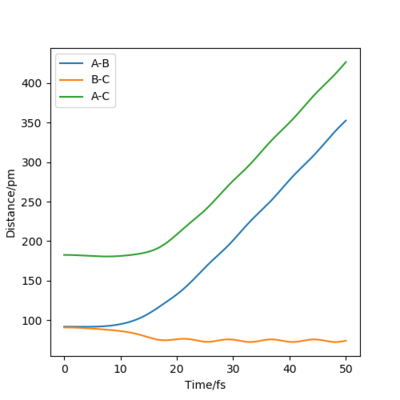
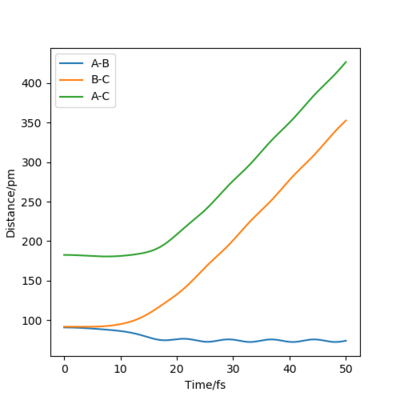
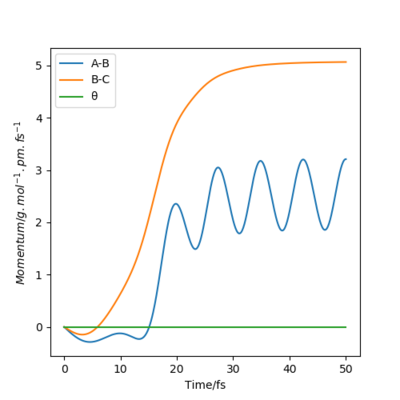
Question 5
Setup a calculation where the initial positions correspond to the final positions of the trajectory you calculated above, the same final momenta values but with their signs reversed. What do you observe?
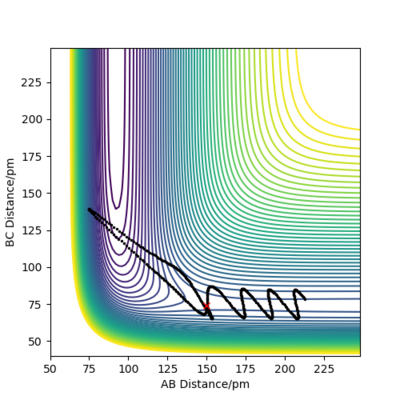
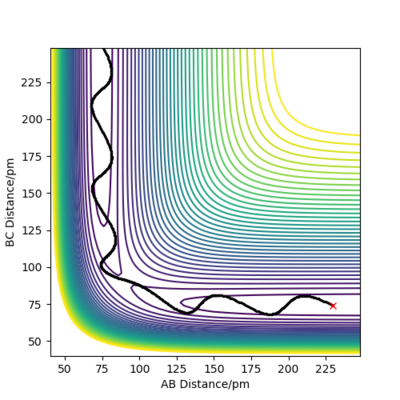
Varying the sign of momenta has a dramatic effect on wether a reaction occurs. For 2 positive values of momenta, the atom and molecule will never collide and will in fact move further apart from each other, whereas with both negative signs, the atom and molecule (A and B-C) will eventually collide and for A-B and C as shown by Figure 12. The fact that the two atoms collide is due to the fact that the atom will have a much greater velocity than the molecule.
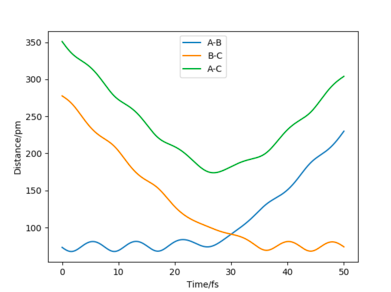
Question 6
Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?
This tables is a summary of reactive and unreactive trajectories of a H-H-H system with varying values of momenta, where rA-B=230pm and rB-C =74pm.
| p1/ g.mol-1.pm.fs-1 | p2/ g.mol-1.pm.fs-1 | Etot (kJ.mol-1) | Reactive? | Description of the dynamics | Illustration of the trajectory |
|---|---|---|---|---|---|
| -2.56 | -5.1 | -414.280 | Yes | Molecule of BC is approached by atom A. A bonds to B and the BC bond breaks and C moves away, with small oscillators. Reactants have enough energy to pass over the transition sate so when A Collides with BC, AB is formed. |  
|
| -3.1 | -4.1 | -420.077 | No | Atom A moves towards B-C, where the bond is oscillating and then A moves away from B-C. This trajectory tells us that A did not have enough energy to overcome the transition barrier and therefore no reaction occurs. |  
|
| -3.1 | -5.1 | -413.977 | Yes | A approaches B-C and collides, B-C bond has very small oscillations. New A-B bond is formed, which oscillates at a higher amplitude. A-B and C move apart in opposite directions with C having a higher velocity. As A has a high initial velocity and B-C molecule is also moving towards A at a lower velocity, the system has enough energy to overcome the activation barrier and react. |  
|
| -5.1 | -10.1 | -357.277 | No | Atom A and molecule B-C have large oscillations. As A approaches B-C it bonds to B and B-C bond is broken and C moves away a small amount but then moves back towards B and reforms the B-C bond, then A moves away. As reactant have alot of energy and are moving at high velocities the energy barrier is easily overcome so the forward reaction proceeds, however, as there energy is so high when B and C meet after dissociation the have enough energy to overcome the reverse reaction energy barrier, so the backwards reaction occurs. |  
|
| -5.1 | -10.6 | -349.477 | Yes | A approaches B-C molecule and collides to form A-B molecule and C moves away. C then moves back towards A-B molecule and reforms the transition state. C then moves further away as A-B oscillates. The energy of the reactants are is sufficient to overcome the transition state barrier, as a result, the reactants collide successfully to form the products |  
|
In conclusion, from this table we can deduce that reactants must have energy greater the the transition barrier for the reaction to take place. Too little energy and the scenario where Etotal=-420.077KJmol-1 will occur where no reaction will take place. Too much energy and there is the potential that the backwards reaction may be forced after the forward reaction has taken place e.g. where Etotal= -357.277KJmol-1.
Good table layout and conclusion. Your conclusion would be better if you account for the cases that don't fit with your statement, ie your final sentence states that "the backwards reaction may be forced..." but this is not the case for the final reaction listed in your table above Sf3014 (talk) 11:07, 2 June 2020 (BST)
Question 7
Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
Transition state theory makes several assumptions which cause its value to differ from the experimental values. It assumes that all trajectories with a kinetic energy along the reaction coordinate greater than the activation energy will react.[3] It also assumes that kinetic energy follows a Boltzmann distribution along reaction coordinates. Motion of system over the transition state barrier is considered classically.
Finally, the Transition state theory does not account for Quantum tunnelling, whereby it is possible for particles to tunnel across transition state barrier at a lower energy, thus increasing rate of reaction.
Your conclusion on how transition state theory (TST) will affect the rate compared to the experimental rate is unclear because you gave examples which will have different affects on the rate of the reaction compared to the experimental rate. Also, use examples from your table to aid your description Sf3014 (talk) 00:08, 2 June 2020 (BST)
EXERCISE 2: F - H - H system
Question 1
By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
In exothermic reactions, energy is released when bonds are formed in the products, which is greater than energy of bond breaking in reactants. This release of energy is often characterised by increase in thermal energy of the system. On the other-hand, if a system is absorbing energy, where more energy is required to form bonds than break them, the reaction is said to be exothermic. The F + H2 reaction is exothermic as a formation of a H-F is energetically much more favourable due to large difference in electronegativity resulting in strong electrostatic interactions and a stronger bond. From this, we know that the H-H bond requires much less energy to break than the gain in energy from the formation of a H-F bond. The H + HF reaction is endothermic for the opposite reasons, as large amount of energy is required to break the H-F bond and the net gain in energy is small from formation of H-H bond. In conclusion, the H-H bond strength is much weaker than the H-F bond
Good expect small error in your description for endothermic reactions, you wrote exothermic. You need to refer to your potential energy plot in your description and explain how the plot shows this clearly. Also, some published experimental values for the bond energies would aid your description Sf3014 (talk) 11:15, 2 June 2020 (BST)
Question 2
Locate the approximate position of the transition state.
For the H-F bond the transition state was determined to be 181.8pm and for H-H it was determined to be 74pm. In both these cases the central H atom is bonding to F and H respectively with minimal bond vibrations. As we know that the F + H2 reaction is exothermic, from the Hammond’s postulate we know that the transition state will ressemble the reactants, whereas for H +HF, which is an endothermic reaction, it will resemble the product, H2. This is the reason that in Figure 13 the reaction pathway for formation of H-F has a lower potential energy that formation of H2.
Good but more information is needed on how you got to these distance for your transition state. Where did you get the information on Hammond's postulate? Reference. Also, where in figure 13? When you mentioned the minimal bond vibrations you could of referred to figure 2. Also, your figure numbers are confusing, you can have two figures 2's on one report if you want to label them by section you can label that figure 1.2 and 2.2 for sections 1 and 2, respectively Sf3014 (talk) 11:21, 2 June 2020 (BST)
Question 3
Report the activation energy for both reactions.
To determine the activation energy for each of the reactions an MEP calculation starting with a small displacement from the transition state was run with a larger number of steps so that the potential energy converges on a value. From this energies at different states were determined to be H-F = -560.700 kJmol-1, H-H = -434.183 kJmol-1 and Transition state= -433.70 kJ.mol-1. Using this data, the activation energy for F+H2 system was calculated at 1.13KJmol-1 and for the H+HF system it was determined to be 127KJmol-1, the activation energy of the second system is much larger due to the reaction being endothermic.
Good but you could be clearer, you have given numbers and said you calculated something but the calculation is not clear. You can state that you found out the differences in the energies or show difference using the energy time graph. The latter would be more beneficial because your starting statement describes this Sf3014 (talk) 11:35, 2 June 2020 (BST)
Question 4
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.
For the exothermic reaction F+H2, there is an early transition state, whereby, the energy is generated from the exothermic reaction is released into vibrational energy of HF, due to attractive release of energy of H-F molecule formation. This vibration of the bond can be observed experimentally.[4]
Good but what shows that the energy is converted into vibrational energy? Use your evidence (with proper reference) from your simulations and describe it. And how can this be measured experimentally? Sf3014 (talk) 11:41, 2 June 2020 (BST)
Question 5
Setup a calculation starting on the side of the reactants of F + H2, at the bottom of the well rHH = 74 pm, with a momentum pFH = -1.0 g.mol-1.pm.fs-1, and explore several values of pHH in the range -6.1 to 6.1 g.mol-1.pm.fs-1 (explore values also close to these limits). What do you observe?
| p1/ g.mol-1.pm.fs-1 | p2/ g.mol-1.pm.fs-1 | observations | Figure showing the trajectories of the molecule |
|---|---|---|---|
| -6.1 | -1.0 | H-H reacts with the F to form H-F, however as the system is very high energy, greater than the transition barrier for forwards and backwards reactions, an equilibrium is established between the forwards and backwards reactions. | 
|
| -5.0 | -1.0 | F reacts with H-H to form H-F and F, the system has enough energy to overcome the transition barrier and for forwards and backwards reactions, after the backwards reaction occurs and H-H is reformed, the system does not have enough energy to form H-F again | 
|
| -1.0 | -1.0 | System has enough energy to overcome the transition barrier and form HF | 
|
| 0 | -1.0 | System has enough energy to overcome the transition barrier and form HF | 
|
| 2 | -1.0 | System has sufficient energy to overcome transition barrier. Therefore, F atom successfully reacts with H-H to form H-F and H atom | . 
|
| 6.1 | -1.0 | F reacts with H-H to form H-F and H. System is high energy and as a result there is sufficient energy to overcome that reverse reaction activation barrier. An equilibrium is established between reactants and products | 
|
From the table above, we can deduce that when a system has high energy greater than the transition barrier, due to conservation of energy, this barrier can be crossed at any point, which establishes an equilibrium. At lower energy, where the atom and molecule have lower momenta, the system will just favour the forward reaction as it doesn't have enough energy to overcome the backwards transition barrier.
Good table layout. More clarity gained if p1 and p2 was labelled pHH and PHF in the table. Also, give examples in your conclusion Sf3014 (talk) 11:46, 2 June 2020 (BST)
Question 6
For the same initial position, increase slightly the momentum pFH = -1.6 g.mol-1.pm.fs-1, and considerably reduce the overall energy of the system by reducing the momentum pHH = 0.2 g.mol-1pmfs-1. What do you observe now?
In this modified system, the total energy of the system has decreased. F atom approaches H-H and reacts to form H-F and H atom, as there is sufficient energy to overcome the forward transition barrier, however the system doesn't have enough energy to overcome the backwards transition barrier to reform H-H.
What energies are you talking about? Explanation is spread too wide your point is loss Sf3014 (talk) 11:51, 2 June 2020 (BST)
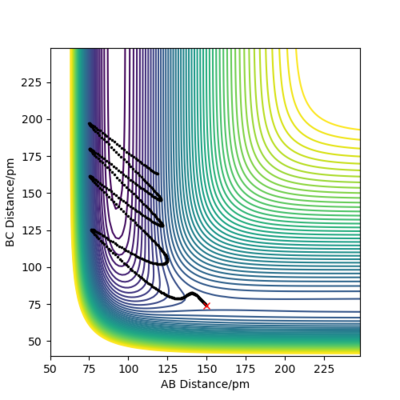
Question 7
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
To answer this question we must consider Polanyi's empirical rules. It states that vibrational energy is more efficient than translational energy in activating a late-barrier reaction, whereas the reverse is true for an early-barrier reaction.[4] From this we can determine how the location of transition barrier affects system energy requirements for reaction to occur. When considering the exothermic reaction of F+HH this transition barrier is the entrance to the lowest points of the PES graph and therefore can be described as an early-barrier, therefore, translational energy is more efficient than vibrational energy for promoting the reaction, more efficient reaction. On the other hand for the endothermic reaction of H+HF, this reaction is reversed and therefore has a late-barrier, so vibrational energy is more efficient than translational energy for promoting the reaction.
Good but refer to the evidence from the simulations above, your analysis of the vibrational (molecule momenta) and the translational (atom momenta) energies Sf3014 (talk) 11:55, 2 June 2020 (BST)
references
- ↑ 1.0 1.1 http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year1/6_freq_analysis_theory.html
- ↑ 2.0 2.1 heoret. Chim. Acta (Bed.) 66, 245-260 (1984) p
- ↑ 3.0 3.1 https://wiki.ch.ic.ac.uk/wiki/index.php?title=CP3MD
- ↑ 4.0 4.1 4.2 https://www.chemistryviews.org/details/news/1378289/New_Rules_for_Reaction_Dynamics.html