MRD:CMB01333464Y2

EXERCISE 1: H + H2 system

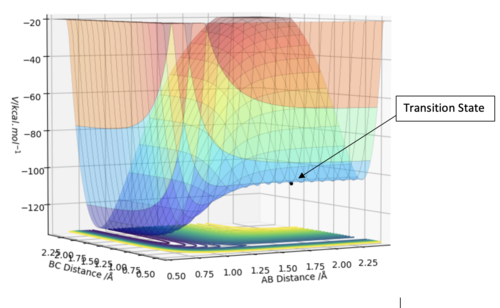
Transition State

How is the transition state mathematically defined?

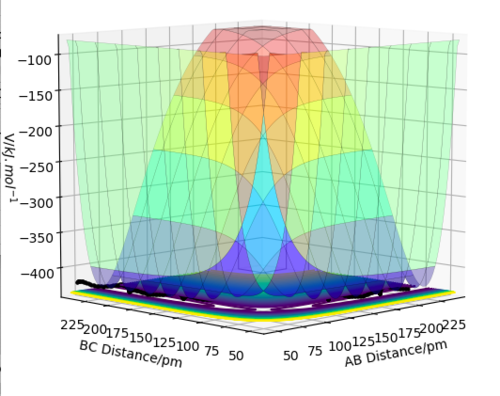
The transition state is defined as the maximum point on the minimum energy path linking the reactants and the products. This can be mathematically defined as a saddle point and we can determine these points by taking the partial derivative with respect to both q₁ and q₂ and finding the point where these are both equal to 0, $\frac{\partial V}{\partial q_{1}} = \frac{\partial V}{\partial q_{2}} = 0$ , where V is the potential energy of the system and q₁ is a normalised vector the tangent to the reaction pathway and q₂ is a normalised vector orthogonal to the reaction pathway thus defining a new set of orthogonal basis vectors for a new coordinate system. We then require there to be a maximum along q₁ and a minimum along q₂ which are characterised by the conditions that $\frac{\partial^{2} V}{\partial q_{1}^{2}} < 0$ and $\frac{\partial^{2} V}{\partial q_{2}^{2}} > 0$ ^[1] How do the second derivatives compare for a local minimum? Pu12 (talk) 15:23, 23 May 2019 (BST)

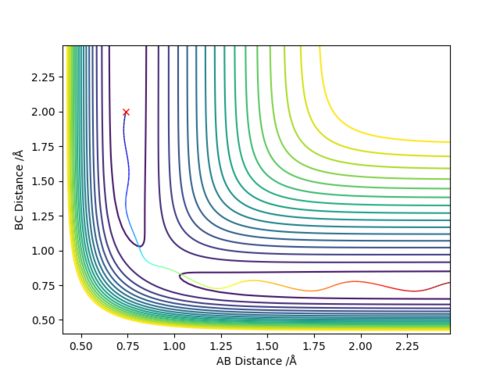
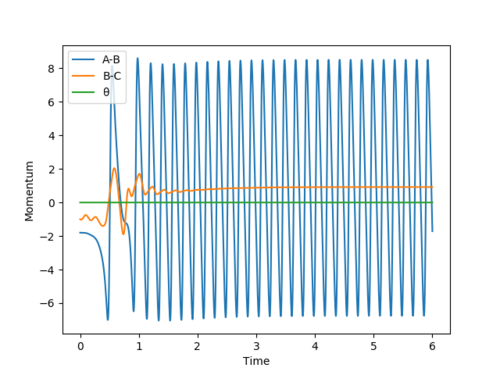
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

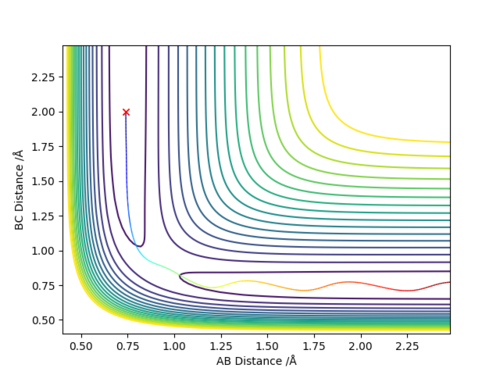
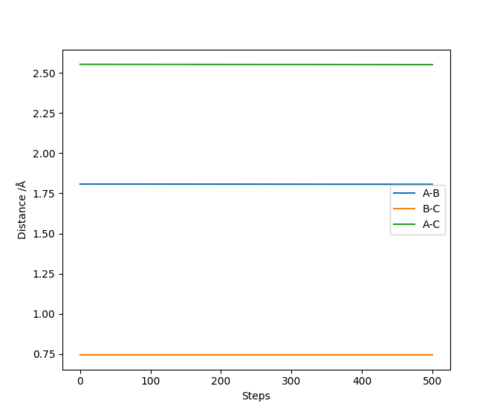
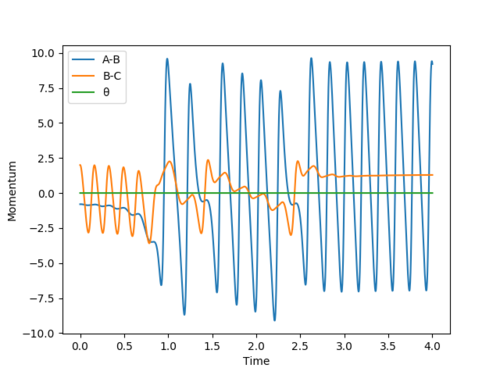
We can find the value for the transition state position using the Internuclear Distance vs Time graph. By setting r₁ = r₂ and giving no initial momentum we can see that there are oscillations corresponding to the reaction pathway oscillating in a potential well on the ridge of the saddle point where the transition state position will be at the average of the minimum and maximum values of the oscillation for the the A-B and B-C distances. By doing this we can get an approximate value for the transition state and then iterating our value into a new set of initial conditions until we have a flat line for the plot. By using this method we find the transition state position to be approximately 0.908 Å Good. Pu12 (talk) 15:23, 23 May 2019 (BST)

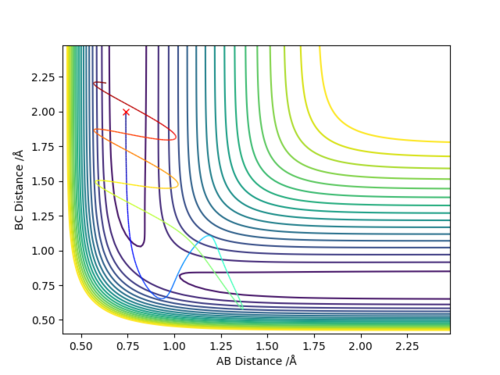
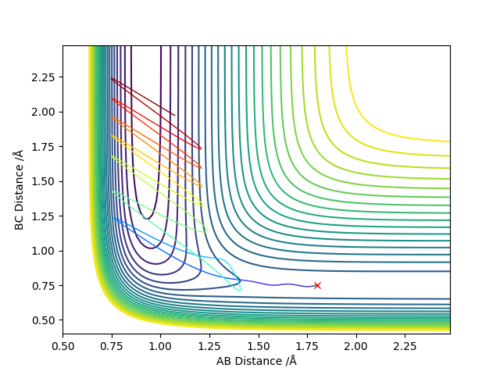
Comment on how the mep and the trajectory you just calculated differ.

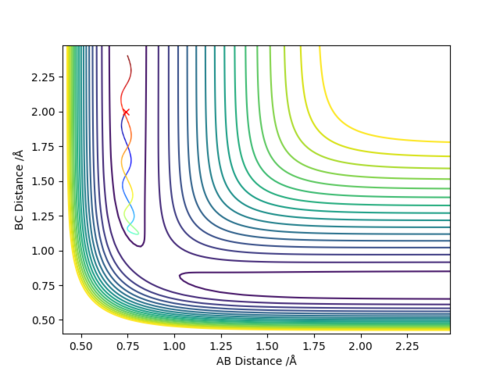
There are two main differences in the MEP and dynamics trajectory, firstly you can see that the length of the dynamics trajectory is longer than that of the MEP trajectory and secondly the MEP trajectory is very smooth and linear whereas the dynamics trajectory has oscillations. Both of these difference can be accounted for by the fact that in the MEP trajectory for every time step the reaction pathway moves along the direction of steepest descent by an amount proportional to the magnitude of the gradient and then resets the momenta/velocities back to zero so in moving from one point to another there is no gain in energy. This is why you see the smooth linear pathway for the MEP pathway which always moves in the direction of steepest descent and then once it gets to the flat region it stops as the gradient is now equal to 0 and so there is no extra movement. However in the dynamics pathway where it better represents realistic motion, the atoms have mass and hence carry momenta and will have inertia and a tendency to continue moving in a straight line until that state is changed by an external force and so don't follow exactly the pathway of steepest descent for every time step but continue to move up the potential energy surface until the kinetic energy has been transferred into potential energy and then will move back down the potential surface and carry on which is observed in the oscillations that we see and the fact that the pathway does not simply stop like that of the MEP.

Reactive and unreactive trajectories


P1	P2	E_tot	Reactive?	Description of the dynamics
-1.25	-2.5	-99.018	Yes	Case1: The reaction H_A-H_B + H_C -> H_B-H_C + H_A proceeds. H_A-H_B has little vibrational energy and collides with H_C overcoming the transition barrier and forming the product H_B-H_C with some vibrational energy while H_A is ejected.
-1.5	-2.0	-100.456	No	Case2: The reaction H_A-H_B + H_C -> H_B-H_C + H_A does not proceed. H_A-H_B collides with H_C however does not have enough total energy to overcome the transition barrier and so H_A-H_B and H_C fall away from one another.
-1.5	-2.5	-98.956	Yes	Case3: The reaction H_A-H_B + H_C -> H_B-H_C + H_A proceeds. H_A-H_B has little vibrational energy and collides with H_C overcoming a transition barrier and forming the product H_B-H_C with some vibrational energy while H_A is ejected.
-2.5	-5.0	-84.956	No	Case4: The reaction H_A-H_B + H_C -> H_B-H_C + H_A does not proceed. H_A-H_B collides with H_C with a high total energy overcoming the transition barrier and starts to form the product H_B-H_C with high vibrational energy which then passes back over the transition barrier forming the reactants again where H_A-H_B has a high vibrational energy and move away from one another.
-2.5	-5.2	-83.416	Yes	Case5: The reaction H_A-H_B + H_C -> H_B-H_C + H_A proceeds. H_A-H_B collides with H_C with a high total energy overcoming the transition barrier and starts to form the product H_B-H_C with high vibrational energy which then passes back over the transition barrier forming the reactants again and then recrosses the barrier a second time forming H_B-H_C and H_A with a high vibrational energy and move away from one another.

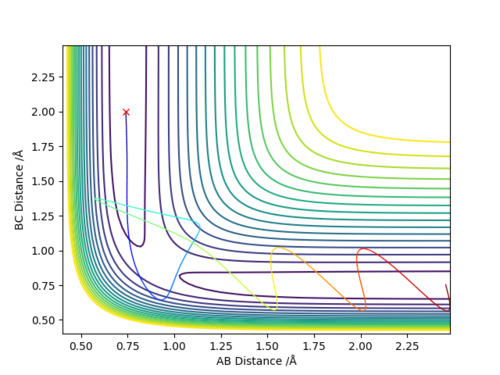
Before we would of assumed that trajectories starting from the same position with higher kinetic energies would of easily overcome the transition state and a reaction would of taken place however from the table it is clear that having sufficient energy is not the only factor for a reaction to take place as we can see that even though in case 4 there is more total energy the reaction does not proceed compared to case 1 with a lower total energy going into the collisions. The other key factor that has to be taken into account is that the vibrational state of the molecule has to be correct for the reaction to take place. Good. Pu12 (talk) 15:23, 23 May 2019 (BST)

Assumptions of Transition state theory

When applying transition state theory to potential energy surfaces we make the assumptions,

1. Quantum tunnelling effects are assumed to be negligible and the Born-Oppenheimer approximation is invoked.

2. Once the system has gone over the transition state towards the product then it cannot return back.

3. The reactants are in thermal equilibrium with the activated complex.

4. The atoms in the reactant state have energies that are Boltzmann distributed and this should be satisfied is the system has had enough time to thermally equilibrate. ^[2]

If we look at the trajectories tested in the table then one would expect that the transition state theory would predict the reaction rates to be faster than that of the experimental values obtained because if we were assuming theory then the system recrossing the barrier could not take place and thus once the barrier had been cross then given that the reaction has sufficient energy in the first place then it would proceed whereas a portion of reactions would not go through in the experiments due to not having the right vibrational state and thus lowering the reaction rate.

Good. Pu12 (talk) 15:23, 23 May 2019 (BST)

EXERCISE 2: F - H - H system

PES inspection

By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

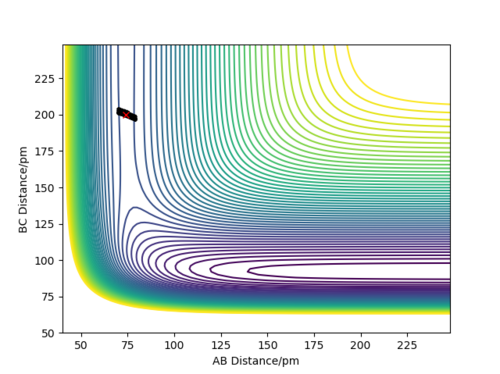
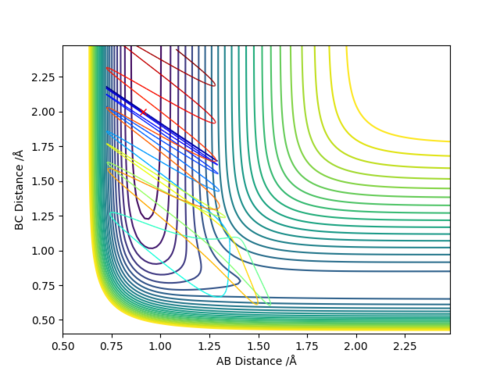
We can plot the potential energy surface plot for the reaction of F and H₂ and using this plot we can see that the reactants (F and H₂) on the right side of the plot with a larger value for AB and a short value of BC are higher in energy than the products (H and HF) on the left. This is telling us that the reaction for F + H₂ -> H + HF is exothermic as the reactants are higher in energy than the products thus the reaction gives energy out and therefore for the reverse reaction H + HF -> F + H₂ -> H + HF is endothermic as the reactants are lower in energy than the products and thus the reaction takes energy in.


Reaction	Exothermic or Endothermic
F + H₂ -> H + HF	Exothermic
H + HF -> F + H₂	Endothermic

From this we can conclude that the bond strength of the HF bond is stronger than that of the H₂ bond because the reaction F + H₂ -> H + HF is exothermic meaning that more energy is released from the HF bond forming than the energy put in the break the H₂ bond and similarly for the reverse reaction H + HF -> F + H₂ -> H + HF is endothermic meaning that more energy was required to break the HF bond than was released from the formation of the H₂ bond.

Locate the approximate position of the transition state

To locate the approximate energy of the transition state we can use Hammonds postulate on the reaction H₂ + F -> HF + H to conclude that because the reaction is exothermic then we can say that the transition state is going to resemble the reactants more than the products and so we can use an MEP trajectory along the valley of the reactants pathway to try and find an approximate value for the transition state and then back up out value using the internuclear distance versus time plot.


Transition state location
HF Bond length 1.808 Å and HH Bond length 0.745 Å

Report the activation energy for both reactions

In order to calculate the activation energy for both of the reactions we require the difference in values of the reactants and the transition state and the products and the transition state. Because we know approximately where the transition state is we can slightly offset the position of the MEP trajectory from the transition state for it to fall into the products or reactants and then look at the Energy versus Time plot to find a difference in energy.


Reaction	Energy Vs Time plot	Activation energy
F + H₂ -> HF + F		0.2
HF + F -> F + H₂		30.2

Reaction Dynamics

In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.

F + H₂ -> HF + H

We can see from looking at the animation, Momentum v Time plot and the Contour plot that the HF molecule after the reaction has a lot of excess vibrational energy and thus we can suggest that the release of energy from this reaction is from translation energy prior to the collision and then transferred to vibrational energy via the vibrating HF molecule. This could be confined experimentally using techniques such as bomb calorimetry to measure the change in temperature that would occur due to the excess vibrational energy transferring energy to surrounding molecules to heat up the surrounding environment and thus the energy change or potentially IR spectroscopy to see the emissions from the excited molecule. Good, but please note that energy release isn't just translational -> vibrational but also potential -> vibrational. Pu12 (talk) 15:23, 23 May 2019 (BST)

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

The reaction F + H₂ -> HF + H was investigated using a constant value of the translation energy going into the reaction of -0.5 and varying the vibrational energy between the H₂ molecule with initial conditions of rH_AH_B = 0.74 and rH_BF = 2.0. Below is a table of the findings and we can see that even though the energy put into the vibrational energy of the H₂ bond is larger than the activation energy for the reaction to proceed that it is not guaranteed to proceed and in most cases it doesn't however there are some regions where the reaction seems to proceed and regions where it does not proceed.


pH_A-H_B	Proceed or not
-3.0	No
-2.0	No
-2.5	No
-2.0	Yes
-1.5	Yes
-1.0	Yes
-0.5	Yes
0.0	Yes
0.1	No
0.5	No
1.0	No
1.5	No
2.0	No
2.5	No
2.85	Yes
2.9	Yes
2.95	Yes
3.0	No

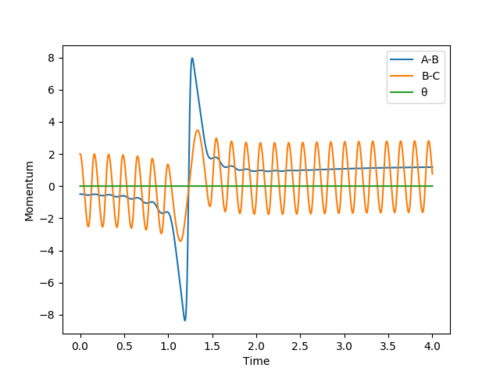
However if we were to increase the translation energy of the reaction to -0.8 then the reaction is now successful. Below we can see below from the Momenta vs Time plots of the reaction with translation energies at -0.5 (on the left) and -0.8 (on the right) we can see that the reaction becomes successful after a small increase in the translational energy.

This can be explained by Polanyis rules that state for an exothermic reaction where the transition state is early then the reaction is more dependent on the translational energy compared to the vibrational energy. This is in agreement with the rules as before when we had little translational energy and as we varied that vibrational energy then there was little effect on whether the reaction would proceed or not then once we increased the kinetic energy to -0.8 we can see that the reaction proceeds because of the fact that the reaction efficiency is mostly dependent on the translational energy.^[3] Good. Pu12 (talk) 15:23, 23 May 2019 (BST)

If we look at the reverse reaction H + HF -> F + H₂ we know that it is an endothermic reaction and so Polanyis rules state that for an reaction with a late transition state such as an endothermic reaction the efficiency of the reaction will depend on the vibrational contribution more so than the translational contribution. The first figure on the left is for initial conditions of rHF = 0.913 and rHH = 2 with pHF = -9 and pHH = -0.01 and the figure on the right with initial conditions rHF = 0.913 and rHH = 2 with pHF = -9 and pHH = -10. For both of these reactions they do not proceed and this shows that for a fixed value of vibrational energy and varying the translation energy by a large amount that the reaction still does not proceed even thought the total energy is more than that for the activation energy of the reaction. However when we change the vibrational energy of the HF bond by 1 then the reaction proceeds as we can see in the bottom figure and this agrees with Polanyis rules because it is an endothermic reaction with a late transition state and so we can see it is more dependent on the vibrational energy of the HF bond compared to the translation energy.

This is a good report with very few corrections to make 5/5 well done. Pu12 (talk) 15:23, 23 May 2019 (BST)

References

↑ Peter Atkins and Julio de Paula, Physical Chemistry (8th ed., W.H. Freeman 2006), p.809 ISBN 0-7167-8759-8
↑ Anslyn, Eric V.; Doughtery, Dennis A., Transition State Theory and Related Topics. In Modern Physical Organic Chemistry University Science Books: 2006; pp 365–373
↑ Jiang, B. and Guo, H., 2013. Relative efficacy of vibrational vs. translational excitation in promoting atom-diatom reactivity: Rigorous examination of Polanyi's rules and proposition of sudden vector projection (SVP) model. The Journal of chemical physics, 138(23), p.234104.

[[1]-1] Peter Atkins and Julio de Paula, Physical Chemistry (8th ed., W.H. Freeman 2006), p.809 ISBN 0-7167-8759-8

[[2]-2] Anslyn, Eric V.; Doughtery, Dennis A., Transition State Theory and Related Topics. In Modern Physical Organic Chemistry University Science Books: 2006; pp 365–373

[[3]-3] Jiang, B. and Guo, H., 2013. Relative efficacy of vibrational vs. translational excitation in promoting atom-diatom reactivity: Rigorous examination of Polanyi's rules and proposition of sudden vector projection (SVP) model. The Journal of chemical physics, 138(23), p.234104.

[1]

[2]

[3]