MRD:CH1516
Exercise 1
Q: What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
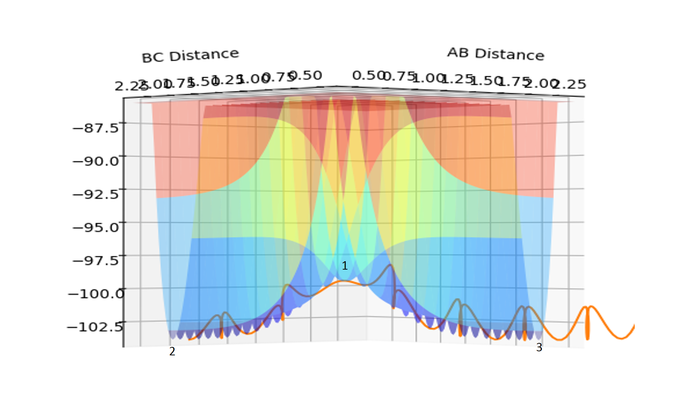
A: r1 = distance of H1-H2; r2 = distance of H2-H3
There are two minima and one transition structure. Point 1 is the transition state, while point 2 and point 3 are minima. Because they are all stationary points, their first derivatives are always zero. The difference lies in the second derivatives.
For a minimum, both ∂2V/∂r12 and ∂2V/∂r22 are larger than 0, while for a transition structure, ∂2V/∂r12 > 0, and ∂2V/∂r22 < 0.
(Almost perfect. At the TS, the second-order partial derivates have opposite signs along the reaction coordinate and its orthogonal coordinate. Fjs113 (talk) 21:36, 10 May 2018 (BST))
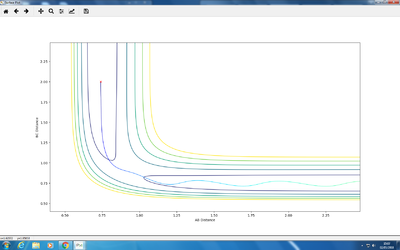
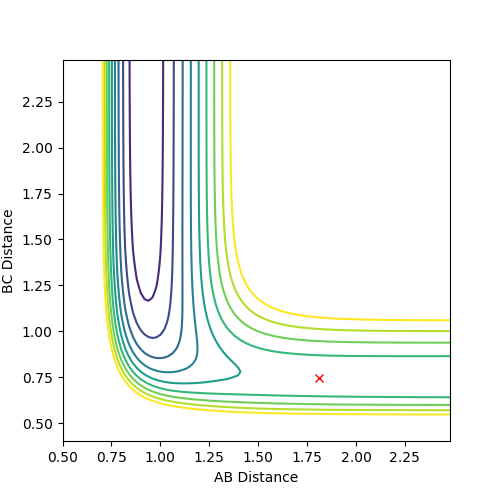
Q: Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
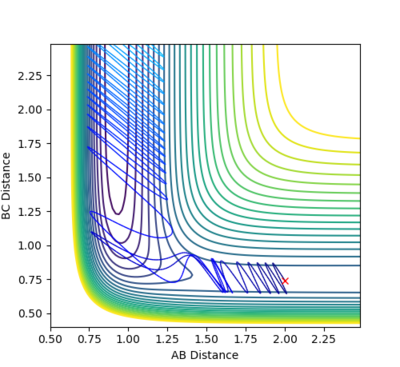
A: Steps = 830; Cutoff = -77 Kcal/mol. My best estimate of transition structure in this situation is AB distance = BC distance = 0.91202188.
The distance is chosen because as shown in the graph, the point does not roll down and is stay at a stationary point region. The reason why it does not roll down, after 830 steps, must because it does not experience a net force. Therefore, the force on it is zero. Also, force is the gradient of the potential energy diagram, so it can be concluded that the gradient at that point is also zero. Therefore, it is a stationary point, and also the transition state.
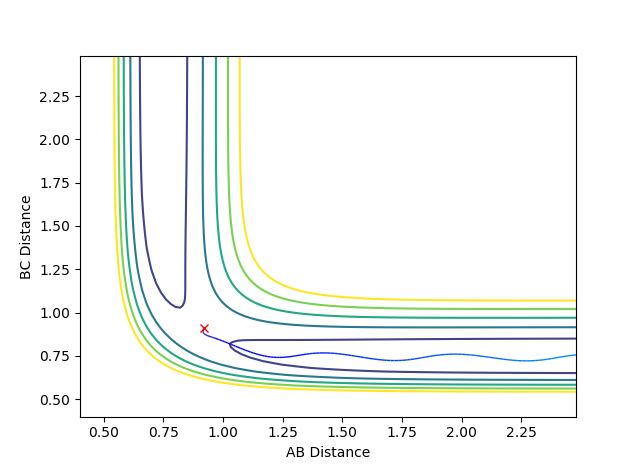
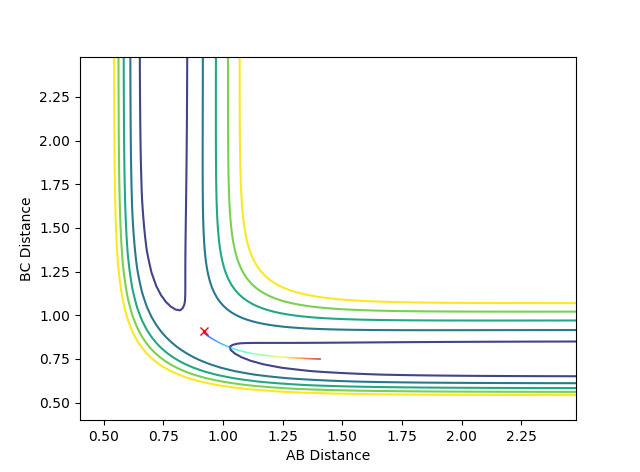
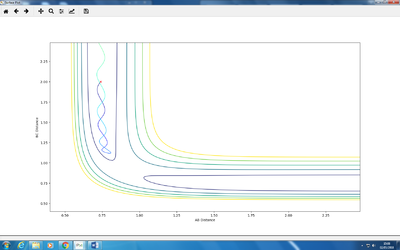
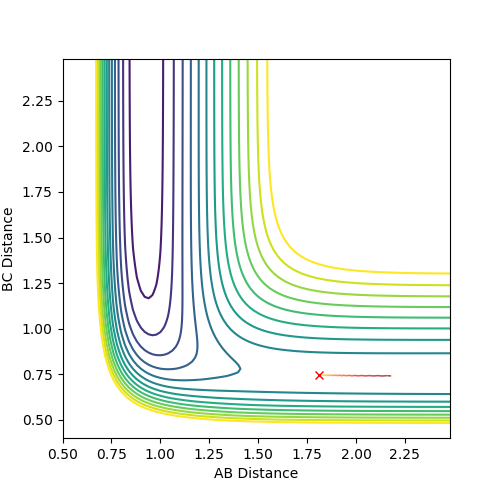
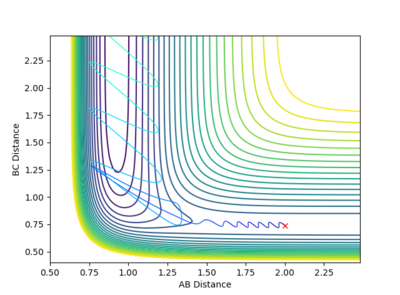
Q: Comment on how the mep and the trajectory you just calculated differ.
The trajectory under dynamics condition
The trajectory under MEP condition
Firstly, the dynamics trajectory goes through a long journey while MEP only moves through a small distance. This is because is the MEP condition, the velocity at any moment is reset to zero, hence the velocity would not be accumulated. In other words, the inertia is removed. Secondly, the dynamics trajectory is wavey. This is because while move through the potential surface, the molecule is still vibrating and the wave is due to the change in bond length from vibration. However, there is no vibration is MEP because of the same reason: once the equilibrium is reached, there is no velocity in the system and the molecule simply could not vibrate anymore and just stays at the equilibrium position.
(Very good! Fjs113 (talk) 21:36, 10 May 2018 (BST))
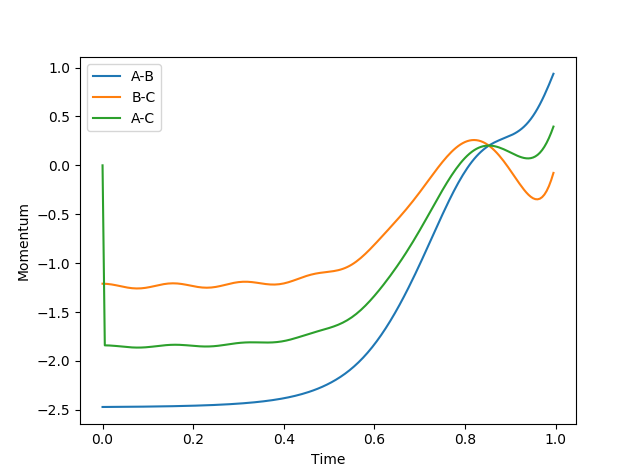
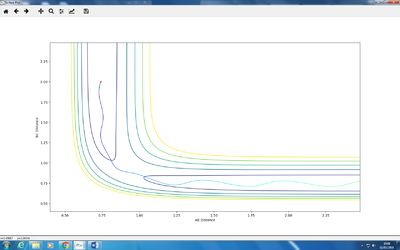
Q: Look at the “Internuclear Distances vs Time” and “Internuclear Momenta vs Time”. Take note of the final values of the positions r1(t) r2(t) and the average momenta p1(t) p2(t) at large t.
What would change if we used the initial conditions r1 = rts and r2 = rts+0.01 instead?
A: when steps = 200, and r1 = rts + 0.1
| final distance | final momentum | |
|---|---|---|
| A-B | 3.44 | 2.47 |
| B-C | 0.74 | 1.21 |
| A-C | 4.14 | 1.85 |
when r2 = rts + 0.1
| final distance | final momentum | |
|---|---|---|
| A-B | 0.74 | 1.21 |
| B-C | 3.44 | 2.47 |
| A-C | 4.14 | 1.85 |
When r2 is increased instead, the second situation just simply a reverse of the first situation - A-B forms the molecule instead of B-C. The final momentum is reversed too.
(A few plots would've illustrated this better. Fjs113 (talk) 21:36, 10 May 2018 (BST))
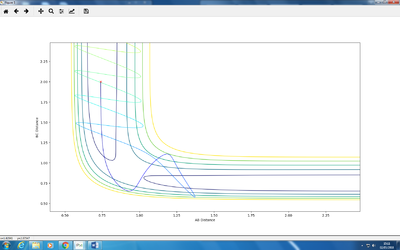
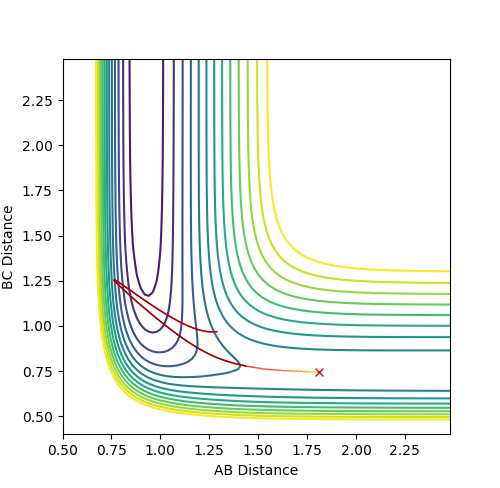
Q: Setup a calculation where the initial positions correspond to the final positions of the trajectory you calculated above, the same final momenta values but with their signs reversed.
A:
As can be seen, there momentum would cross off at around 0 at some time simultaneously!
(What are the initial conditions used to obtain this? And what does the plot mean? We're looking for an explanation here. Fjs113 (talk) 21:36, 10 May 2018 (BST))
Q: Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.
A:
| set | p1 | p2 | energy | reactive? |
|---|---|---|---|---|
| 1 | -1.25 | -2.5 | -98.6 | Yes |
| 2 | -1.5 | -2.0 | -100.1 | No |
| 3 | -1.5 | -2.5 | -98.75 | Yes |
| 4 | -2.5 | -5.0 | -84.8 | No |
| 5 | -2.5 | -5.2 | -83.0 | Yes |
Set1
Description: This is a reactive system. C approaches A-B while A-B is not vibrating, then B and C formed a molecule, and moves away from A while vibrating.
Set2
Description: This is an unreactive system. C approaches A-B while A-B is vibrating, then C collides with A-B but does not have enough energy to overcome the energy barrier and react. Therefore, C is bounced off and moves in another direction.
Set3
Description: This is a reactive system. C approaches A-B while A-B is vibrating, then B and C formed a molecule, and moves away from A while vibrating. The difference from set 1 is the initial state of A-B.
Set4
Description: This is an unreactive system. C approaches A-B while A-B is not vibrating, then C collides with A-B and crosses the energy barrier. However, the system then crosses back the barrier and regenerates the reactants. Therefore, C is bounced off and moves in another direction in a slow speed. A-B is collided and starts to vibrate violently
Set5
Description: This is a reactive system. C approaches A-B at a fast speed, then C collides with A-B and crosses the energy barrier. However, the system then crosses back the barrier and regenerates the reactants. Therefore, C is bounced off and moves in another direction in a slow speed.
Q: State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
A: Main assumptions:
1. reactant molecules are distributed among their states in accordance with Boltzmann distribution. 2. Molecular systems that have crossed the trasition state in the direction of products cannot turn around and reform reactants. 3. In the transition state, motion along the reaction coordinate may be separated from the other motions and treated classically as a translation.
In the case of set 4 and set 5, transition state theory deviates from reality, and it over-estimate the rate of the reaction
(Please give some justification for this claim. Fjs113 (talk) 21:36, 10 May 2018 (BST))
Exercise 2
In this exercise, A = F, B = H and C = H
Q: Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
A: The F + H2 reaction is exothermic and the H + HF is endothermic as can be seen in the diagram.
(How is this seen in the diagram? You need to explain the difference in the depth on the PES and relate that to exo/endothermic. Fjs113 (talk) 21:36, 10 May 2018 (BST))
The bond energy of H-H is 435 kJ/mol; the bond energy of H-F is 569 kJ/mol. Forming H-F would be exothermic.
(Where did these values come from? -> Reference. Fjs113 (talk) 21:36, 10 May 2018 (BST))
Q: Locate the approximate position of the transition state.
A: Steps = 4000; Cutoff = -86 Kcal/mol; A = F, B = H, C = H At transition state; AB distance = 1.8112 A; BC distance = 0.7440 A; AB momentum = BC momentum = 0
(Good. Would've been even better if you gave some justification/derivation. Fjs113 (talk) 21:36, 10 May 2018 (BST))
As can be seen form the graph, the system does not fall down the potential surface under dynamics condition after 1300 steps. This means it is at a transition state, as followed from the same argument from exercise 1.
To confirm that this is a transition state, the distances are slightly changed. When the A-B is increased from 1.8112 to 1.8113, the system rolls down to the left, while when the A-B is decreased to the 1.8111, the system rolls down to the right. This is an indication of transition state because if it is a minimum, the system will quickly revert back to the minimum, rather than rolling all the way down to two directions.
Q: Report the activation energy for both reactions.
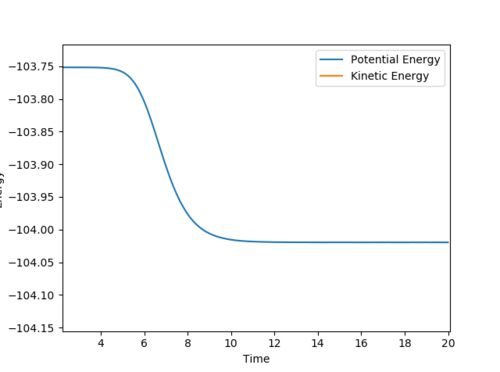
A: The system is slightly displaced from equilibrium position to A-B = 1.8113. This is because I want it to roll down the hill from F-H-H transition state to F and H2 reactants, hence I can locate the energy of the transition state and the reactant. The potential energy vs. time is shown below.
As can be seen, because the system is only slightly displaced (from 1.8112 to 1.8113) from transition state, so where it starts is basically the energy of transition state, which is -103.75 kCal/mol to two decimal place. The reactants (F and H2) energy can also be read at -104.02 kCal/mol. The activation energy from F and H2 direction is hence 0.27 kCal/mol.
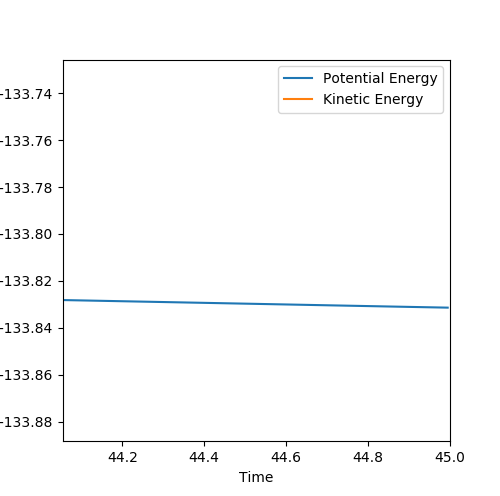
To determine the reactant energy of H and H-F, the initial distance of H-F is set at 1.1, which then rolls down the hill to the H and H-F side, and hence the potential energy could be read off. The graph is shown below.
It can be easily seen that the reactant energy is -133.83 kCal/mol, hence the activation energy from H and H-F side is 30.07 kCal/mol, which is much larger than the other direction.
(Good explanation. Fjs113 (talk) 21:36, 10 May 2018 (BST))
Q: Setup a calculation starting on the side of the reactants of F + H2, at the bottom of the well rHH = 0.74, with a momentum pFH = -0.5, and explore several values of pHH in the range -3 to 3 (explore values also close to these limits). What do you observe? Note that we are putting a significant amount of energy (much more than the activation energy) into the system on the H - H vibration.
A:
| pHH value | picture | reactive? | pHH value | picture | reactive? |
|---|---|---|---|---|---|
| 1.9 | 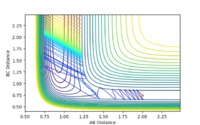 |
yes | -1.9 |  |
yes |
| 2.0 | 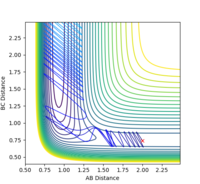 |
yes | -2.0 | 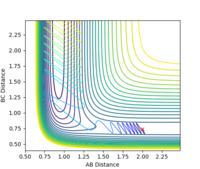 |
yes |
| 2.8 |  |
no | -2.8 | 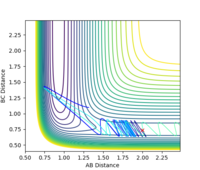 |
no |
| 2.9 | 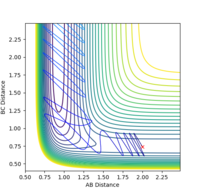 |
yes | -2.9 |  |
no |
| 3.0 |  |
no | -3.0 |  |
no |
According to the results, it can be seen that the reaction is easier to happen when the pHH value is small. Another observation is that when pHH is positive, the reaction is easier to happen. This could be justified by a positive momentum means force in separating the H-H bond, which could help generating the product.
Q: In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
A:
When the condition is set as: A-B distance = 2, B-C distance = 0.74, AB momentum = -0.5, BC momentum = 2.0. The pathway is reactive as shown below.
The internuclear momentum vs. time graph is shown below. Two things can be seen. Firstly the bond vibration of the molecule get more violently after reaction. Secondly, the momentum of H-H becomes positive, which means whey are moving away from each other. This means traslational energy is being transferred to kinetic energy. In experiment, this could be measured by measuring the temperature of the reaction mixture. When translational motion is reduced, the temperature could be expected to decrease.
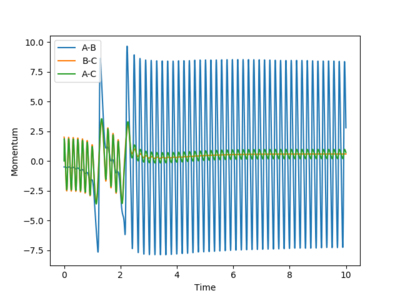
(Careful - not the translational energy is converted, but potential energy is converted to vibrational energy, the latter of which is a type of kinetic energy. Fjs113 (talk) 21:36, 10 May 2018 (BST))
Q: For the same initial position, increase slightly the momentum pFH = -0.8, and considerably reduce the overall energy of the system by reducing the momentum pHH = 0.1. What do you observe now?
A: The profile is shown below. The total energy of the system has been reduced quite a lot, but it is still reactive. This means translational energy is probably more important in crossing the activation barrier.
Q: Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
A: The total energy was set to be fixed. Momentum of AB + BC = 8.5, different situations were tried out.
| pHF value | pHH value | picture | reactive? |
|---|---|---|---|
| 0.0 | -8.5 | File:-8.5.png | yes |
| 0.5 | -8.0 | 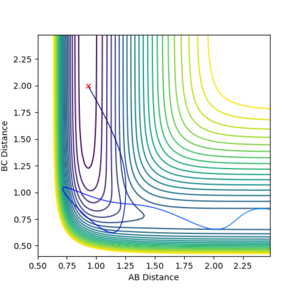 |
yes |
| 1.0 | -7.5 | 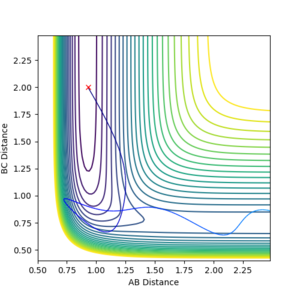 |
yes |
| 1.5 | -7.0 |  |
no |
| 2.0 | -6.5 | 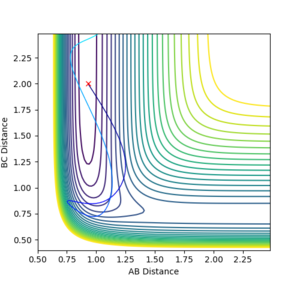 |
no |
It can be seen that when total energy is conserved, the larger the translational contribution, the more likely the reaction to react. Also, according to Polanyi's rule, vibrational energy is more efficient in promoting a late-barrier reaction than translational energy, and the reverse is true for a early transition state reaction. This reaction is a early transition state reaction, so the observation here fits in the rule.