MRD:BR516
BR516 Molecular reaction dynamics
Excercise 1: H + H2 system
What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
The transition state is the maximum energy point on the minimum energy trough as a saddle point. This transition state has a potential energy gradient of 0 with respect to rAB and rBC. This transition point is a maximum in one direction yet a minimum in another.
(All correct, but what is "one direction" and "another"? What you mean is commonly called the reaction coordinate and its orthogonal coordinate. Fjs113 (talk) 18:26, 3 June 2018 (BST))
The minima, however, are minimums in both directions as ∂2V/∂rAB > 0 and ∂2V/∂rBC > 0. This means any variance in the length of rAB or rBC will lead to an increase of energy, indicating that these regions represent the stable reactants and products.
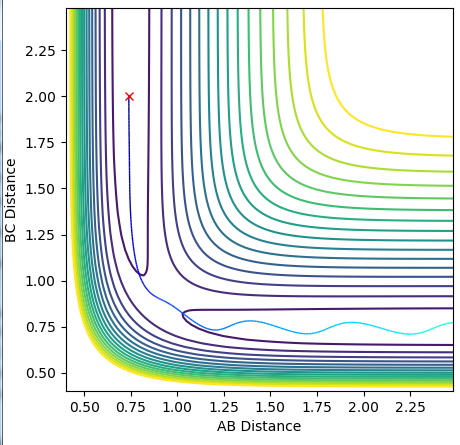
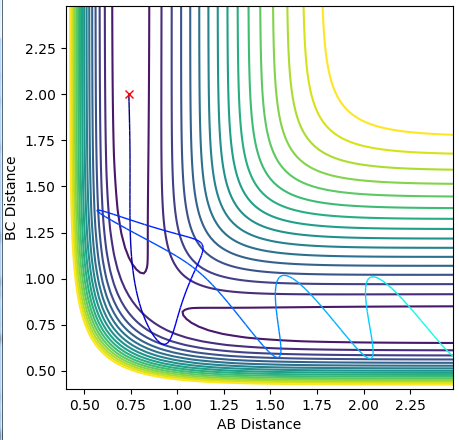
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
Due to the fact that this reaction involves 3 identical atoms, at the transtion state, rAB=rBC. Buy setting the reactants to have no initial momentum, they wont have nay energy to escape the minimum path. By varying the values of rAB and rBC, and observing the “Internuclear Distances vs Time” plot, the transition state distance can be found as this will have no variation in distance with time. rts was found to be 0.908
Comment on how the MEP and the trajectory you just calculated differ.
The MEP (minimum energy path) shows the path of the reaction if the molecules have 0 inertia. This allows the calculation to trace the lowest energy path the reaction could possibly take, the "floor" of the trough in the potential energy surface. The dynamic trajectory takes into account the momentum of the particles. This causes the slight oscillation along the same rough path, as shown by the dynamic plot.
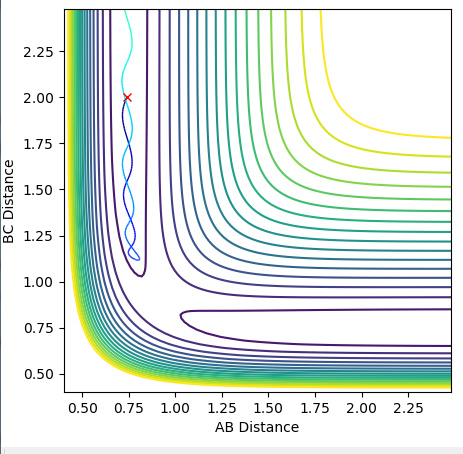
Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.
| p1 | p2 | Total Energy | Reactive/Unreactive | Contour plot | Description |
|---|---|---|---|---|---|
| -1.25 | -2.5 | -99.018 | Reactive |  |
The stationary H-H molecule reacts with another colliding H with the correct momentum, and a new H-H bond forms. |
| -1.5 | -2.0 | -100.456 | Unreactive |  |
An oscillating H-H molecule collides with an H, but not with enough momentum to form a new bond so they are repelled. |
| -1.5 | -2.5 | -98.956 | Reactive |  |
An oscilating H-H molecule collides with another H to form a new bond with a higher vibrational frequency |
| -2.5 | -5.0 | -84.956 | Unreactive |  |
A stationary H-H molecule collides with another H to form a new bond, however the H has too much momentum, and is repelled by the B molecuels nucleus. This causes The AB molecule to remain intact with a much larger vibrational mode, and causes the BC distance to increase as it is repelled. |
| -2.5 | -5.2 | -83.416 | Reactive |  |
The AB molecule of H-H collides with the C molecule of H, but unlike in the above condition, The C molecule has enough momentum to recross the transition state region. The BC bonds forms, Breaks into an AB bond then reforms into the BC bond. |
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
Transition state theory splits the reaction into 2 distinct areas: the reactant and product space. It states that the reactants must cross the energy threshold of the saddle in the transition area to reach the product space. It also assumes atoms obey the laws of classical mechanics using the Born-Oppenheimer approximation, and that each reaction only has 1 saddle point and 1 transition state.
We can see from the above scenarios that for molecules with high momentum, the transition state can be recrossed, so the transition state prediction for reaction rate values will not provide an close approximation to experimental vales run at high temperatures. Therefore, the transition state theory should only be used for reactions at low temperature conditions for predicting reaction rates.
EXERCISE 2: F - H - H system
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
The F + H2 -> FH + H reaction is exothermic, while it's opposite reaction FH + H -> F + H2. This is due to the greater relative strength of the H-F bond (565 kj/mol) to the H-H (432 kj/mol)bond, meaning more energy has to be used to break the H-F bond than is gained forming an H-H bond[1].
(Would've been better if you used the potential energy surface generated by the program to show this. Fjs113 (talk) 18:26, 3 June 2018 (BST))
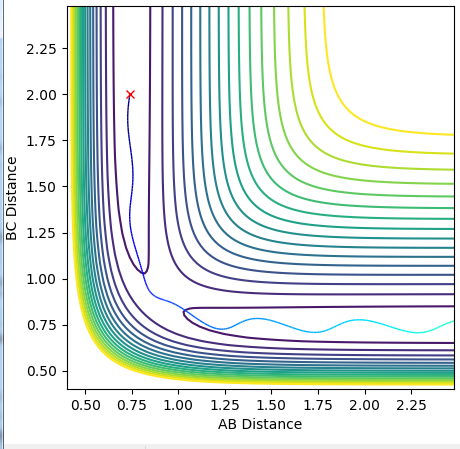
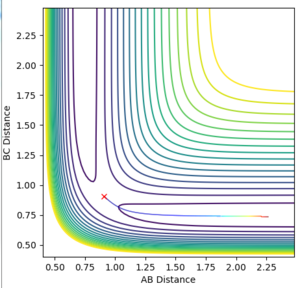
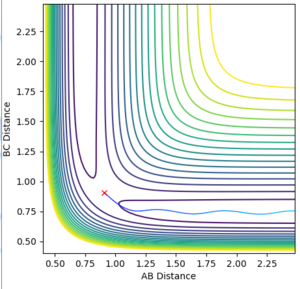
Locate the approximate position of the transition state.
The transition state of the F - H - H system is found at a distance of 0.745 between H-H and 1.811 between H-F. The Momenta of all particles were set to 0 and the initial distance between them varied until an initial distance was found that would remain constant over time.
(Correct, but you did not explain why there is no movement at the TS. Fjs113 (talk) 18:26, 3 June 2018 (BST))
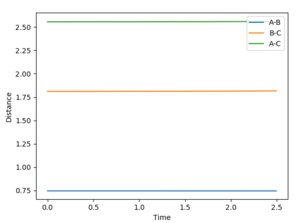
Report the activation energy for both reactions
To find the activation energy, the MEP was found for both the formation of H2 and HF from the H-H-F transition state. The minimum energy point from both products was found, and using this value the activation energy can be found (difference between the maximum energy of the saddle and the minimum energy of the products). H-H-F to HF MEP: Initial energy -103.869, product energy -133.858. Activation energy of HF + H -> H2 + F = +29.989 H-H-F to H2 MEP: Initial energy -103.869, product energy -103.941. Activation energy of H2 + F -> HF + H = + 0.072
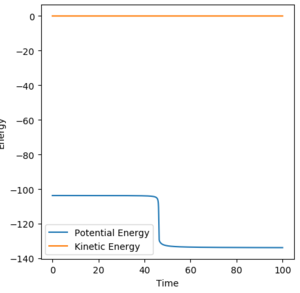
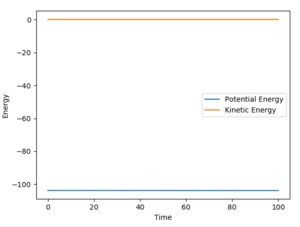
(You can zoom in on this graph to show the slight drop in potential energy! Fjs113 (talk) 18:26, 3 June 2018 (BST))
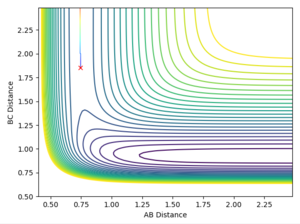
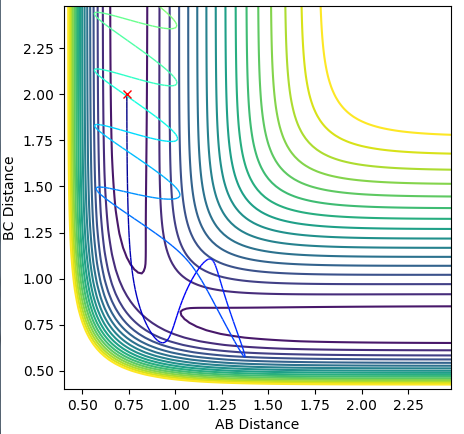
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
Using the reaction condition of A=H, B=H, C=F, rAB = 0.8, rBC = 2.0, pAB = 1, pBC = -1.5, a successful reaction can be seen of the formation of HF. The reaction energy is converted from potential to kinetic, as shown by the vast increase in magnitude of vibration of H-F as compared to the initial H2 molecule. Experimentally, this would be shown by a large increase in temperature of the reaction mixture caused by the increase in average kinetic energy.
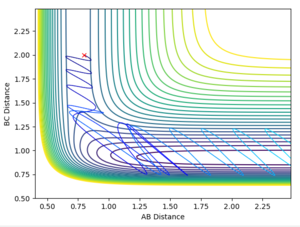
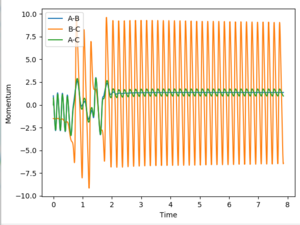
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
Polyani's rules link the effect of vibrational and translational kinetic energy on a reaction. They state that if the reaction has an early transition state close to the energy of the products, translational energy is more important for promoting a successful reaction. Conversely, if a reaction has a late transition state, a higher vibrational energy will promote a more successful reaction.
For the reaction of HF + H -> H2 + F, a higher vibrational energy of the HF molecule is required, as stated by polyani's rules. This is due to the relatively late transition state of the endothermic reaction. Similarly for the reverse reaction, very little vibrational energy is required and only a slight amount of translational energy is required due to the low activation energy of the exothermic reaction.
(You should use some trajectories to show your point here. Fjs113 (talk) 18:26, 3 June 2018 (BST))
References
[1] http://www.wiredchemist.com/chemistry/data/bond_energies_lengths.html, accessed 19/05/2018