MRD:BPW16Y2

Exercise 1 - HHH System

Distinguishing Between a Minimum and Transition State on a Potential Energy Surface

Figure 1 - Potential energy surface showing trajectory across lowest energy pathway.

Figure 2 - Potential energy surface showing maximum character.

Figure 3 - Potential energy surface showing minimum character of reactants.

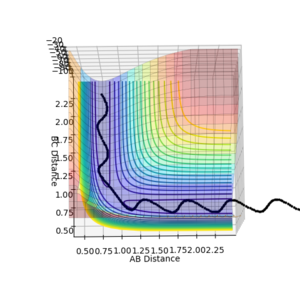
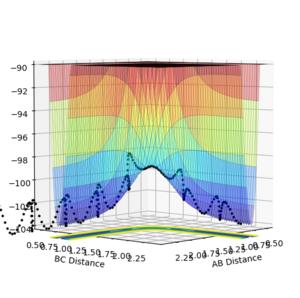
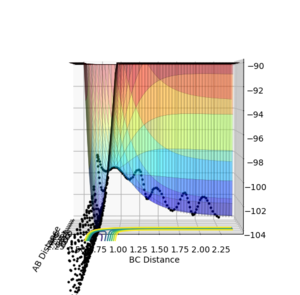
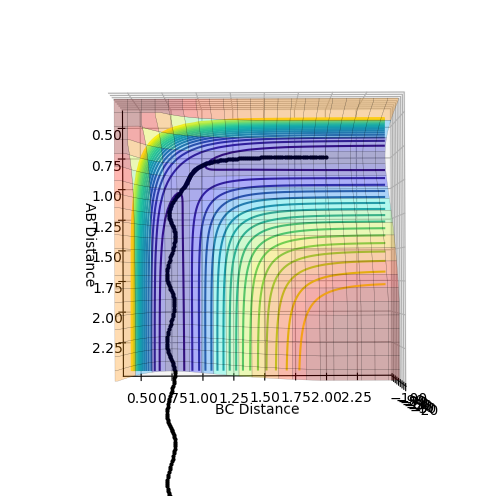
These plots were obtained with the parameters of H1H2 distance = 0.74 Å, momentum = 0, H2H3 distance = 2.30 Å, momentum = -2.7.

At a transition state or a mimimum, the first derivative of the potential energy with respect to each distance (r1 and r2) will be equal to zero. To determine whether the point is a minimum or a transition state, the second derivative of the potential energy with respect to r1 and r2 must be taken (these are orthogonal axes). If the result of this gives two positive values, the point is a minimum (figure 3), while if the result of this gives one negative value and one positive value, the point is a local maximum, hence the transition state (figure 2).

(You need to clarify, that here we are taking the second partial derivative. Also, the transition state is not a local maximum, but rather a saddle point! Fjs113 (talk) 17:41, 28 May 2018 (BST))

Determining the Transition State Trajectory Distance

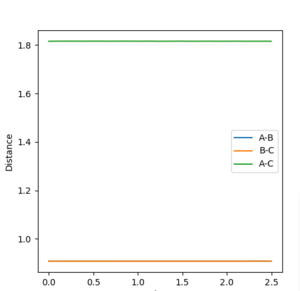
The internuclear distance in the transition state can be determined through a plot of internuclear distance vs time, where we set both momenta to zero. The transition state can then be found my testing different values of the internuclear distances until there is no oscillation observed on the plot. This corresponds to a sphere sitting on the top of the maximum, and having no momentum, so it just 'sits there'. There would be no gradient in the direction orthogonal to the maximum point, hence the trajectory will just oscillate on the maximum point and never 'roll off'. The value determined was 0.9076 Å, to 4 d.p, as can be seen from figure 4.

Figure 4 - Internuclear distance vs time plot for the H + H2 trajectory with equal bond lengths.

Comparing MEP and Dynamics Calculation Methods

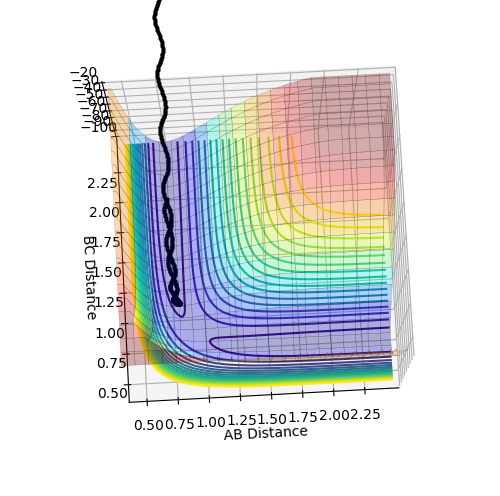
Figures 5 and 6 show the PES for when r1 = 0.9176 Å and r2 = 0.9076 Å (i.e. slightly displaced from each other).

Figure 5 - Potential energy surface calculated with MEP.

Figure 6 - Potential energy surface calculated with Dynamics.

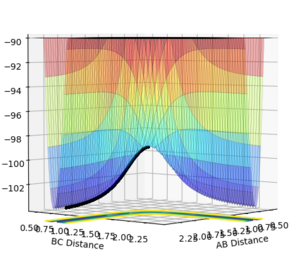
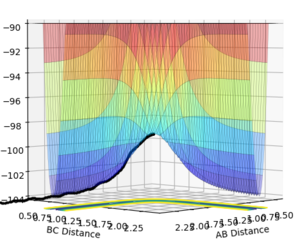
MEP is the minimum energy pathway for the trajectory. It corresponds to infinitely slow motion of the species. However, the MEP does not give a realistic account of the motion of the atoms during the reaction since the atoms have a mass, and hence their motion will be inertial.

The MEP plot shows the pathway for the species coming together if we treat them as two solid entities. The dynamic plot treats the system as a diatomic molecule and a single atom. Hence, as can be seen from the figures 5 and 6, the MEP plot does not show any oscillation, as there is no vibrational energy, but the dynamic plot shows oscillations and hence vibration energy of the diatomic.

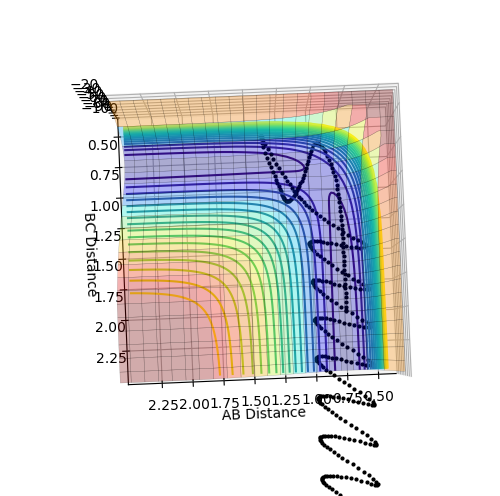
Testing Different Reaction Trajectories to Determine Reactivity

Table 1 - Testing different reaction trajectories

p1	p2	Reactivity	Total Energy (kcal/mol)	PES	Comments
-1.25	-2.5	Reactive	-99.119		This trajectory is a productive reaction, with reactants passing through the transition state and becoming products, ie AB + C --> A + BC. For this to occur, the reactants must have had enough energy to overcome and traverse the transition state energy maximum. It can be seen that the reactant, AB, has no vibrational energy, as the trajectory does not oscillate in that region, however it does for the product, showing that BC had vibrational energy. This energy would have been converted from translational (kinetic) energy when the two reactant species collided.
-1.5	-2.0	Unreactive	-100.456		This trajectory is non-productive, with the reactants reaching the transition state but rather than forming products they go back on themselves. This corresponds to the reactants, AB and C, not having enough energy to overcome the transition state energy barrier and hence do not form products. The diatomic simply 'bounces off' the third atom, moving in the reverse direction to what it started of as. It can be seen that the diatomic AB has vibrational energy before the collision and after. AB will have gained some more vibrational energy from the collision as translational energy will have been converted into vibrational energy, in order to obey the conservation of energy. It has been calculated that this energy has a lower total energy than system one, and therefore does not have enough energy to overcome the transition state energy barrier.
-1.5	-2.5	Reactive	-98.956		This shows a productive reaction where AB + C turns into products A and BC after passing successfully through the transition state region. It has been calculated that this system has a higher energy that the first two systems studied, and hence can overcome the transition state energy barrier and cross it to form products. It can also be seen that both the reactant and product diatomics, AB and BC respectively, have vibrational energy and so the trajectory oscillates.
-2.5	-5.0	Unreactive	-84.956		The trajectory here is unproductive, with reactants not forming products at the end of the reaction. The reactants, AB and C are able, momentarily, to form products (A and BC). Therefore, the reactants must have contained enough energy to cross the transition state maximum. However, most likely due to the large vibrational energy gained from the transfer of translational energy into vibrational energy when the species collide, there is so much vibrational energy in the diatomic BC that the bond dissociates. This now produces three single atoms, A, B, and C. Atom A is moving in direction of atom B and hence they react to form the reactant species, AB, again, but now possessing a great deal of vibrational energy (but not so much that the AB bond breaks). The energy of the system is higher than any of the ones studied previously, showing that there is enough energy to break the BC bond when it forms.
-2.5	-5.2	Reactive	-83.416		This plot is a productive reaction. It can be seen that the reactants, possessing no vibrational energy in the diatomic, are able to reach and cross the transition state energy barrier to form products. However, the product diatomic, BC, then dissociates to reform the reactants, as it must have a high amount of vibrational energy, which has been converted into it from the high amount of translational energy in the reactants. When the BC molecule dissociates it sends atom B in the same direction as atom A, so these two can react together to reform the reactant diatomic, AB. It can be seen from the plot that when this occurs, AB is formed in a vibrationally excited state, having enough energy to break apart again and react successfully with atom C this time, to form products of BC and A. The BC product diatomic has a large amount of vibrational energy. This is an example of barrier recrossing.

Transition State Theory

In Transition State Theory, a reaction is described by considering the motion of atoms. The Born-Oppenheimer approximation is applied and the motion of the nuclei and electrons are separated, given that nuclei are much heavier than electrons. Following this, the motion of the atoms can be treated classically using Newton's laws of motion. This neglects the fact that vibrations are quantised or that tunneling can happen through quantum mechanics. Another assumption is that the transition states obey a Maxwell-Boltzmann distribution shape and that the species have to collide with enough energy for a reaction to be successful, i.e. to pass over the transition state barrier, however this is not always the case in reality due to quantum tunneling effects.

Transition state theory says that activated complexes exist in a type of equilibrium, quasi-equilibrium, with the reactants, and that these complexes can convert into products. By using rate equations such as the Arrhenius or Eyring equations, the rate of reaction can be found. The transition state will be a saddle point on the PES. The quasi-equilibrium point means that reactants are in equilibrium with the activated complex, but the activated complex is not in equilibrium with the products, i.e. once the transition state has been traversed, the products can not reform the reactants. Another downfall of transition state theory is that, especially at higher temperatures, the trajectory does not always pass through the lowest energy saddle point in the PES, as higher energy vibrational modes are populated.

For systems 1 to 3 studied above, the predicted reaction rates through transition state theory are likely to match well with experimental values, as either the reactants simply cross the transition state barrier to form products, or do not have enough energy to react at all. For systems 4 and 5 however, the rates are likely to differ from predicted values as these systems show barrier-recrossing, where once products have formed, they actually cross back over the transition state barrier and reform the reactants, something that is not 'allowed' in transition state theory. The higher temperature idea could be seen through systems 4 and 5 having higher momenta than in 1 to 3.

(Very good. Fjs113 (talk) 17:41, 28 May 2018 (BST))

Exercise 2 - FHH system

Classifying the Reaction Thermodynamics

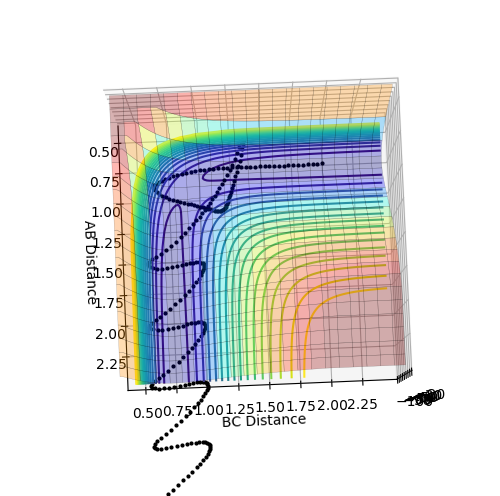
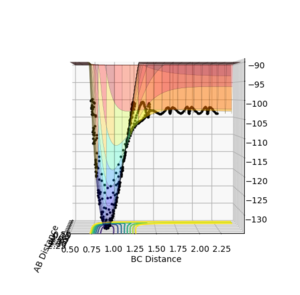
From figures 7 and 8 it can be seen that the reaction of H2 + F is exothermic as the products, HF + F (with the diatomic distance of HF labelled as BC on the plot) is lower in energy than the reactant species, H2 and F. It is therefore the case that the reverse reaction, HF + H is an endothermic. This can be related to the relative bond strengths: clearly the HF bond is much stronger than an H-H bond. This is due to the difference in electronegativity in HF, creating an ionic contribution to the bond, making it stronger, hence energy is released when HF forms from H2 and F.

The parameters used were H1H2 (diatomic) distance = 0.74 Å, momentum = 0, H2F distance = 2.30 Å, momentum = -2.7.

Figure 7 - PES showing overall exothermic reaction of H2 + F.

Figure 8 - PES showing how the products HF + F are lower in energy than HH + F.

Determining the Transition State

To determine the transition state, I first looked at the internuclear distance vs time plot (figure 9) from the trajectory plotted in figures 7 and 8. The transition state will be in the region where the AB and BC lines cross over, i.e. between 0.7 and 0.8 seconds approximately. To determine the transition state accurately, The momenta for each species, H2 and F, were set to be zero, and the distances AB and BC varied until there was no oscillation observed in either line, corresponding to the H-H-F activated complex at the very top of the peak of the transition state, and not 'rolling' to either reactants or products. This can be seen in figure 10, where the HH (AB) distance is 0.745 Å and the HF (BC) distance is 1.811 Å.

Figure 9 - Internuclear distance vs time for reactive trajectory

Figure 10 - Internuclear distance vs time for transition state

Determining the Activation Energy

Figure 11 - Energy vs time plot showing the energy change for HF + H.

Figure 12 - Energy vs time plot showing the energy change for HH + F.

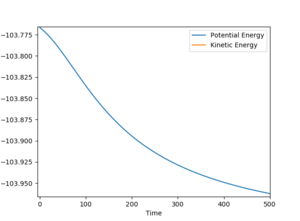
To find the activation energy, I used an MEP calculation and displaced one of the distances slightly from the transition state distances determined previously. This meant that, depending on which distance was changed, the trajectory would fall from the transition state maximum and simply roll to the valley floor of either the reactants or products. The activation energy was then calculated from the difference in potential energy on an energy vs time graph.

HF + H --> H2 + F Activation energy = 29.969 kcal/mol

H2 + F --> HF + H Activation energy = 0.200 kcal/mol

Reaction Dynamics

A productive, reactive trajectory, where H2 + F turn into HF + F products was found with the initial conditions of HH(0.79 Å, momentum = 0.78), HF(1.8 Å, momentum = -0.5).

Figure 13 - Contour plot showing productive trajecotry.

Figure 14 - Surface plot showing productive trajectory.

Figure 15 - Internuclear momenta vs time graph for reactive conditions.

Figure 16 - Energy vs time graph for reactive conditions.

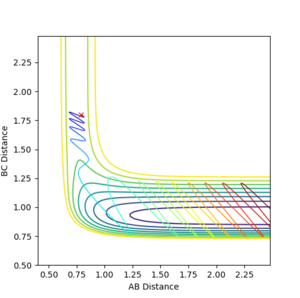
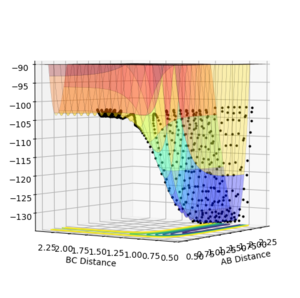
It can be seen from the contour plot, that the product diatomic, HF, is formed in a vibrationally excited state, and continues to oscillate, possessing vibrational energy. From the energy vs time, graph it can be seen that the conservation of energy principle is obeyed, as when the potential energy is at a maximum in an oscillation, the kinetic energy is at a minimum, and vice versa. The vibrationally excited HF molecule will release its energy to the surrounds as heat most likely, colliding with other gas molecules. A way to experimentally test this prediction would be to obtain a gas-phase FTIR spectrum of the HF produced, and this should show relaxation from the vibrational excited state to the ground state. A photon would be emitted corresponding to the difference in energy between the first excited and ground electronic states.

Polanyi's Empirical Rules

Polanyi's empirical rules state that vibrational energy is much more efficient at activating a late transition state reaction than translational energy. The opposite is true for an early transition state, where translational energy is more effective than vibrational energy. In order to test these rules, different initial momenta were set up. The H2 + F --> HF + F reaction is exothermic, as seen in figure 7, and hence through the Hammond postulate will have an early transition state, with the transition state structure resembling the reactants. Therefore, the reaction should be initiated more effectively with translational energy, rather than vibrational energy. The opposite is true for the HF + H --> H2 + F reaction, which is endothermic and hence will have a late transition state, and being initiated more effectively with vibrational energy.The quick brown fox jumps over the lazy dog. (Not sure if meant to be here or not? ;) Fjs113 (talk) 17:41, 28 May 2018 (BST))

Table 2 - Testing different Reaction Momenta For H2 + F

p(HH) (Vibrational Energy)	p(HF) (Translational Energy)	Plot
-2.8	-0.5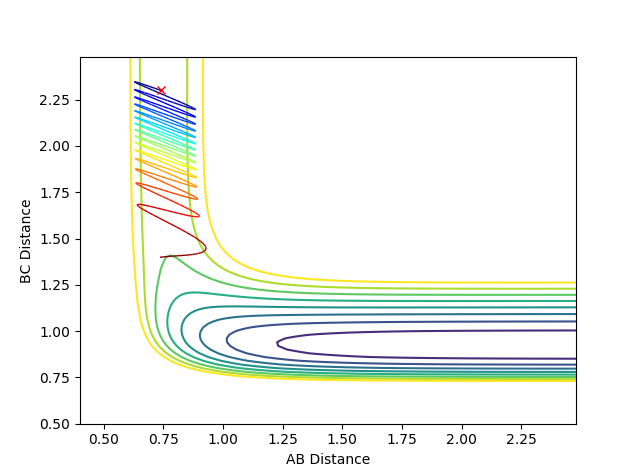
-0.5	-2.0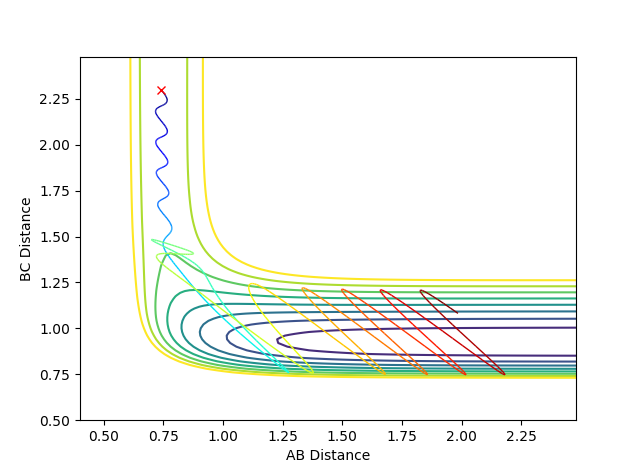

Table 3 - Testing different Reaction Momenta For HF + H

p(HF) (Vibrational Energy)	p(HH) (Translational Energy)	Plot
-0.4	-6.7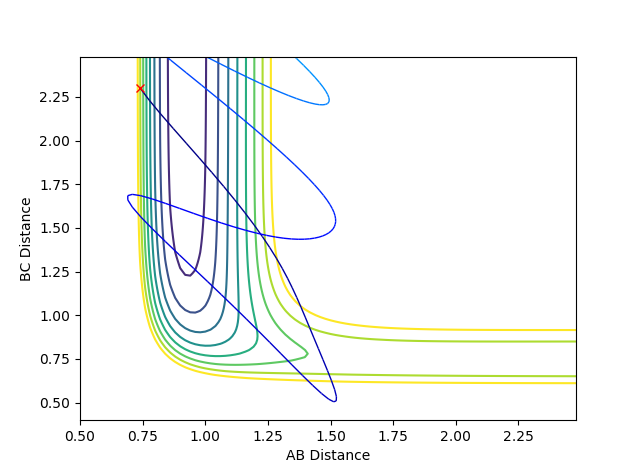
-6.7	-0.4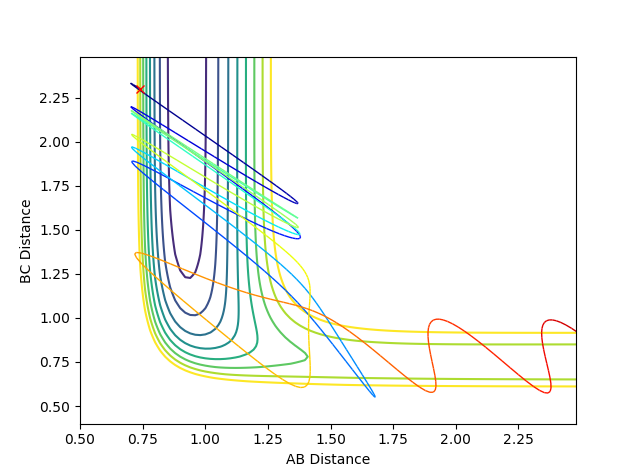

It can be seen from table 2 that a greater weighting of translational energy rather than vibrational energy drives the exothermic, H2 + F --> HF + F, reaction, with an early transition state, forming the products after successfully passing over the transition state barrier. However, a greater weighting of vibrational energy does not lead to a productive reaction. It can be seen from table 3 that the opposite is true, with an excess of vibrational energy driving the endothermic reaction, with a late transition state, forming products of H2 and F, whereas an excess of translational energy does not give a reactive, productive trajectory. These results are in agreement with Polanyi's empirical rules.