MRD:AMM416 Molecular Dynamics Y2
H + H2 System
Dynamics from the transition state region
1. What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
At both transition state (TS) and minimum structures, which are saddle points or stationary points, the gradient of the surface potential is equal to zero. To distinguish them, the second derivative of the gradient has to be calculated. If its value is greater than 0, the structure is at a minimum energy. However, if the value is less than zero, the structure is at a maximum energy, hence at the transition state.
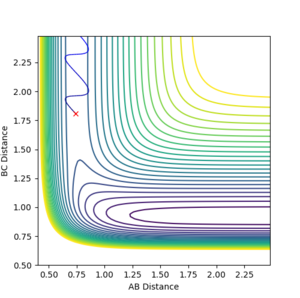
2. Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
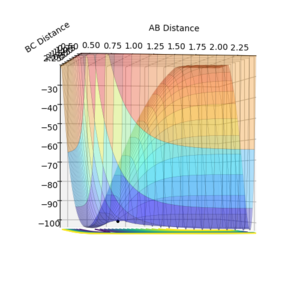
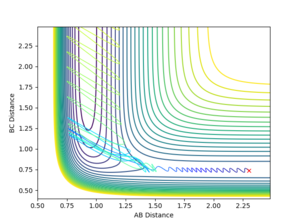
From the initial conditions used in the exercise before, the TS was found approximately at r=0.75. Hence, values greater than that were tried while displaying the surface potential for each. At r=0.91, the black trajectory in the surface potential was just a dot resting on the ridge (Figure 1), suggesting that at this point the structure was stable at the TS. As seen in the inter-nuclear distance vs. time graph below (Figure 2), there is no formation of the A-B graph, which is the product of the collision, hence suggesting that the reactants are oscillating at the transition state.
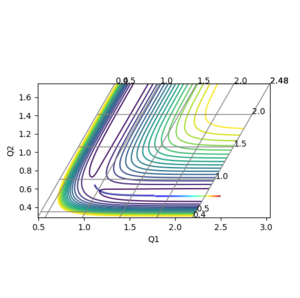
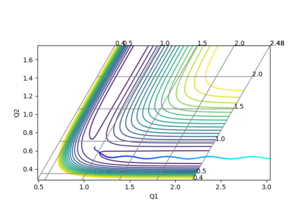
3. Comment on how the mep and the trajectory you just calculated differ.
In MEP, the trajectory does not show any vibrational motion, while the trajectory calculated with Dynamics shows oscillations as seen in Figure 3 and 4.
Ng611 (talk) 20:00, 24 May 2018 (BST) True, but why is this the case? How do the procedures differ?
Reactive and unreactive trajectories
4. Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.
| Entry | p1 | p2 | Total Energy/kcalmol-1 | Contour Plot | Reactivity | |
|---|---|---|---|---|---|---|
| 1 | -1.25 | -2.5 | -99.018 |  |
Reactive: trajectory goes through transition state and exits through product channel. | |
| 2 | -1.5 | -2.0 | -100.456 |  |
Unreactive: trajectory reaches transition state but turns around to exit reactants channel. | |
| 3 | -1.5 | -2.5 | -98.956 |  |
Reactive: trajectory goes through transition state and exits through product channel. | |
| 4 | -2.5 | -5.0 | -84.956 |  |
Unreactive: trajectory reaches transition state and recrosses the barrier. However, it turns around to exit reactants channel. | |
| 5 | -2.5 | -5.2 | - 83.416 |  |
Reactive: trajectory reaches transition state and recrosses the barrier. It manages to go through the transition state and to exit the products channel. |
5. State what are the main assumptions of Transition State Theory (TST). Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
TST is based on three main assumptions:
1. The activated complex is in equilibrium with the reactants.
2. The reactant nuclei behave like classical masses.
3. The reaction pathway proceeds by lowest energy transition state on the PES.
Nevertheless, from the results obtained in Table 1, the assumptions made in TST fail to represent the actual reality. First of all, if the nuclei behaved classically, all the collisions with enough total energy will be reactive. Therefore, Reaction 5 should be reactive but barrier recrossing occurs, which makes the reaction actually unreactive. Barrier recrossing is not predicted by TST, and neither are the other reaction pathways such as quantum tunneling. Hence, the rates of reaction calculated using TST will be larger than the experimental ones due to the negligence of the other pathways.
Ng611 (talk) 20:02, 24 May 2018 (BST) Good! Tunelling is an important effect, but TS recrossing has a far greater influence on the reaction. Remember to state that TS theory assumes that once the TS is crossed, then no recrossing takes place as it is the most important assumption in this context.
F-H-H System
PES Inspection
1. Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
The F + H2 reaction is exothermic. The product is HF and the H-F bond is relatively strong due to the large difference in electronegativity of H and F, therefore the energy of the products is more negative than the energy of the reactants and energy is released at the end of the reaction. On the other hand, the H + HF reaction is endothermic due to the weaker H-H bond formed as the product. Therefore, the energy of the products is more positive than the energy of the reactants and energy is absorbed by the system from the surroundings at the end of the reaction.
2. Locate the approximate position of the transition state.
From Hammond's postulate, if the reaction is exothermic, the structure and energy of the transition state will resemble the reactants. While for endothermic reactions, the transition state will resemble the products.
F + H2:
Since the reaction is exothermic, the transition state will resemble the reactants. So the H-H bond won't be too different from the standard H-H bond in H2. The H-H bond length is 0.740 Å, therefore by optimising the initial conditions, it was found that the structure oscillates at the transition state when the H-F distance is 1.81 Å.
H + HF:
The reaction is endothermic so the transition state will resemble the products. Thus, the distance between the H atoms in the transition state will be similar to the H-H bond length in H2 and the transition state is found when the H-F bond length is 1.81 Å, as in the F + H2 reaction, since H + HF is the reverse reaction of F + H2.
3. Report the activation energy for both reactions.
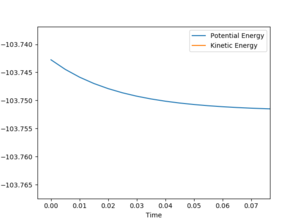
The activation energy (Ea) is equivalent to the energy difference between the maximum of the transition state and the minimum of the reactants. The energy of the transition state is calculated by the program, while the energy of the reactants is simply the sum of the bond enthalpies of the species involved, which are also retrieved from the program by separating the reactants by a large distance and keeping the bond lengths of H-H (in F + H2) and H-F (in H + HF) as the standard bond lengths. For both reactions, the energy of the transition state was found to be -103.743 kcalmol-1 (Figure 5):
Ea(F + H2) = -103.743 - (-104.020) = 0.277 kcalmol-1
Ea(H + HF) = -103.743 - (-133.954) = 30.211 kcalmol-1
Reaction Dynamics and Polanyi's Empirical Rules
4. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
For the F + H2 reaction, a reactive trajectory was found by setting the initial conditions as following:
rF-H = 2.3
rH-H = 0.74
pF-H = -1
pH-H = -5
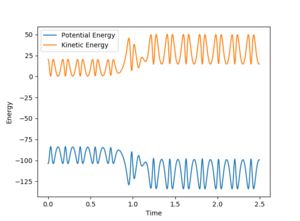
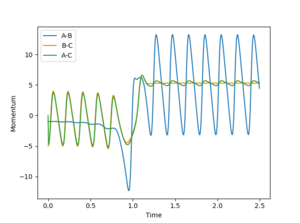
Energy is conserved at the end of the reaction as seen from Figure 6; kinetic and potential energies are exchanged throughout the reaction. As seen from the Internuclear momenta vs. Time graph (Figure 7), the H-H bond in the reactants oscillates with less maximum displacement than the H-F bond in the products. Therefore, it suggests that the energy released in the exothermic reaction is used to make H-F vibrate with a greater amplitude. To confirm it experimentally, IR spectroscopy can be employed to measure the vibrational energy of the reactants compared to the products.
5. Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
Polanyi's empirical rules state that higher amounts of vibrational energy, compared to translational energy, promote reactions with a late transition state, i.e. endothermic reactions. On the other hand, translational energy promotes reactions with an early transition state, i.e. exothermic reactions.
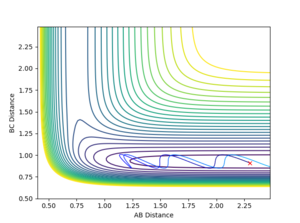
For instance, in the exothermic reaction F + H2, the pF-H represents the translational energy of the F atom and pH-H the vibrational energy in the H-H bond. If pF-H is kept constant at a low value of -0.5 and pH-H is varied using relatively high values between such as -3 and 3, very few reactive trajectories were found (Figure 8), apart from values close to the extreme values chosen: e.g. reactive trajectories at pH-H = -2.8 due to barrier recrossing. However, if the translational energy is slightly increased to -0.8 and the vibrational energy decreased to -0.1, the resulting trajectory is reactive since more translational energy promotes exothermic reactions (Figure 9).
Comparatively, in the endothermic reverse reaction H + HF, the pH-H represents the translational energy of the incoming H atom and pH-F the vibrational energy in the H-F bond. If the translational energy of the H colliding is very large compared to the vibrational energy of HF, the resulting trajectory is unreactive as the H atom bounces of HF (Figure 10). Since this is an endothermic reaction, if the translational energy is decreased and the vibrational energy of the H-F bond is increased, the reaction is successful as vibrational energy promotes endothermic reactions (Figure 11).
Ng611 (talk) 20:05, 24 May 2018 (BST) An excellent second section, and overall a very good report. Well done!