MRD:2Yphyscomplabkk4717

Excercise 1

Ng611 (talk) 12:24, 22 May 2019 (BST) A fairly good report overall. You made a few minor factual slips (e.g.: discussion of the breakdown of TS theory, and experimental determination of energy distribution). One or two of your report also seemed incomplete (missing text, trajectories, etc.).

Question 1

Figure 1. Transition State at the saddle point (Red triangle) and the new x and y axes.

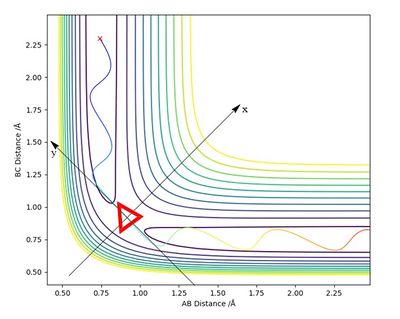
1. On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?

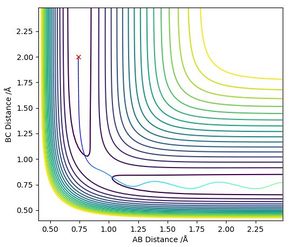
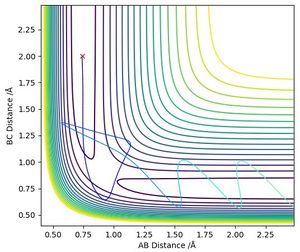
Mathematically, the transition state (TS) is defined as a saddle point on the potential energy surface diagram (Red triangle on Figure 1). A saddle point is where x and y axes by f_x = f_y = 0 and (f_xxf_yy - f_xy²) < 0.

The new y axis is defined as the tangent of the minimum energy pathway at the maximum potential energy. The new x axis is set to be orthogonal to the defined y axis. The new x and y axes are shown on the figure.

The local minima, maxima and the saddle point are all stationary points meaning the first derivation equals 0. However, the local minima and maxima have (f_xxf_yy - f_xy²) > 0, but the transition state is the only point where (f_xxf_yy - f_xy²) < 0.

Ng611 (talk) 12:13, 22 May 2019 (BST) Good answers. Keep in mind that (f_xxf_yy - f_xy²) < 0 finds the TS without the change in co-ordinates you applied. It will still work with your new co-ordinate system (so you are still correct to use it) but it is overkill.

Question 2

2. Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

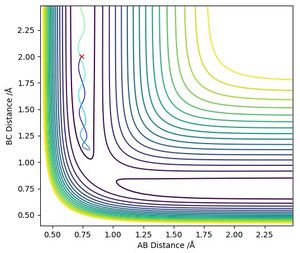
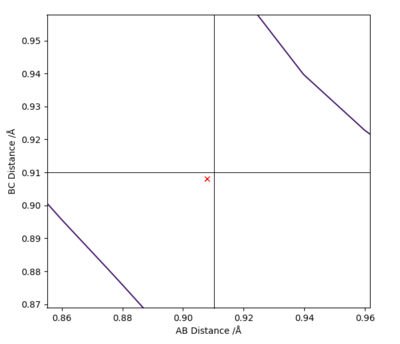
By observation, this reaction is symmetric and therefore the distances between atoms A - B and B - C should be equal at the transition state.

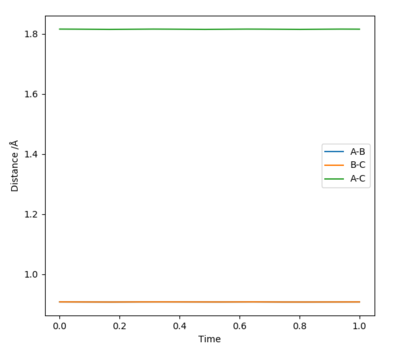
Through trial and error, it was found that the transition state position was at r₁ = r₂ = 0.908 Å (Figure 2). This number was confirmed by an "Internuclear Distances vs Time" plot where no oscillation in distances is seen (Figure 3).

Figure 2. Contour plot to find rts.

Figure 3. Internuclear distance vs Time plot to confirm rts.

Question 3

3. Comment on how the mep and the trajectory you just calculated differ.

Ng611 (talk) 12:15, 22 May 2019 (BST) Where are your trajectories?

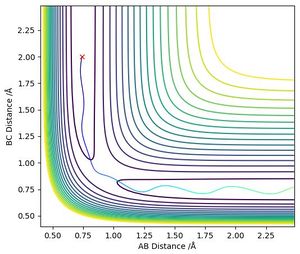
The calculated Minimal Energy Pathway shows the trajectory from a non negative gradient to the local minima. If the starting point is exactly at the transition state then the MEP remains just a point on the graph. When the radius between two of the atoms was changed by 0.1 then the MEP traced the gradient to the minima and stopped.

The same situation with a dynamic calculation did not stop at the minima but continued moving out of the graph due to the hydrogen atom and the molecule continuing separating from each other due to conservation of momentum. Another difference is that the dynamic calculation also showed vibrations between the atoms in the H₂ molecule.

Question 4

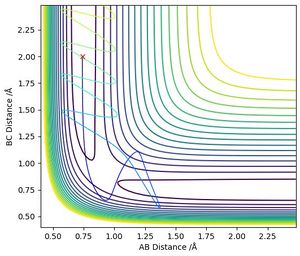
4. Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?

	p1	p2	Etot	Reactive?	Description of the dynamics	Graph
a)	-1.25	-2.5	-99	Yes	Non-vibrating molecule A-B slowly collides with atom C and react. Atom A and very slowly vibrating molecule B-C separate.	Figure 5a. Plot of trajectory a.
b)	-1.5	-2.0	-100	No	Vibrating molecule A-B collides with atom C without reacting and then separate from each other.	Figure 5b. Plot of trajectory b.
c)	-1.5	-2.5	-99	Yes	A non-vibrating molecule A-B collides with an atom C reacting. The new atom A and a slightly vibrating molecule B-C separate.	Figure 5c. Plot of trajectory c.
d)	-2.5	-5.0	-85	No	Non-vibrating molecule A-B collides with atom C and after momentarily dissociating, A-B molecule reconnects and separates vibrating.	Figure 5d. Plot of trajectory d.
e)	-2.5	-5.2	-83	Yes	Non-vibrating molecule A-B bounces off of atom C causing A-B to dissociate. Atom A and vibrating molecule B-C then separate.	Figure 5e. Plot of trajectory e.

The calculations in the table contradict the theory that all reactions occur when the particles start at the same coordination and have a total energy higher then the activation energy. With increasing momenta, some collisions result in momentary dissociation but end up reforming the initial molecule.

It is therefore seen that the occurring of a reaction depends highly on the relative positions and not only the momenta at the collision even when the energy is higher than necessary to overcome the activation barrier.

Activation energy:

Ng611 (talk) 12:17, 22 May 2019 (BST) Not sure what this answer means. I'm assuming you meant to complete this?

Question 5

5. State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

Although the Transition State Theory (TST) is useful in many situations, it is based on some assumptions that result in the theory breaking down in more complex situations. There are three main assumptions in the theory:

1. The first assumption is that the particles follow classical physics and any reaction able to overcome the activation barrier happens. In reality, reactions that do not have the necessary energy might also occur according to quantum mechanics. This is more relevant for low activation energy reactions where quantum tunneling is more probable. The classical physics also fail to predict situations where there is enough energy to overcome the activation barrier but due to electrostatic interactions, the reaction still does not take place.
2. Secondly, TST assumes that in a multi-step reaction, all intermediates reach a Boltzmann distribution before further reactions take place. However this is not always the case. If the intermediate is short-lived, the reaction trajectory can bypass the intermediate equilibrium and result in different reaction kinetics to those predicted by TST.
3. Finally, the theory is insufficient at high temperatures where the energy at collision is higher than the activation barrier. In this case the transition state at the saddle point might not be crossed due to stronger vibrations or other non-translational interactions between the reacting particles.

The calculations made above also show how the Transition State Theory does not always predict the reaction correctly. All collisions in the table in question 4 exceed the activation energy and according to the TST should therefore result in reactions. However, in situations (b) and (d) the reaction does not occur which shows the limitations of the theory.

Ng611 (talk) 12:18, 22 May 2019 (BST) You're partially correct. The total momenta does change from entry to entry. Really the thing that TS theory fails to predict is barrier recrossing (your final two trajectories)

Excercise 2

PES inspection

By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

Figure 4. Surface plot of a H-H-F with Transition State as a black dot.

The potential energy of H-F is lower than that of H₂ and therefore the reaction between the hydrogen molecule and a fluorine atom is exothermic; and the opposite reaction between the H-F and H atom is endothermic. By Hammond's postulate the transition state resembles more of the reactants in an exothermic F + H₂ reaction and the TS should then be found at a position where the distance between the hydrogen atoms is lower than the distance between colliding hydrogen and fluorine atoms.

The lower potential energy of HF molecule also shows that the bond strength of H-F is stronger than that of H-H.

Locate the approximate position of the transition state.

The Transition State for H_A-H_B-F_C is at distances r_AB = 0.745 Å and r_BC = 1.8107 Å. This was found to be the saddle point.

Report the activation energy for both reactions.

The energies at the stationary points were found to be:

E_TS = -103.75189 kcal/mol;

E_H2 = -104.01974 kcal/mol;

E_HF = -134.02398 kcal/mol.

From the total energies the activation energies were calculated as:

Ea_{F + H2} = 0.268 kcal/mol;

Ea_{H + HF} = 30.272 kcal/mol.

Ng611 (talk) 12:20, 22 May 2019 (BST) Correct EAs, well done

Reaction dynamics

In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.

Figure 5a. Energy conservation plot over time of F + H₂.

Figure 5b. Contour plot of the Energy conservation graph F + H₂.

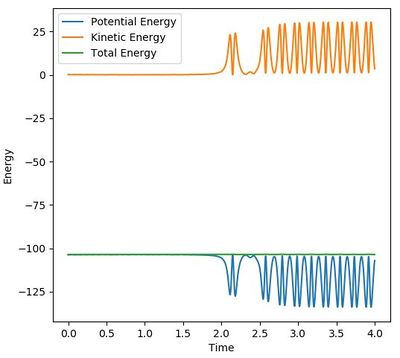
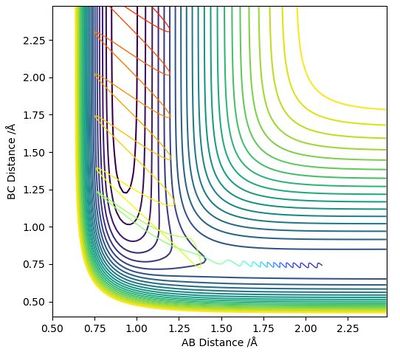
In isolated reactions like F + H₂ , the total energy must be conserved. In this case the potential energy is "released", meaning it is lowered due to the creation of a stronger bond. The released energy from this bond creation is converted to kinetic energy which can be in the form of translation or vibration. With vibration, the energy is periodically converted between kinetic and potential energy (Figure 5ab). Nevertheless, the time-average kinetic energy increased and this is directly related to the temperature of the system.

Experimentally potential energy change to kinetic energy can be observed as the change in temperature in the reaction mixture. For exothermic reactions, an increase, and for endothermic a decrease in total kinetic energy and therefore temperature will occur and to observe that a thermally isolated system with a thermometer is necessary. This type of characterisation is called calorimetry and it is widely used to observe the reaction kinetics and thermodynamics of a system.

Ng611 (talk) 12:21, 22 May 2019 (BST) This will not give you any indication of the distribution of the kinetic energy (whether it's vibrational vs translational)

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Initial kinetic energy in the system can be in the form of translational or vibrational energy and this in turn has an effect on the reactivity of the system. According to Polanyi's rules, increasing translational energy promotes exothermic reactions that have an early transition state. The opposite is true for late transition state, endothermic reactions that occur more often when the kinetic energy is in the form of vibrational energy. In both cases, the total kinetic energy must be higher than the activation energy of the reaction.

Through LEPS GUI simulations, it was confirmed that the reaction is more likely to happen in the endothermic direction with high vibrational and lower translational energy contribution to kinetic energy. However, high vibrational and low translational energy didn't guarantee a reaction as relatively often the reactants reformed after momentarily passing the transition state.

As with Transition State Theory, Polanyi's rules are a helpful as a tool but fail to describe the whole picture. Already in a model where the collision happens one-dimensionally, there are too many factors that affect the reactivity. A collision that leads to a reaction at some conditions might change to unreactive by changing only the initial distance of the colliding particles. It can be therefore concluded that the Polany's rules apply as a general trend but can't be applied for predicting reactivity for specific reaction conditions. Graphs (Figure 6) show working examples of Polanyi's rules where a change in translational and vibrational momentum have a significant influence on the exo- and endothermic reactions respectively.

• 
  Figure 6a. An unreactive exothermic F + H₂ reaction with translational momentum as p_FH = -0.51 and vibrational momentum as p_HH = -0.5.
• 
  Figure 6b. A reactive exothermic F + H₂ reaction with translational momentum as p_FH = -0.52 and vibrational momentum as p_HH = -0.5.
• 
  Figure 6c. An unreactive endothermic H + HF reaction with vibrational momentum as p_FH = -2.5 and translational momentum as p_HH = -0.5.
• 
  Figure 6d. A reactive endothermic H + HF reaction with vibrational momentum as p_FH = -2.6 and translational momentum as p_HH = -0.5.

Ng611 (talk) 12:23, 22 May 2019 (BST) Good examples. You're correct that Polanyi's rules only provide a general trend (they're guidelines, not rules).