MRD:29hb3017

H + H₂ System

Transition States

The transition state is mathematically defined is the point on a potential surface at which ∂V(r_i)/∂r_i=0, where r_i are the interatomic distances in the system. For a three atom system, there are two interatomic distances, r_AB and r_BC. At the transition state, the second derivative of potential energy with respect to one interatomic distance will be less than zero, indicating it is a maxima, and the second derivative of the potential energy with respect to the other interatomic distance will be greater than zero, indicating that it is a minimum point. This can be expressed in symbols as follows: ∂V²(r_AB)/∂²r_AB > 0 and ∂V²(r_BC)/∂²r_BC < 0. The transition state is a saddle point on a potential energy surface, meaning it is both a maxima and minima point and there is no gradient. The transition state can be distinguished from a local minimum of a potential energy surface by looking at the second derivatives with respect to the interatomic separations. For a local minimum, the second derivative of the potential energy with respect to the interatomic separation, r_i will be greater than zero for all r_i but at the transition state one second derivative will be negative and the other will be positive.

good Pu12 (talk) 22:12, 16 May 2019 (BST)

Finding the transition state

Figure 1: A plot of interatomic distance against time when the molecule is in its transition state.

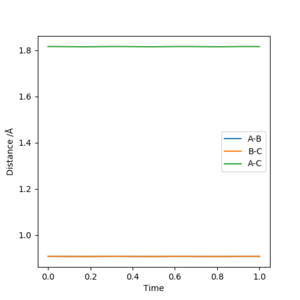
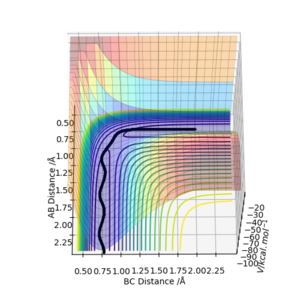
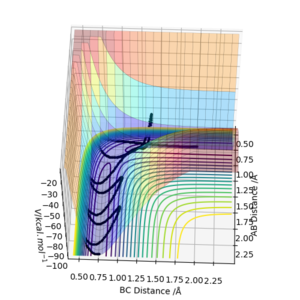
The transition state for the reaction between a hydrogen atom and a hydrogen molecule occurs when the interatomic distances r_AB=r_BC due to the symmetry of the collision. By setting the momenta for p_AB and p_BC to 0 and inputting different values for r_AB and r_BC, the transition state atom separation, r_ts can be found. This distance was found to be 0.9081A. At this separation the interatomic distances are constant(figure 1), showing that the atoms are not oscillating. This shows that there must be no gradient at this point, otherwise the reaction pathway would show the system 'rolling' to a position of lower potential energy. The loss of potential energy would result in the gain of kinetic energy, making the molecule oscillate. Since the molecule is not oscillating, the system must be in the transition state.

The Reaction Path

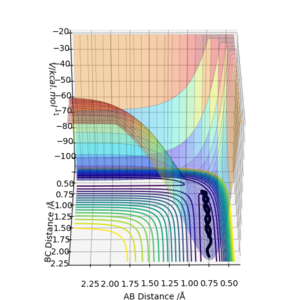
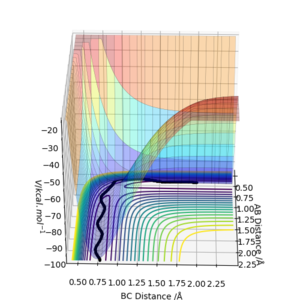
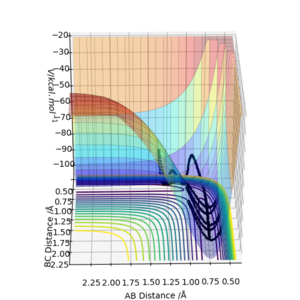
An MEP and dynamic reaction path differ because in the dynamic reaction path the molecules involved have velocities and momenta, but in a MEP the molecule shows the path the molecule would follow if it had no momentum or velocity. The difference in these paths can be seen where the interatomic distances are offset from the transition state by a small amount. In figures 2 and 3 the interatomic distances are set to r_AB=0.9181A and r_BC=0.9081A.

Figure 2: The MEP of the H + H₂ system following a small displacement of r_AB from r_ts

Figure 3: Potential energy surface showing the reaction path of the H + H₂ system when the interatomic distance is displaced from r_ts, in dynamic mode.

In figures 2 and 3 there is a notable difference between the two paths, despite both starting at the same interatomic separations. In figure 3, the reaction trajectory shows that atoms B and C oscillate, but in the MEP trajectory, there is no oscillation.

Reactive and Unreactive Trajectories

Table showing the reactivity and dynamics of reactions with different initial momenta

p1	p2	Etot	Reactive?	Description of dynamics
-1.25	-2.5	-99.018	Yes	Initially molecule AB is not oscillating and is moving slowly towards atom C which is moving towards AB. When they collide, atom B is transferred onto atom C and atom A reverses its direction. Molecule BC moves in the opposite direction to A, and it also oscillates.
-1.5	-2.0	-100.456	No	Trajectory2hb3017.png Molecule AB is initially oscillating and moving towards C and molecule is moving towards AB. When AB and C get close to each other, they both reverse direction and AB continues to oscillate.
-1.5	-2.5	-98.956	Yes	Molecule AB is initially oscillating and AB and C are moving towards each other. When they collide, the reaction occurs and atom A reverses its direction and molecule BC moves off in the opposite direction, whilst oscillating.
-2.5	-5.0	-84.956	No	Molecule AB does not oscillate initially but the interatomic distance between A and B increases slightly whilst they move towards atom C and C moves towards them. When AB and C collide, A moves off slowly in the opposite direction and Band C join to form a molecule which oscillates twice before B rejoins atom A, forming AB which oscillates. AB and C move off in opposite directions.
-2.5	-5.2	-83.416	Yes	Molecule AB and atom C collide and atom B is transferred to C where it starts to oscillate and is transferred back onto molecule A. Once on molecule A, AB oscillates once and B is transferred back onto molecule C where it continues to oscillate. After the collision atoms A and C reverse their direction.

It can be concluded from the table that the reactivity of the system is not solely dependent on the kinetic energy of the molecules. This is evident because the situation with the lowest kinetic energy results in a reaction, but as the initial momentum of the molecules is increased, thus increasing the kinetic energy, the reactions do not always occur. There must be another factor affecting whether the reaction occurs.

Transition State Theory

There are three main assumptions in transition state theory¹:

1) Quantum tunnelling affects are assumed to be negligable and the Born-Oppenheimer is used.

2) The atoms in the reactant have Boltzmann distributed energies.

3)Once the system reaches the transition state with a velocity towards the product, the system will not return to the initial state region during the rest of the reaction. all correct, well done for referencing. Pu12 (talk) 22:12, 16 May 2019 (BST)

The transition state theory states that the rate constant of an elementary reaction can be found using the following equation¹:

     kTS = pTS·rc,TS where pTS is the probability of finding the system in the transition state region and rc,TS is the rate by which the transition state is crossed.

It can be seen from the final row of the table above that the Transition State Theory fails for some reaction trajectories. This is because the system goes through the transition state multiple times as molecule B is transferred from A to C to A to C again. The system must pass through the transition state multiple times, suggesting that assumption 3 breaks down. Since the molecule passes through the transition state multiple times, the probability of being in the transition state is actually higher than the transition state theory would suggest, thus making the reaction rate higher too.

F-H-H System

PES Inspection

Figure 4: The Potential energy surface for the F-H-H system

The potential energy surface(PES) for the F-H-H system can be seen in figure 5. The PES can be used to look at the energetics of the following two reactions: F + H₂ → HF + H and H + HF → H₂ + F. When H and F are bonded, (i.e the AB interatomic distance is constant) the potential energy of the system is very low. However, when H and H are a molecule (i.e. the BC interatomic distance is constant) the potential energy of the system is much higher. For F + H₂ → HF + H, the reaction is exothermic because the systems potential energy for HF is lower than for H₂, so energy is lost from the system as a result of the reaction. This must be lost as heat, making it an exothermic reaction. The H + HF reaction is endothermic because the potential energy of the system for H₂ is significantly higher than that for HF, so energy needs to be taken in for the bond to form.

This can be related to the bond strengths of HF and H₂ too. HF has a bond strength of 565 kJmol^-1 and H₂ has a bond strength of 432 kJmol^-1. Bond breaking is an endothermic process and bond making is exothermic. For F + H₂, a stronger bond is made than is broken, so energy is released in this process, making it exothermic. The opposite is true for HF + H, making the reaction endothermic. On the PES when the system consists of the weaker bonds, the potential energy surface is higher because the system is not as energetically stable as when the strongest bond is formed.

Transition State

Figure 5: A graph of interatomic distance v time when the F-H-H system is in the transition state

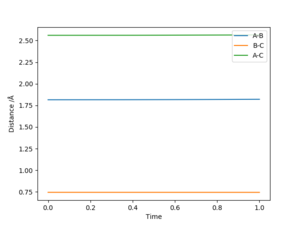
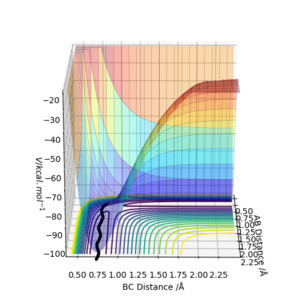
The position of the of the atoms in the transition state, r_ts for the F-H-H can be found in a similar way to the H-H-H system, but instead of having AB and BC distances equal, they are different since the system is not symmetrical. The position of the transitions state was found to be at r_AB = 1.815A and r_BC = 0.745A. Figure 5 shows how the interatomic distance varies with time when the initial conditions are set for r_TS and p=0. The fact that the interatomic distance is constant suggests there is no gradient at that point, meaning it is the transition state.

Activation Energy

Figure 6: A graph showing the energy of an mep throughout the course of the trajectory.

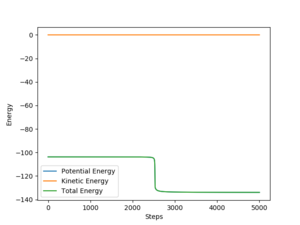
The activation energy for the HF + H and F + H₂ can be approximated by offsetting the interatomic separations slightly from the transition state separations and then running the mep for the reaction with the initial momentum as zero.

In finding the activation energy for HF + H the interatomic separations were set to r_AB=1.80A and r_BC=0.745A. Figure 6 shows a plot of energy v steps for these initial conditions. There is a very evident step in potential energy at about 2500 steps. The size of this step can be approximated as the activation energy for the reaction. This gives an activation energy value of 29.9 kJmol^-1. The activation energy of the reverse reaction can be found by subtracting the potential energy associated with having an H₂ molecule from the energy of the transition state. The calculation is as follows: E_AE(F+H2) = -103.752 - (-103.922) = 0.17 kJmol^-1.

all correct, but energies are given in the program as kcalmol^-1 not kJmol^-1, it doesn't look like you did a conversion. Pu12 (talk) 22:12, 16 May 2019 (BST)

Reaction Dynamics

Figure 7: A momenta v time graph for a successful reaction of F + H₂.

A set of reaction conditions for the F-H-H system that result in a reaction are r_AB=2, r_BC=0.74, p_AB=-3 and p_BC=-7. Figure 7 shows how the momentum of r_AB and r_BC changes before, during and after the reaction. Momentum is conserved in this reaction, meaning that kinetic energy is also conserved. Since the potential of the products is lower than the reactants, the excess energy in this reaction will be lost as heat. The amount thermal energy formed in this reaction could be measured using calorimetry.

Unfortunately you have missed the final question about Polanyi's rules. Otherwise this is a high quality report with only minor mistakes.Pu12 (talk) 22:12, 16 May 2019 (BST)

References

(1) T. Bligaard, J.K. Nørskov, in Chemical Bonding at Surfaces and Interfaces, 2008, 255-321