MRD:01546737
EXERCISE 1: H + H2 system
Dynamics from the transition state region
Defining the Transition State
The transition state is mathematically defined on a potential energy surface as the point where the gradient of the potential is equivalent to zero, i.e. ∂V(ri)/∂ri=0. It is a saddle point, and lies on the minimum energy path between reactants and products. It can be easily identified if trajectories are started near the transition state. If the transition state is present, then the trajectory will 'roll' in the direction of either the reactants or the products, whereas if a local energy minima is present, then the trajectory may become stuck in a potential well and will not 'roll' towards the reactants or products.
The transition state and local potential minima can be further distinguished by looking at the Hessian matrix for the point. For an energy minima, then it would be expected that overall the dot product of the eigenvalues and orthogonal eigenvectors would lead to both vectors being positive, i.e. going up the 'slope' of the potential surface, whereas at the transition state, on the saddle point, one of the vectors would be positive, going 'up the slope', and the other would be negative, going 'down the slope'. Good. Pu12 (talk) 17:04, 21 May 2020 (BST)
Locating the Transition State Using r1=r2
Using r1=r2 and p1=p2=0, the transition state position, rts was found to be located at 90.77pm. This is clearly shown in the internuclear distances vs time graph for this position, as the gradients for A-B, B-C and A-C are all equivalent to 0, showing that at this location the atoms exhibit no oscillation along the ridge or r1=r2. This will occur when there is no force acting upon the atoms. One definition of force is the variation of momentum, or mathematically ∂Pi/∂t . This partial derivative is equal to -∂V(r1,r2,...)/∂ri, and as we have previously discussed at the transition state this is equal to zero. As such at the transition state, no force will be acting on the atoms, meaning that they will not oscillate.
Trajectories from r1+δ, r2
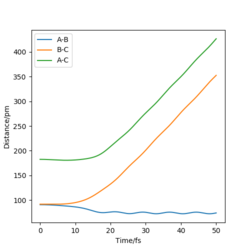
Through a comparison of the trajectory from contour plots created from the MEP and Dynamics calculations, it is clear that the trajectory follows the minimum energy path in the MEP calculation, whilst oscillation occurs in the Dynamics trajectory. This is because in the MEP calculation, there is an infinite 'friction' acting on the trajectory, meaning that as it 'rolls', it is not able to pick up any momentum, and therefore no net force acts on the system. In contrast, the Dynamics calculation is an accurate representation of the system, and therefore means that momentum is allowed to build up as it 'rolls' towards the products, applying a force on the atoms in the system, in turn causing them to oscillate.
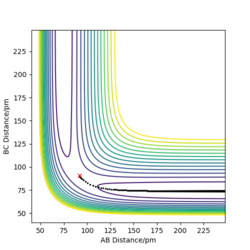
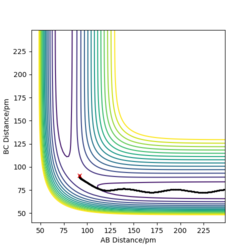
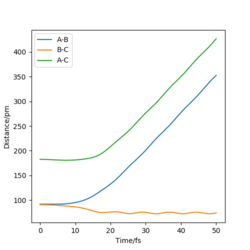
The following plots are for the compare the 'Internuclear Distances vs Time' plots and 'Momenta vs Time' plots for the system previously described and the system r1=rts, r2=rts+δ, using the Dynamics calculation for both. It is clear that both graphs look identical, however in the second system the lines representing A-B and B-C have been swapped. This is because the change in displacement in the second system means a change in trajectory as the system 'rolls' towards a different set of products, HA + HB-HC.
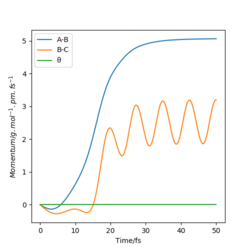
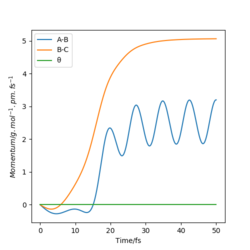
The following graphs correspond to a system where the initial positions are the final positions of the r1=rts, r2=rts+δ, and the initial momenta is the negative of the final momenta from the previous system. It is observed that the trajectory of the system is reversed, and the system returns to the initial conditions of r1=rts+δ, r2=rts.
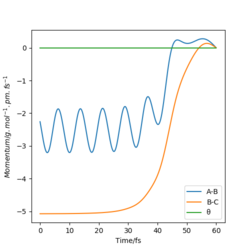
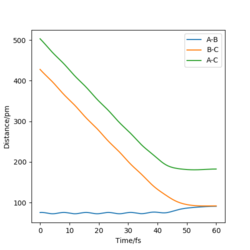
Reactive and Unreactive Trajectories
Table of Varying Trajectories
| p1/g.mol-1.pm.fs-1 | p2/g.mol-1.pm.fs-1 | Etot/KJ.mol-1 | Reactive? | Description of Dynamics | Illustration of the Trajectory |
|---|---|---|---|---|---|
| -2.56 | -5.1 | -414.280 | yes | The system has sufficient energy to overcome the saddle point, after which the atoms continue along the trajectory with some oscillation. | 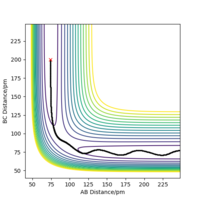 |
| -3.1 | -4.1 | -420.077 | no | This system has a lower total energy than the previous one, and therefore does not have sufficient energy to overcome the saddle point, meaning that it is unreactive, and the trajectory travels back towards the reactants. |  |
| -3.1 | -5.1 | -413.977 | yes | Similarly to the first trajectory, the system is able to overcome the saddle point, however the fact that there is more energy in the system means that when 'rolling' towards the products, there is greater oscillation. |  |
| -5.1 | -10.1 | -357.277 | yes | This trajectory is an example of barrier recrossing. Due to the sufficient energy in the system, after the products are formed, the trajectory 'rolls' back over the saddle point towards the reactants Barrier recrossing doesn't count as a reactive trajectory. Pu12 (talk) 17:55, 21 May 2020 (BST) |  |
| -5.1 | -10.6 | -349.477 | yes | This trajectory has the greatest total energy. After some oscillation of the atoms about the saddle point, the trajectory crosses over and 'rolls' towards the products with the greatest oscillation of any of the trajectories due to the greatest total energy. | 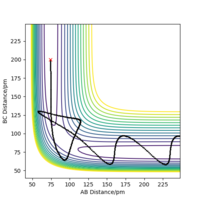 |
Should have a brief explanation of what the table shows, e.g that you need not only enough energy for the reaction to go, but also the correct balance of translational/vibrational energies. Pu12 (talk) 17:04, 21 May 2020 (BST)
Transition State Theory
Transition State Theory will overestimate the rate of reaction in comparison to experimental values. One of the conditions for Transition State Theory is that once the system has crossed over the potential energy barrier and is 'rolling' towards the products, it is not able to cross the saddle point again and therefore the system cannot revert back to the products. In reality however, barrier recrossing can occur, as shown in the fourth trajectory of the previous table, meaning that experimentally not all trajectories that cross over the transition state saddle point will lead to the formation of the products, slowing down the overall rate of reaction. Good. Pu12 (talk) 17:04, 21 May 2020 (BST)
EXERCISE 2: F-H-H system
PES Inspection
Energetics of the F + H2 and H + HF reactions
The F+ H2 reaction is exothermic as, according to Hammond's postulate, for an exothermic reaction, the transition state will lie close to the reactants and will therefore resemble said reactants. In contrast, the H + HF reaction is endothermic as the transition state lies close to the products, and will in turn resemble the products. These reaction energetics directly relate to the H-F and H-H bond strengths. The F-H bond is stronger than the H-H bond, and as such the formation of the H-F bond is overall exothermic as there is a net energy release caused by the formation of a strong bond. The H-H bond formation from H-F + H is endothermic as there is a net energy loss, because the strong H-F bond must be broken.
The Approximate Position of the Transition State
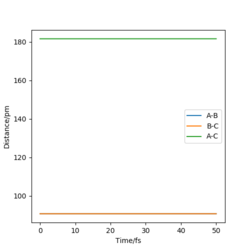
The transition state of the H-H-F system lies approximately at H-F = 181.28 pm and H-H = 74.15 pm. A change of δ= ±1 pm on either of the bond distances changes the trajectory in the direction of either the reactants or the product. In addition, the internuclear distances - time graph shows that the bond lengths exhibit only slight oscillation when the trajectory starts at this point, and are practically constant. This in turns means that very little force is acting on the atoms at these positions, suggesting that they are very close to the transition state position. Furthermore, the orthogonal vectors formed from the Hessian matrix of this point show one 'going up' the wall of the potential energy slope, whilst the other is 'pointing down' the slope towards the products, suggesting that it lies very close to the saddle point.
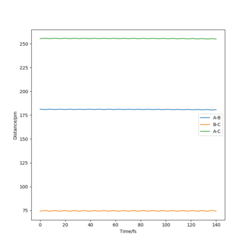

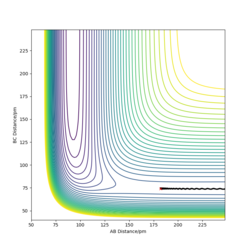
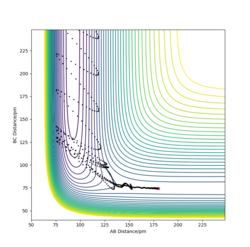
Good, a contour/surface plot can be used to demonstrate this. Pu12 (talk) 17:04, 21 May 2020 (BST)
Activation Energy for H2 + F and HF + H reactions
The activation energy for the formation of H2 was calculated to be 126.624 KJ.mol-1, whilst the activation energy for the formation of H-F was found to be 0.938 KJ.mol-1. These were found by performing an MEP reaction that started from a slight deviation from the transition state position, and the difference between the saddle point energy and energies of reactants for the system were taken using energy vs time plots.

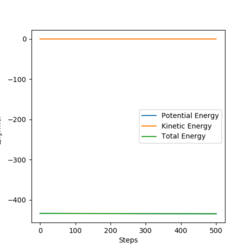
Correct. Pu12 (talk) 17:04, 21 May 2020 (BST)
Reaction Dynamics
The Release of Reaction Energy
Upon inspection of a momenta-time graph for a successful reaction for the formation of H-F from H2, upon the formation of the product, there is greater vibrational energy in the H-F bond, in comparison to the H-H bond of the H2 reactant. This is because there is a large release of potential energy from the reactants, which is in turn converted to kinetic energy, primarily in the form of vibrational energy in the products. This vibrational energy in turn increases the overall heat energy present in the system. There is therefore an increase in temperature of the system. This change in temperature can be measured experimentally using a calorimeter. The heat released from the exothermic reaction is transferred to the solution in the calorimeter, with the change in temperature of solution being calculated by the equipment.
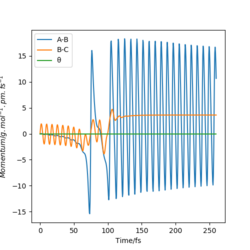
Distribution of Energy in the System
For a system starting with the reactants F + H2, with the initial conditions rHH= 74 pm, rHF=200 pFH= -1.0 g.mol-1.pm.fs-1, a range of values for pHH were investigated, between -6.1 to 6.1 g.mol-1.pm.fs-1. It was observed that the negative pHH had overall less vibrational kinetic energy to begin with than a positive value of the same magnitude. It was also observed that because the system had a lot greater energy in the form of initial vibrational energy, system recrossing could sometimes occur. When system recrossing occured, the H2 molecule was observed to travel away from F with less vibrational and translational kinetic energy than when approaching F. However when the reaction was successful, HF had much greater vibrational energy than the H2 reactant, and both products had more translational energy. This shows that if system recrossing occurs, then there is a net gain in potential energy, due to some kinetic energy being used to overcome the small initial activation energy in the first crossing.
When the overall energy of the system is significantly reduced by changing pFH to -1.6 g.mol-1.pm.fs-1, and pHH to 0.2 g.mol-1.pm.fs-1, the system still has enough energy to overcome the initial activation energy barrier, however there is not sufficient energy for system recrossing to happen, meaning that overall there is a formation of F-H, and again a release of kinetic energy to the system, primarily in the form of translational and vibrational energy.
Though the inversion of momentum procedure was used, a reactive trajectory that successfully achieved the formation of H2 from HF + H was not found. However in the process of trying to find such a reactive trajectory, it was observed that a higher vibrational energy of the reactants is much more important to the success and efficiency of a reaction than high translational energy. This is because the trajectory of the reactants is already oscillating about the potential well, so therefore less external energy (in the form of translational energy) is required to overcome the saddle point than if the molecules were residing at the bottom of the potential well. If the position of the transition state were more central between the products and the reactants, then overall for an endothermic reaction, as in this example, it would resemble the products less and would in turn require less potential energy to be overcome. This would mean that the reaction rate would be less dependent on the vibrational energy possessed by the reactants, and translational energy of reactants would have more of an effect in determining whether a reaction is successful. I am not sure what you are trying to say here, the potential energy that must be overcome can be overcome both by vibrational and translational energy. Pu12 (talk) 17:04, 21 May 2020 (BST)
This explanation is a little confusing, however you do predict the correct relationship between transition state position and need for translational or vibrational energy. It would be beneficial to reference Polanyi's rules in your explanation "For an exothermic reaction - early transition state - energy must be mostly provided in the form of translational energy, whereas for an endothermic reaction - late transition state, energy must be mostly provided in the form of vibrational energy". Pu12 (talk) 17:04, 21 May 2020 (BST)
Overall a good report, you show understanding throughout. Pu12 (talk) 17:04, 21 May 2020 (BST)
You should include some references for where you got information from, for example in the first question where you discuss eigenvalues. Pu12 (talk) 20:45, 21 May 2020 (BST)
