MRD:01531254

Molecular Reaction Dynamics Lab

The objectives of this exercise are to study the reactivity of triatomic systems, where an atom and a diatomic molecule collide, through calculating Molecular Dynamics trajectories.

Exercise 1: H + H₂ system

Dynamics from the transition state region

On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?

The transition state is defined as the maximum on the minimum energy path linking reactants and the products. The transition point can be identified on a potential energy surface as being at a saddle point, where the reactive trajectory is at its highest point and the gradient of the potential energy surface is zero. Saddle points have a local maximum in one direction and a local minimum in the other. They can be mathematically defined using their gradient: the partial derivative of the gradient, f_x, equals zero, indicating that the gradient is zero at this point. Furthermore, saddle points are distinguished from local minima in that the result of the second partial derivative test, f_xxf_yy-f_xy², is larger than zero.

A PES with the transition state region highlighted.

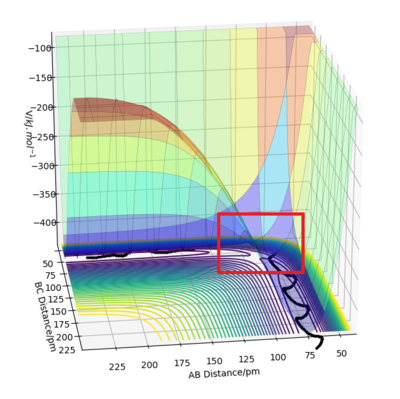
Good description. Details on you image (ie highlighted region) or refering to image in your description would be a great addition. Also, when referencing, try to reference the primary source or close to the primary source. Khan academy is not a good reference. Sf3014 (talk) 12:08, 18 May 2020 (BST)

Trajectories from r₁ = r₂: locating the transition state

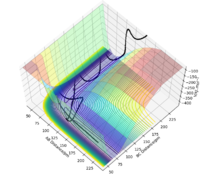
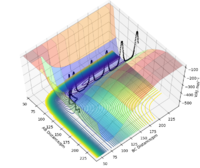
Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

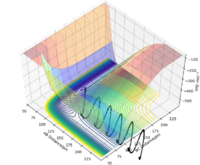
Since the H + H₂ surface is symmetric, the transition state must have r₁ = r₂. In trajectories from r₁ = r₂ the trajectory oscillates on the ridge; this can be used to locate the transition state geometry.

When testing different initial conditions with r₁ = r₂, and p₁ = p₂ = 0.0 g.mol^-1.pm.fs^-1, it can be seen that the system undergoes a periodic symmetric vibration.

For example, the Internuclear Distances vs Time plot for r₁ = r₂ = 100 pm , p₁ = p₂ = 0.0 g.mol^-1.pm.fs^-1 is shown below ,and clear oscillation can be seen.

The Internuclear Distances vs Time plot for r₁ = r₂ = 100 pm.

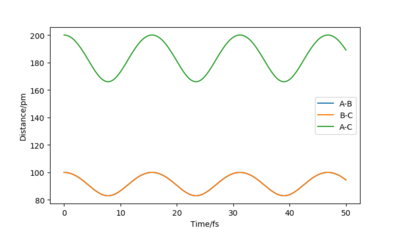
However, when r₁ = r₂ is set to 91, the vibration is very minimal. This is a good estimate for the transition state because when a trajectory starts at the transition state, with no initial momentum, it stays there forever.

The Internuclear Distances vs Time plot for r₁ = r₂ = 91 pm.

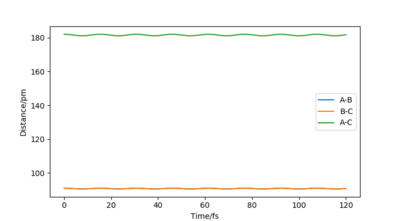
Description easy to follow, but units missing for transition state position. Also, the position can be more accurate Sf3014 (talk) 13:05, 18 May 2020 (BST)

Calculating the reaction path and trajectories from r₁ = r_ts+δ, r₂ = r_ts

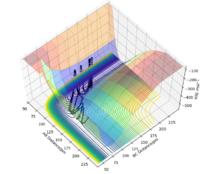
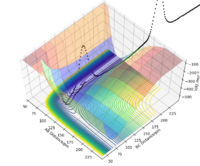
Comment on how the mep and the trajectory differ.

The minimum energy path (or mep) is a very special trajectory that corresponds to infinitely slow motion. This can be tested with initial conditions r₁ = r_ts + 1 and r₁ = r_ts, and p₁ = p₂ = 0.0 g.mol^-1.pm.fs^-1 and the calculation type as 'MEP'. With r₁ set at 92 and r₂ set at 91, it can be seen that the trajectory simply follows the valley floor to H₁ + H₂ - H₃. Good, but refer to highlighted region on image in your description. Also why does the trajectory "follow the valley floor"? Sf3014 (talk) 12:37, 18 May 2020 (BST)

A PES with the mep trajectory highlighted.

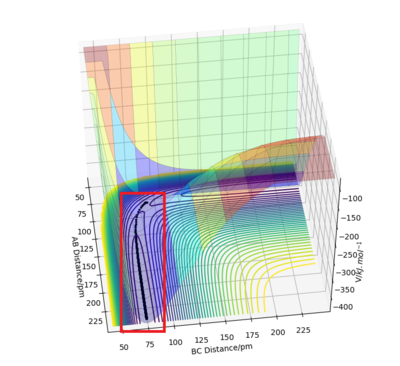
However, mep doesn't provide a realistic account of the motion of atoms during a reaction because it doesn't account for the mass of the atoms. When the same reaction is repeated with the calculation type as 'Dynamics' rather than 'MEP', the inertial motion of the atoms is indicated by the oscillation of the BC distance caused by the masses interacting. Yes, the mep calculation approximates for no vibrational energy. However, your conclusion is not clear because the oscillations are also proportional to bond strength. Sf3014 (talk) 12:37, 18 May 2020 (BST)

A PES with the reaction path highlighted.

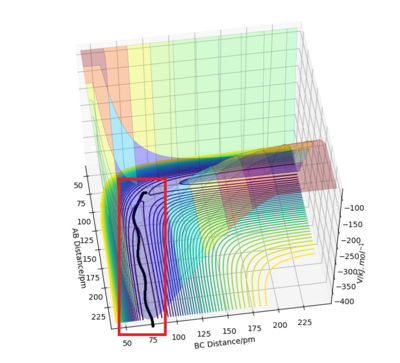
Reactive and unreactive trajectories

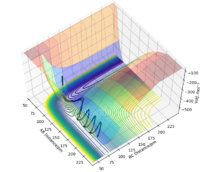
Complete the table by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?

Initial positions r₁ = 74 pm and r₂ = 200 pm:

p1 / g.mol-1.pm.fs-1	p2 / g.mol-1.pm.fs-1	Etot / kJ.mol-1	Reactive?	Description of the dynamics	Illustration of the trajectory
-2.56	-5.1	-414.280	Yes	m1 and m2-m3 collide and react to form m1-m2 and m3
-3.1	-4.1	-420.077	No	m1 and m2-m3 do not collide so no reaction occurs
-3.1	-5.1	-413.977	Yes	m1 and m2-m3 collide and react to form m1-m2 and m3
-5.1	-10.1	-357.277	No	m1 and m2-m3 collide and r1 oscillates but m2-m3 remains intact so no reaction occurs. This is a case of barrier recrossing: the system crosses the transition state region, the bond in the product forms, but then the system reverts back to the reactants.
-5.1	-10.6	-349.477	Yes	m1 and m2-m3 collide, and though r2 oscillates they ultimately react to form m1-m2 and m3

Good layout and descriptions. What can you conclude from this table? Sf3014 (talk) 13:06, 18 May 2020 (BST)

Transition State Theory

Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

A powerful theory to rationalise and calculate the rate of chemical reactions based on the properties of the reactants and the transitions state structure is Transition State Theory. It predicts that the rate constant for a generic bimolecular reaction ${𝒜}{+}{ℬ}\to {𝒫}$ is:

$k_{TST}=R_{cl}\frac{{Q_{{‡}^{\prime }}}^{\prime }/V}{(Q_{{𝒜}}/V)(Q_{{ℬ}}/V)}{e}^{-\frac{E_0}{k_{B}T}}$

A crucial assumption of Transition State Theory in estimating R_cl is that all trajectories with a kinetic energy along the reaction coordinate greater than the activation energy will be reactive. By further assuming that the kinetic energy along the reaction coordinate follows the Boltzmann distribution, one obtain the conventional Transition State Theory rate constant expression:

$k_{TST}=\frac{k_{B}T}{h}\frac{{Q_{{‡}^{\prime }}}^{\prime }/V}{(Q_{{𝒜}}/V)(Q_{{ℬ}}/V)}{e}^{-\frac{E_0}{k_{B}T}}$

In Transition State Theory motion is treated by classical mechanics, and it is assumed that this motion always leads to products without recrossings of the saddle point. This is incorrect as quantum mechanical tunneling allows barrier crossing to take place when the total energy is less than the potential energy at the top of the barrier. Barrier recrossing is seento occur in the calculated experiment values, for example:

The PES of a reaction where barrier crossing occurs.

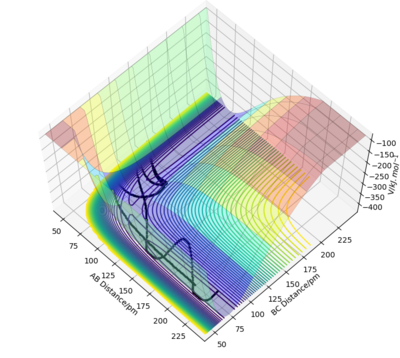
Good description and use of reference. Missing in description, how does TST effect the rate of reaction compared to experimental values? Sf3014 (talk) 13:20, 18 May 2020 (BST)

Also, when using equations, variables should be defined Sf3014 (talk) 13:23, 18 May 2020 (BST)

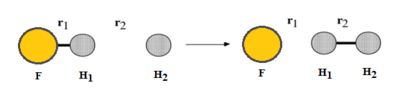
Exercise 2: F - H - H system

PES inspection: F + H₂

By inspecting the potential energy surfaces, classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved? Locate the approximate position of the transition state. Report the activation energy for both reactions.

F + H₂ is an exothermic reaction as characterised by the fact that the transition state occurs early in the reaction coordinate on its potential energy surface, i.e. it is an attractive surface. This relates to the bond strengths involved as a relatively weak H-H bond is broken while a strong H-F bond is formed; bond making is an exothermic process, so the formation of a bond with high bond enthalpy makes the overall reaction exothermic.

The contour plot of F + H₂ with the transition state region highlighted.

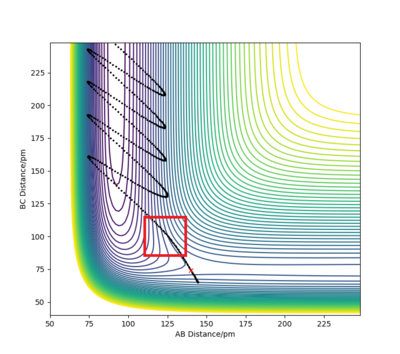
The approximate position of the transition state is where the F---H gap is 125 pm and the H---H gap is 96 pm. This is reflected in the Internuclear Distances vs Time plot where this position is set at this position with p₁ = p₂ = 0.0 g.mol^-1.pm.fs^-1; the system undergoes a periodic symmetric vibration but does not move from the spot. This structure is consistent with Hammond's postulate, where the transition state in an exothermic reaction is close in structure to the reactants.

The Internuclear Distances vs Time plot of F + H₂ at the position r₁ = 125 pm and r₂ = 96 pm.

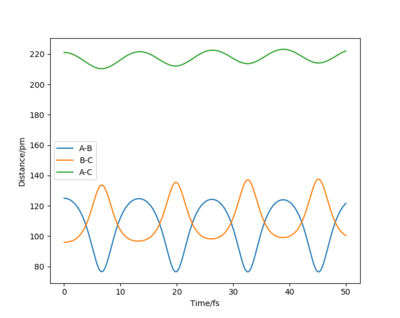
Part of the Energy vs Time plot is shown from the reaction, depicting the potential energy of the products, transition states and reactants. From this the activation energy can be calculated to be 59 kJ/mol for this reaction. note:the activation energy is a bit too high Sf3014 (talk) 21:45, 18 May 2020 (BST)

The beginning of the Energy vs Time plot of F + H₂.

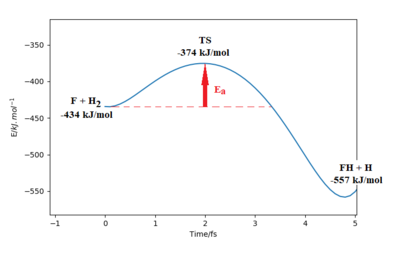
PES inspection: H + HF

By inspecting the potential energy surfaces, classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved? Locate the approximate position of the transition state. Report the activation energy for both reactions.

H + HF is an endothermic reaction as characterised by the fact that the transition state occurs late in the reaction coordinate on its potential energy surface, i.e. it is an repulsive surface. This relates to the bond strengths involved as a strong H-F bond is broken while a weaker H-H bond is formed; bond breaking is an endothermic process, so the breakage of a bond with high bond enthalpy makes the overall reaction endothermic. Good but show energies of reactions using an image of the potential energy surfaces and refer to it in your descriptions for H + HF and F + HH. Also, you can back up your information on H-F and H-H bond energies using their bond energies Sf3014 (talk) 13:36, 18 May 2020 (BST)

The contour plot of H + HF with the transition state region highlighted.

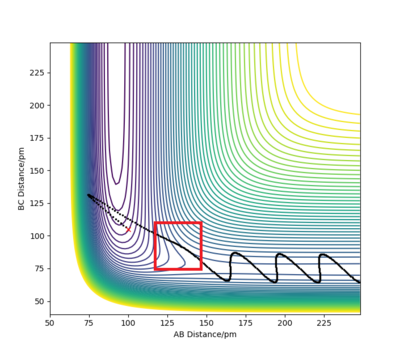
The approximate position of the transition state is where the F---H gap is 125 pm and the H---H gap is 96 pm. This is reflected in the Internuclear Distances vs Time plot where this position is set at this position with p₁ = p₂ = 0.0 g.mol^-1.pm.fs^-1; the system undergoes a periodic symmetric vibration but does not move from the spot. This structure is consistent with Hammond's postulate, where the transition state in an endothermic reaction is close in structure to the products.

The Internuclear Distances vs Time plot of H + HF at the position r₁ = 129 pm and r₂ = 90 pm.

Part of the Energy vs Time plot is shown from the reaction, depicting the potential energy of the products, transition states and reactants. From this the activation energy can be calculated to be 160 kJ/mol for this reaction.

The beginning of the Energy vs Time plot of H + HF.

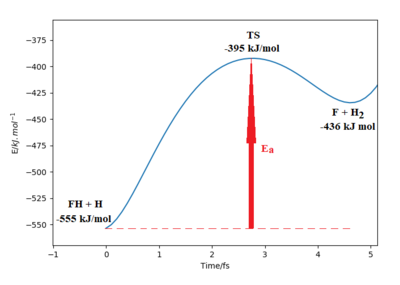
Good descriptions on finding TS. Need to refer to highlighted region on image. Also, more description needed on the activation energy value, how was the activation energy calculated? Sf3014 (talk) 13:43, 18 May 2020 (BST)

Reaction dynamics: F + H₂

In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.

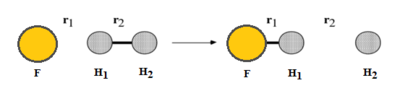
One set of initial conditions that results in a reactive trajectory for F + H₂ is r₁ = 140 pm, r₂ = 74 pm, p₁ = 0 g.mol^-1.pm.fs^-1 and p₂ = -5 g.mol^-1.pm.fs^-1. By considering the animation and Momenta vs Time plot, the mechanism can be examined. As H₂ approaches F the momentum of its bond increases; after the transition state, where H₁ bonds with F and the other H moves away from the new product, the H-F bond oscillates.

The Momenta vs Time plot of F + H₂.

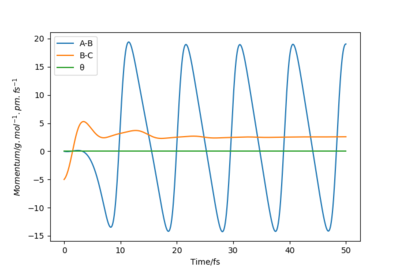
The hydrogen molecule could be polaried by the electronegative fluoride and form a bond in the transition state via an S_N2 mechanism. It could be possible to determine the order of the reaction experimentally, which should correspond to a S_N2 rate law involving the concentrations of both the species in the reaction. Description is unclear as to how energy is conserved. No mention of energy transfer and how the total energy remains constant. You need to refer to your images. Also answer is incomplete, how can you confirm the conservation of energy experimentally? provide experiment and description Sf3014 (talk) 13:56, 18 May 2020 (BST)

Reaction dynamics: Polanyi

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Polanyi's empirical rules explain and predict the effect of translational and vibrational energy in driving reactions. They state that for reactions with an early transition state / reactant-like transition state, translational energy is most effective in driving the reaction; for reactions with a late transition state / product-like transition state, vibrational energy is most effective in driving the reaction. These rules can be demonstated through different case studies: F + H₂ falls into the first category, so is most affected by translational energy, and H + HF falls into the second category, so is most affected by vibrational energy. Consider the following examples:

rFH	rHH	pFH	pHH	Description	Diagram
160	74	-1	-6.1	The H2 molecule has a high amount of energy on the H-H vibration. The system undergoes barrier recrossing but does not react because for systems with an early transition state translational energy is more effective.
160	74	-1	6.1	The H2 molecule has a high amount of energy on the H-H vibration. The system undergoes barrier recrossing but does not react because for systems with an early transition state translational energy is more effective.
160	74	-1.6	0.2	The H2 molecule has a low amount of vibrational energy. The system reacts successfully because for systems with an early transition state translational energy is more effective.
94	150	0	21	The HF molecule has a low amount of vibrational energy. The system molecules collide but do not react successfully because for systems with a late transition state vibrational energy is more effective.
94	150	21	0	The HF molecule has a high amount of energy on the H-F vibration. The molecules collide and react successfully because for systems with a late transition state vibrational energy is more effective.

Good but more how does the energies (vibrational and translational) relate to the initial conditions of momenta? Sf3014 (talk) 14:08, 18 May 2020 (BST)