MRD:01504509
Molecular Reaction Dynamics: Applications to Triatomic systems
General remarks: Please do get in the habit of defining all your quantities (What is V? what is A,B,C?), giving proper references, and also labelling and referencing your Figures (i.e. adding a caption with e.g. 'Figure 1', but also referring to every figure in the text). Sometimes you have mentioned, e.g. 'figure 1' in the text, but the figures are not labelled, so I cannot assign them. Fdp18 (talk) 08:20, 27 May 2020 (BST)
There are some important issues with understanding, see the comments below. In some cases I think you understood the concepts, but were not able to articulate your thoughts in a clear and concise way. I recommend that, when you're finished with a report, you give it to a peer/family member/... to read over, it can be as simple as deleting a repeated work that makes one stumble over a sentence. Fdp18 (talk) 08:58, 27 May 2020 (BST)
EXERCISE 1: H + H2 system
Question 1
On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
answer

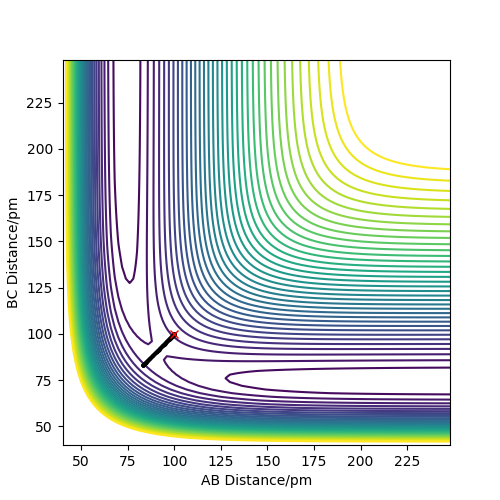
On the PES (Potential Energy Surface) diagram, the transition state has the highest potential energy That is not correct - just take a look at the PES: there are many points with higher energy, and in the 3D surface you even clipped some. Fdp18 (talk) 08:15, 27 May 2020 (BST)
and is represented by the saddle point thus the gradient is zero (∂V(ri)/∂ri=0) as the maximum point in one direction, or we say it is a minimum along with the symmetric stretch coordinates, but a maximum along the asymmetric stretching coordinates. Although the saddle points mean that the gradient/slope is zero which can represent both local maximum and minimum, this can be distinguished by its second derivative since the second derivative at the point of the transition state(maximum) will be a negative value (negative curvature) while for the local minima, it is a positive value (positive curvature). That is correct - but how do you use the second derivatives to define the saddle point? You only defined local maxima and minima so far. Fdp18 (talk) 08:17, 27 May 2020 (BST)
Question 2
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a“Internuclear Distances vs Time” plot for a relevant trajectory.
answer



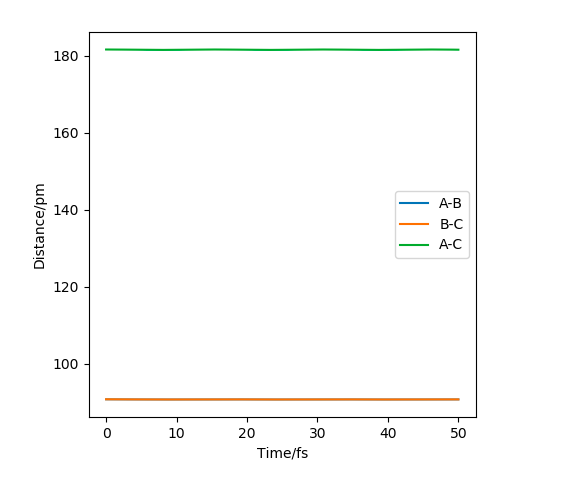
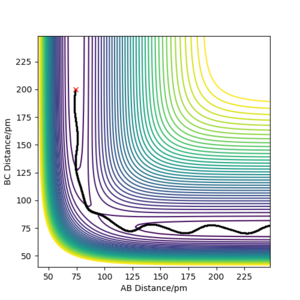
The estimate of the transition state position should be about 90.8pm. H-H-H should be the transition state as a triatomic molecule since it shows the highest energy. For the initial conditions, the distance r1=r2=100pm(figure 2), The trajectory shows periodic symmetric vibrations(oscillations), but it might fall off What do you mean by "fall off"? Fdp18 (talk) 08:18, 27 May 2020 (BST)
if the motion is slight. As can be seen from the three plots, when r=91pm, the three atoms are stationary. At r=100.8pm or r=80.9pm, the three atoms move to the greatest amplitude spending similar times. When the distance decreases to 80pm(figure 2), we can see that the atoms will first get further; When the distance increases(to 120pm), the atoms will first get closer(figure 3) all of which shows that the transition state (triatomic molecule) will be formed at a position of r=91pm and the trajectory formed will not fall off since the slope is zero at this stationary point. I assume you mean "fall off the transition state". While you can imagine the PES like a landscape, you should aware that this is only to help you understand it - the atoms do not "move in this valley". Fdp18 (talk) 08:23, 27 May 2020 (BST)
Question 3
Comment on how the mep and the trajectory you just calculated differ.
answer
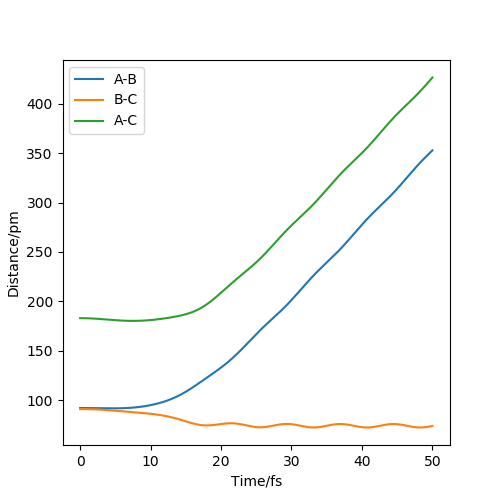
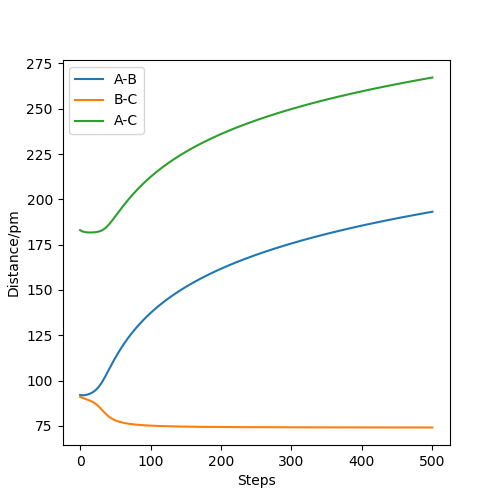
The two graphs show a minimum energy pathway (MEP) and a dynamic trajectory with the same distance condition: r1 = 92pm, r2 = 91pm and the momenta p1 = p2 = 0 g.mol-1.pm.fs-1. The MEP describes infinitely slow motion which has the property that any point on the path is at an energy minimum in all directions perpendicular to the path. This path passes through at least one first-order saddle point. The MEP can also be described as the union of steepest descent paths from the saddle points to the minima. For Figure 1, MEP shows that distance B-C decreases, while distance A-B increases at the pattern as that of distance A-C with a decreasing gradient and eventually reaches velocity zero. For Figure 2, Dynamic shows that the distance B-C keeps oscillating showing the oscillations of the atoms. Distance A-B is almost constant at first but increases sharply later on. Since the velocity is zero as we concluded in MEP, the momentum and kinetic energy will also be zero( p=mv and KE=1/2mv^2). Along with the increase of the distance B-C compared with the transition state, the reaction pathway will favor the product BC. Thus, if we change the condition to r1 = 91pm, r2 = 92pm, the only change is that the pathway will favor the reactant AB. The directions that atoms move can decide which product will be formed because an opposite sign in the momenta will result in the opposite direction in velocity.
Question 4
Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?
answer
Conclusion:
1. Particles oscillate if they are close together: When they are too close, repulsion occurs; When they move a bit further away, the attraction will then occur, and the higher the KE will result in stronger oscillation.
2. Atoms with energy lower than the activation energy are still able to make the reaction happen(passes the transition state). Think about this carefully. We are simulating in classical mechanics - is what you just described possible? To make such a controversial statement, you need to provide the barrier height and then show that the atoms did not have enough energy to overcome it, but still did. (Which really should not happen) Fdp18 (talk) 08:26, 27 May 2020 (BST)
If the kinetic energy is out of a specific range, the products and reactants will be unstable, which maybe due to the barrier recrossing.
3. The atom at a long distance from the other two atoms experiences no force, thus constant momentum.
In the whole table below, "AC" is never a product (and also not a reactant) - take a look at the right column. Fdp18 (talk) 08:31, 27 May 2020 (BST)
|
p2/ g.mol-1.pm.fs-1 | Etot |
|
Description of the dynamics | Illustration of the trajectory(1) | Illustration of the trajectory(2) | ||
|---|---|---|---|---|---|---|---|---|
| -2.56 | -5.1 | -414.28 | Reactive | The reactive trajectory moves along the reactants BC side, passes the transition state then reaches the product AC side. Carefully look at your trajectories again. The reactants are AB in this case. (applies to other assignments as well) Fdp18 (talk) 08:29, 27 May 2020 (BST)
 |
 |
 | ||
| -3.1 | -4.1 | -420.077 | Unreactive | The reactive trajectory moves along reactants BC side then stops at the TS without reaching the product AB, and comes back to its starting point |
 |
 | ||
| -3.1 | -5.1 | -413.977 | Reactive | The reactive trajectory moves along the reactants BC side, passes the transition state then reaches the product AC side |
 |
 | ||
| -5.1 | -10.1 | -357.277 | Reactive |
 |
 |
 | ||
| -5.1 |
|
-349.477 | Reactive | The reactive trajectory moves along the reactants BC side, passes the transition state(for a few tims) then reaches the product AC side |
 |
 |
Question 5
Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
For systems with different momenta thus kinetic energy, it was thought that only systems with enough energy to overcome the activation energy can proceed to the product. However, the table below with the data for different momenta of the hydrogen molecules and hydrogen atoms has shown that this hypothesis is not appropriate, because we cannot make a conclusion between the reaction pathways and the kinetic energy. For example, in the second row the system Etot is greater than in the first case, however, the reaction trajectory shows that no product is formed and in the 5th row, the system Etot is the lowest of all but still shows a reaction trajectory which passes the transition state and forms product.
OK, I see the problem. This is really important - the 5th row is the one with the highest energy. The values are negative - i.e. the one with the least negative value is the highest. Fdp18 (talk) 08:35, 27 May 2020 (BST)
Transition state theory (TST), instead, can be used to explain the observations in the table below which explains the reaction rates of elementary chemical reactions. The theory assumes a special type of chemical equilibrium (quasi-equilibrium) between reactants and activated transition state complexes.[2]
There are several assumptions for TST:
1. The reactants are in quasi-equilibrium with the transition state
2. Once a reaction has passed the transition state, it cannot reform the reactants
3. The motion of the reaction can be treated classically, ignoring quantum effects such as quantum tunneling
4. Energy is distributed in accordance with the Maxwell-Boltzmann distribution
Another theory is Quantum Tunnelling effect, stating that a subatomic particle's probability disappears from one side of a potential barrier and appears on the other side without any probability current (flow) appearing inside the well. Quantum tunneling is not predicted by the laws of classical mechanics where surmounting a potential barrier requires enough potential energy. In this case, the quantum tunnelling effect contributes more to the energy barrier instead of the rate of reactions. I don't understand this last sentence. Quantum tunneling does not change the barrier, nor does the rate of reactions. Fdp18 (talk) 08:39, 27 May 2020 (BST)
In the 4th and 5th row, the trajectory moves back to the initial state when it passes the transition state, which contradicts TST, thus there is an overestimation of the transition state in these two situations.
be careful not to confuse "transition state" and "reaction rate". The transition state stays the same in all cases, and it doesn't even have to be encountered in a "real" trajectory to be reactive. what is overestimated (by TST) is the reaction rate. Fdp18 (talk) 08:39, 27 May 2020 (BST)
answer
EXERCISE 2: F - H - H system
Question 6
By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
answer:
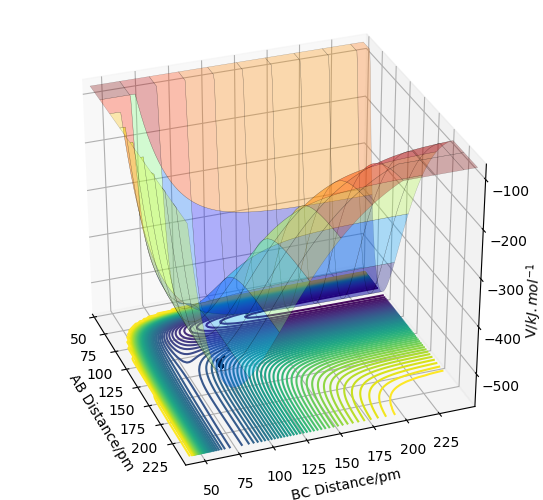
The initial conditions of the PES were set to r1=200 pm and r2=100pm as MEP, showing that when the distance H-F decreases the distance between increases along with the more negative energy. For the formation of HF using F+H2, it should be classified as an exothermic reaction since the energy is released. For H+HF, the distance HF decreases, and the distance between the two H atoms increases, thus relatively higher energy will be needed to break the bond between H and F, making HF + H reaction endothermic. For an exothermic reaction, the energy released during bond formation will be larger than the energy required to break bonds, so the energy released for HF formation is higher than the energy needed to break the H-H bond. For the endothermic, the energy released in the process of the H2 bond formation is less than the energy needed to break the H-F bond. Therefore, the bond strength of HF is stronger than that of H2, this agrees with the experimental values:
ok - however, some sentences are hard to read and understand, especially the first one. Fdp18 (talk) 08:41, 27 May 2020 (BST)
| Bond | Bond length | Bond energy/kJ/mol |
|---|---|---|
| H-H | 74 | 432 |
| H-F | 92 | 565 |
[1]
Question 7
Locate the approximate position of the transition state.
answer

It is clear that the molecule is not symmetric. When we change rAB, no resultant forces will act on the system and the distances between the atoms are constant over time, confirming that transition state has been found. The figure above shows that at the transition state, rAB(HH)=181pm and rBC(HF)=74.5pm, which can be used to determine whichever the reactant or the product the transition state favors. For example, in an exothermic reaction the transition state is closer in energy to the reactants than to the products. Therefore, the transition state will be more geometrically similar to the reactants than to the products. In contrast, however, in an endothermic reaction the transition state is closer in energy to the products than to the reactants. So, according to Hammond’s postulate the structure of the transition state would resemble the products more than the reactants[3], thus the transition state favors H2 and F.
How did you arrive at this value? I'm looking for a description for what you did, similar to the H-H-H case. With the information given above, I could not reproduce your experiment... Fdp18 (talk) 08:43, 27 May 2020 (BST)
Question 8
Report the activation energy for both reactions.
answer



The three figures above show the plot of the energies of reactant(H2+F), product(HF+H), and transition state thus can be used to determine the activation energy. The activation energy is the minimum energy required to overcome for the reaction to happen, thus it is the difference between the potential energy of the transition state and the initial state. Therefore, the activation of the F+H2 reaction is 1.08 KJ mol-1 and the activation energy of HF+H reaction is 126.7KJ mol-1.
Good value and convincing confirmation that the points are stationary, although I still don't see how you arrived there. I know you must have done the right thing because of the values you present, but you need to show what you did. Fdp18 (talk) 08:44, 27 May 2020 (BST)
Question 9
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.
answer
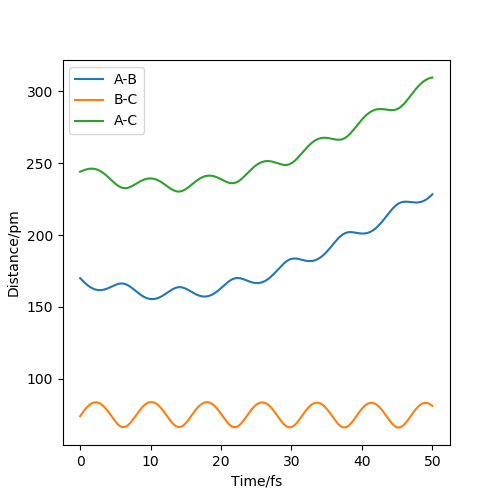

To make a reactive trajectory, the initial conditions were set as rHH=74pm and rHF=170pm for the F+H2 reaction. As an exothermic reaction, the energy was released for forming H-F. For figure 1, the momenta was set to: pHF=-0.1g.mol-1.pm.fs-1 and pHH=3g.mol-1.pm.fs-1 showing that the HF is not formed so not so much potential energy is transferred to kinetic energy to overcome the activation energy. For figure 2, the reactant has enough energy to overcome the activation energy thus HF is formed, the momenta was set to: pHF=-0.1g.mol-1.pm.fs-1 and pHH=20g.mol-1.pm.fs-1. Greater amount of kinetic energy has been transferred from potential energy, around +398 KJ mol-1.
Therefore, we can conclude that energy is released with the formation of HF bond where potential energy has been transferred to kinetic energy. The mean kinetic energy is related to its temperature, thus the increase in kinetic energy can be visualized by the heat released(temperature rise). We can use IR-Spectrometry to investigate the reaction and the heat release since the energy can be in the form of vibrational energy, and molecules will be in an excited state when H-F bond is formed.
ok Fdp18 (talk) 08:51, 27 May 2020 (BST)
Question 10
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
answer
Based on Polanyi's rules, we know that the energy requirement for a reaction to occur depends on the activation barrier location (transition state location). The translational energy is more effective than vibrational energy when the transition state resembles reactant more, while the vibrational energy is more effective if a transition state is closer to the product. The products of exothermic reactions normally have more vibrational energy than translational energy and characterized by early TS, the products should have more translational energy as it is more effective than having a lot of vibrational energy to overcome the energy barrier. Vice versa for endothermic reactions.
Two examples below support Polanyi's rules:

F + H2
rAB=225pm, rBC=74pm, pHF=-0.1g.mol-1.pm.fs-1 and pHH=6.1g.mol-1.pm.fs-1
This is an unreactive trajectory as the trajectory cannot pass the transition state and returns to its initial state. Reactants have relatively high vibrational energy with high amplitude but low translational energy.
This is not a good example, as the trajectory has not yet reached the interesting region. It might or might not react - you simply can't tell that yet. Fdp18 (talk) 08:54, 27 May 2020 (BST)

H + HF
rAB=225pm, rBC=90pm, pHF=20g.mol-1.pm.fs-1 and pHH=-0.5g.mol-1.pm.fs-1
This is a reactive trajectory since it passes the transition state without returning to the starting material. The large amplitude indicates that the reactants' vibrational energy is large. Trajectory passes through the transition state. While the amplitude of vibration decreases as the trajectory reaches the product region.
Unfortunately, this is also not a good example - the trajectory ends in the reactant's region. I would expect the reactants to be formed fully again, although you have not simulated for long enough to make that statement definitively. Fdp18 (talk) 08:56, 27 May 2020 (BST)
Reference
- Huheey, pps. A-21 to A-34; T.L. Cottrell, "The Strengths of Chemical Bonds," 2nd ed., Butterworths, London, 1958
- IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "transition state theory". doi:10.1351/goldbook.T06470
- Carey FA, Sundberg R (2007). Advanced Organic Chemistry Part A:Structure and Mechanisms. Norwell: Springer.
