MRD:01503585 yulong
EXERCISE 1: H + H2 system
Question 1: On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
The transition state is a saddle point on a potential energy diagram, it is a critical point but is not the local extremum Please give references (This one seems to be from Wikipedia). Fdp18 (talk) 15:45, 24 May 2020 (BST)
of the function. It can be identified by finding a point which its first and second derivative are both zero This is not entirely correct, at least not in more than one dimension. A rigorous mathematical way uses the definiteness of the Hessian. Fdp18 (talk) 15:50, 24 May 2020 (BST)
. The difference between the local minimum and transition state is that the local minimum has a non zero second derivative (positive derivative).
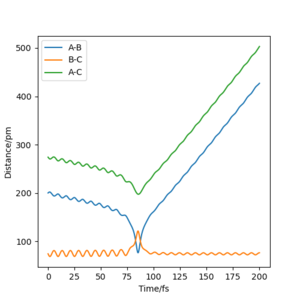
Question 2: Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
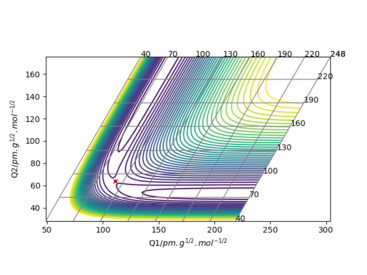
The estimate of mine is that the distance between AB and BC are both 90.78 pm. Based on the definition of the transition state, at the transition state, the atoms should have a fixed position. Based on the “Internuclear Distances vs Time”, the distances between atoms do not change with time, which means it is a good estimate of the transition state.
This is the correct value. However, I cannot see how you arrive there. You demonstrate that the value you present is the correct one, but you don't explain how you arrived there. This is important also for other reports - you need to show us what you did, otherwise the markers cannot distinguish whether you did the experiment yourself or just copied the results from someone else. Fdp18 (talk) 15:52, 24 May 2020 (BST)
Question 3: Comment on how the mep and the trajectory you just calculated differ.
The mep just include the minimum energy of the reaction passed, and it doesn't calculate the vibration of atoms while them moving, which its trajectory changes smoothly without fluctuation.
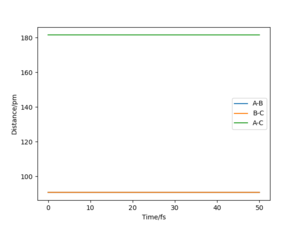
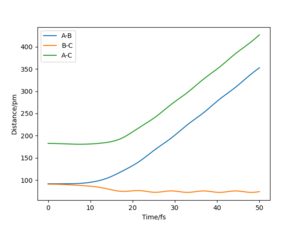
By comparing the "internuclear distances vs time" plots of r1=r2=rts and r1=rts, r2=rts+1, it is easy to obtain that when r1=r2=rts, the distances between atoms do not change. But as we change the starting point to r2=rts+1, the distance of between atoms A and C, and the distance between atoms A and B start to increase with a similar rate. While the distance between B and C starts to decrease. This difference between the two graphs shows that once the reaction passes the transition state, new molecule BC starts to form and at the same time atom A goes away from the molecule.


By comparing the "momenta vs time" plots of r1=r2=rts and r1=rts, r2=rts+1, we see that the momentum of B-C is fluctuating between 0.0024 g.mol-1.pm.fs-1 and -0.0024 g.mol-1.pm.fs-1. However, the real momenta of B-C and AB should both be zero at the transition state. The none zero values are caused by approximated input. For r1=rts, r2=rts+1, the momenta of A-B and B-C are both increasing. The momentum of A-B increases faster as A is going away from molecule BC, and reach a plateau. While the momentum B-C starts to fluctuate after increasing since they reach a vibrating status after forming a molecule.
For this and all Future reports: Please get in the habit of labelling your Figures+Tables+Equations+Schemes+..., and then referencing all of them in the text. Is is difficult for me to see which Figure belongs to what part of the text, and also what is a MEP and what is a dynamics trajectory. Fdp18 (talk) 15:58, 24 May 2020 (BST)
Question 4: Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?
| p1/ g.mol-1.pm.fs-1 | p2/ g.mol-1.pm.fs-1 | Etot | Reactive? | Description of the dynamics | Illustration of the trajectory |
|---|---|---|---|---|---|
| -2.56 | -5.1 | -414.280 | Reactive | At the start the distance between A and B is large and the distance between B and C is small since BC is a molecule. The momenta given are enough to let the reaction happen. When A collide molecule BC, new molecule AB is formed and molecule BC is broke. The kinetic energy for the reaction is 19.508 kJ.mol-1. How do you define the "kinetic energy for the reaction"? How do you calculate it? Fdp18 (talk) 16:03, 24 May 2020 (BST) |  |
| -3.1 | -4.1 | -420.077 | Unreactive | The distances between atoms at the starting point are similar to group one, but the molecule atoms have a larger momentum which causes the molecule has a greater vibration mode. The result of this is that the system has lower kinetic energy to complete the reaction. The kinetic energy for the reaction is 13.710 kJ.mol-1. |  |
| -3.1 | -5.1 | -413.977 | Reactive | The momentum of the molecule is the same as group 2, but the atom A has a greater momentum which causes the reaction has enough kinetic energy to complete. The kinetic energy for the reaction is 19.801 kJ.mol-1. |  |
| -5.1 | -10.1 | -357.277 | Unreactive | Under this condition, the momenta of both molecule and atom are so high which causes the bond between B-C breaks and A-B bond forms. However the reaction does not stop here, the bond between A-B breaks again and B-C bond forms again, which cause this reaction not completed. The kinetic energy for the reaction is 76.510 kJ.mol-1. |  |
| -5.1 | -10.6 | -349.477 | Reactive | For this one, the starting momenta are similar to group 4. However, the small excess of the momentum of atom A causes the system has enough kinetic energy to break the B-C bond again and finally form the A-B bond and leads the reaction to completion. The kinetic energy for the reaction is 84.310 kJ.mol-1. |  |
The hypothesis is "All trajectories starting with the same positions but with higher values of momenta (higher kinetic energy) would be reactive, as they have enough kinetic energy to overcome the activation barrier". Based on the result collected, this hypothesis is only partially correct. For some combination of starting momenta, the kinetic energy is too high to let the product stay stable. The extra kinetic energy will cause the reaction to fall back to reactants.
Question 5: Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
Based on the result obtained, the transition state theory predictions for rate values are overestimated.
According to the TST, systems with great enough energy will let the reaction happen. However, when the system with very high energy, the high energy vibration mode of it will cause the reaction goes to an unexpected result. Like the energy combination group 4 in question 4, the bonds between atoms form and break more than we need. Under this situation, some of the reaction predicted happen will not happen, which cause the predicted reaction rates higher than the real ones.
Besides, TST only involves classical mechanics but not quantum mechanics, which does not concern the effect of the "quantum tunnelling effect". This effect causes some reaction happens even it does not reach the activation energy. In this way, if the quantum tunnelling effect is concerned, the actual reaction rates will slightly higher than the ones predicted. However, this effect is minor which the overall TST predictions for rate values are still overestimated.
Sensible reasoning. However, and this is a general comment that applies for the whole report, many of your sentences are difficult to read/understand. I recommend to give your report(s) to someone else to read, maybe a family member or another student. It is difficult to find mistakes in the work you just wrote, even if you read it again. Fdp18 (talk) 16:08, 24 May 2020 (BST)
EXERCISE 2: F - H - H system
Question 6: By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
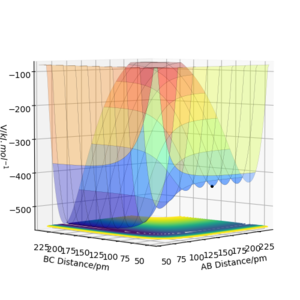
For this part, atom A now is Fluorine, and atoms B and C are hydrogens.
Where did you take the bond energies from? No references given! Fdp18 (talk) 16:10, 24 May 2020 (BST)
The bond energy of the H-F bond is 565 kJ/mol, and the bond energy of the H-H bond is 432 kJ/mol. The HF molecule has higher bond energy, which means more energy is needed to break the bond of HF than the bond of H-H. In this way, the reaction of F + H2 is an exothermic reaction and the reaction of H + HF is an endothermic reaction. The reason why HF has stronger bond energy is that HF molecule is polar and it has partial ionic character Yes, but not the only reason - Think about N2. It is not polar at all (It can't be because of symmetry), but nevertheless it is a very stable molecule...Fdp18 (talk) 16:11, 24 May 2020 (BST)
.
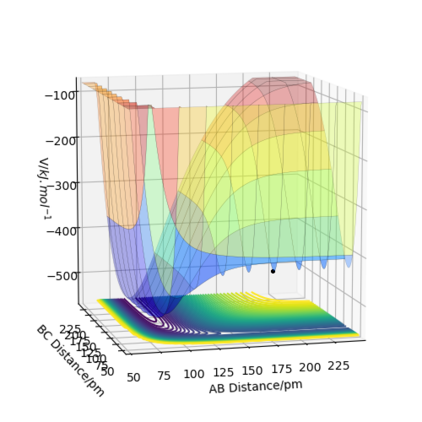
Question 7: Locate the approximate position of the transition state.
 |
 |
The approximate position of the transition state of this reaction is the point at rBC=74.49 pm and rAB=181.1 pm. Start simulation from this point, the distances between atoms remain unchanged. In this way, this is a good approximation of transition state point.
The same applies as for the transition state for the H-H-H reaction - I cannot see that you did the task yourself. Fdp18 (talk) 16:13, 24 May 2020 (BST)
Question 8: Report the activation energy for both reactions.kJ/mol
Set the calculation type as MEP, by changing the atom distances, we can obtain the activation energy for two reactions. At the transition point, the total energy of the system is -433.981 kJ/mol.
For F + H2, set the distance between atom F and H2 rAB=1000pm, and keep rBC=74.49 pm:
The energy obtained when time is long enough is -435.059 kJ/mol, and the activation energy for this reaction thus is -433.981 kJ/mol-(-435.059 kJ/mol)=1.078 kJ/mol.
For H + HF, set the distance between atom H and HF rBC=1000pm, and keep rAB=181.1 pm:
The energy obtained when time is long enough is -560.7 kJ/mol, and the activation energy for this reaction thus is -433.981 kJ/mol-(-560.7 kJ/mol)=126.719 kJ/mol
This part looks like you really understood what you're doing, and I like it. However, what I assume is that you did a MEP run after setting the distances you give above, and then taking the energy of the relaxed structure. This is not mentioned explicitly - please make sure to include such little procedural details in the future. We want to reward you for what you did, but you need to show it to us first. Fdp18 (talk) 16:15, 24 May 2020 (BST)
Question 9: In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.
For reaction F + H2
The distances set are rHH = 74 pm, rFH=200 pm.
For diagram 1, the kinetic energy is quite high at the beginning. After the H2 molecule and Fluorine atom react, the bond between H and F forms and breaks several times. The kinetic energy and potential energy converse to each other several times. In the end, since the kinetic energy is too high, the high vibration mode causes the bond of HF breaks and then the reaction is unreactive.
For diagram 2, the kinetic energy is enough to let the reaction happen and not break the HF bond forms in the end. Some kinetic energy stores in HF bond and some potential energy stored in HH bond turns into kinetic energy.
Diagram 3 is similar to diagram 2, and diagrams 4 & 5 is similar to diagram 1.
For the combination of pFH= -1.6 g.mol-1.pm.fs-1 and pHH= 0.2 g.mol-1.pm.fs-1, the reaction is unreactive since the momentum of the system is too low to overcome the barrier of the reaction. Thus the reaction does not happen.
For reaction H + HF

For the reaction of H + HF, one possible initial condition found is rAB = 92 pm, rBC = 200 pm, and the momenta are pFH= 0 g.mol-1.pm.fs-1 and pHH= 0.2 g.mol-1.pm.fs-1. The energy of the system is -270.348 kJ/mol. This reaction can happen is because the H atom has enough energy to break the HF bond and form a new HH bond. Since the bond energy of HF is very high, the H atom needs more momentum to start the reaction.
To confirm the observations experimentally, controlling temperature of the reaction is a good way. By increasing the temperature, the momenta of molecules and atoms increases. So the reaction starts to change from unreactive to reactive. However, if the temperature is too high, which causes extra momenta in the reaction, the high energy vibration mode will cause the product to fall back to the reactant.
Here I can see what you did. You looked very thoroughly at the two systems. However, you'll want to look at the conclusions you draw again - you mixed up thermodynamics and kinetics. Fdp18 (talk) 16:19, 24 May 2020 (BST)
Question 10: Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
Based on Polanyi's empirical rules, the vibrational energy more likely to promote the late-barrier reaction and the translational energy more likely to promote the early-barrier reaction. Please provide references! Fdp18 (talk) 16:19, 24 May 2020 (BST)
For the reaction of F + H2, it is an exothermic reaction with an early transition state, which is an early-barrier reaction. In this way, it is more likely to be promoted by translational energy. Thus when pHF (leads to translational energy)is relatively larger, the reaction is more likely to happen.
For the reaction of H + HF, it is an endothermic reaction with a late transition state, which is a late-barrier reaction. In this way, it is more likely to be promoted by vibrational energy. Thus when pHF (leads to vibrational energy) is relatively larger, the reaction is more likely to happen.
It would be good if you could back up such statements with simulation results. For example, exemplary reactive and unreactive trajectories as a result from different choices of pHF.Fdp18 (talk) 16:23, 24 May 2020 (BST)