MRD:01502946

4/5 - A generally good first section. You provided clear and well reasonsed responses to the questions. Your second section was also generally good but had 1 or 2 areas of misunderstanding that you should try to address.

Exercise 1

Question 1) Definition of the TS

On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?

The transition state is defined as the maximum located on a minimum energy path. Mathematically, it is a saddle point on the potential energy surface. At TS coordinates, 𝛿V(x,y)/𝛿x = 0 and 𝛿V(x,y)/𝛿y = 0, where x and y are r₁ and r₂ in this case. Additionally at TS coordinates, the second partial derivative with respect to one of the coordinates is positive and negative with respect to the other coordinate, i.e either 𝛿²V(x,y)/𝛿²x > 0 and 𝛿²V(x,y)/𝛿²y < 0 or 𝛿²V(x,y)/𝛿²x < 0 and 𝛿²V(x,y)/𝛿²y > 0. This fact allows the saddle point to be simply distinguished from a local minimum as at the latter, both 𝛿²V(x,y)/𝛿²x > 0 and 𝛿²V(x,y)/𝛿²y > 0.

A solid definition of the TS and saddle point, well done.

Question 2) H + H₂ TS position

Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

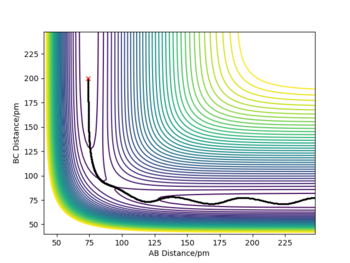
If r₁ = r₂ = r_ts and p₁ = p₂ = 0, the atoms are expected to stay still and not oscillate as the attractive and repulsive forces are perfectly balanced. Therefore, E_kin of the atoms will be 0, given such initial conditions and E_pot = const., as illustrated by the figure below. The TS coordinates can also be estimated by the surface plot and the reaction trajectory, which at mentioned initial conditions will converge into a single spot on the E_pot surface, which is the transition state. Using this method, r_ts was estimated to be equal to approximately 90.77 pm for the H + H₂ system.

Sensible estimate for the TS, and well reasoned. Well done!

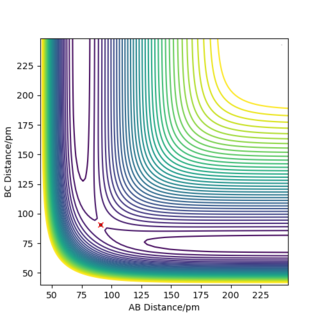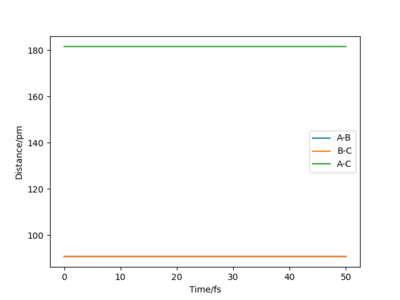Question 3) MEP&dynamic trajectories

Comment on how the mep and the trajectory you just calculated differ.

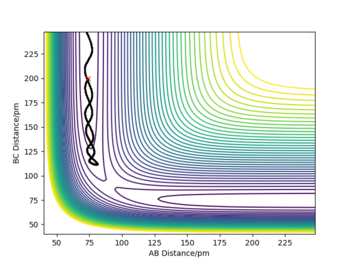
For the MEP path, no vibrational motion of the formed H₂ is observed unlike in the case of dynamic mode. Over the course of the reaction, some of the initial potential energy is changed into kinetic energy. When molecular hydrogen forms, some of the kinetic energy is converted into vibrational energy, which is indicated by the oscillations on the PE surface. In the case of MEP, the reaction proceeds via a pathway with smallest possible total energy. In order to minimise the total energy, vibrational energy must be minimised as well. Consequently, no vibrational motion is observed in the MEP mode. As the MEP mode corresponds to infinitely slow motion of the nuclei, no changes in momenta or velocities are observed either. Furthermore, total energy of the system is not conserved in the MEP mode. The total potential energy of products is lower than the potential energy at TS but as the system has no kinetic energy at any point, E_pot must be equal to E_tot. This seemingly violates the law of conservation of energy, but that it is just the result of assumptions made in the MEP mode. On the other hand, energy is conserved in the dynamics mode as motion of the atoms is not taken to be infinitely slow.

good explanation!

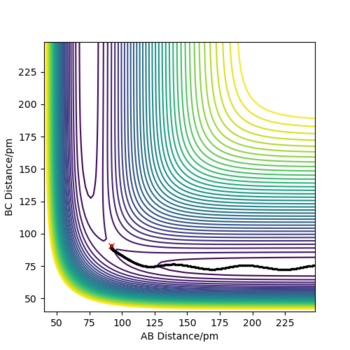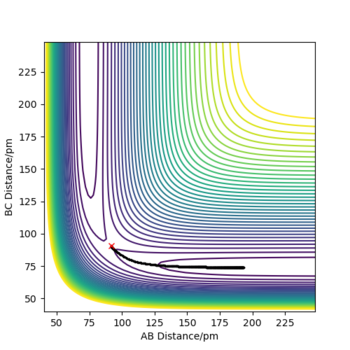Look at the “Internuclear Distances vs Time” and “Momenta vs Time”. What would change if we used the initial conditions r₁ = r_ts and r₂ = r_ts+1 pm instead?

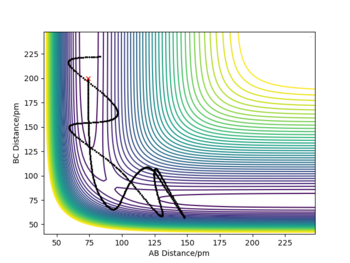
All three atoms are the same elements and only the definitions of r₁ and r₂ are interchanged, therefore the outcome of the reaction will still be chemically the same. The only difference is that the chemical bond will be formed between the hydrogen in the middle and the proton that previously ended up as a free radical (instead of H_A + H_B + H_C --> H_A + H_B-H_C, we get H_A-H_B + H_C). On Internuclear Dist. vs Time and Momenta vs Time plots, the lines which previously represented parameters associated with r_A-B now represent r_B-C and vice versa (see figures below).

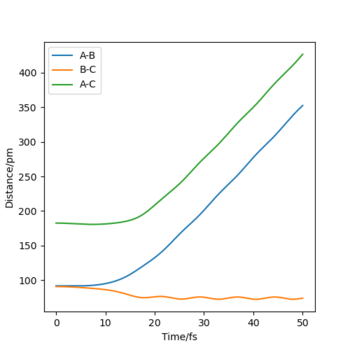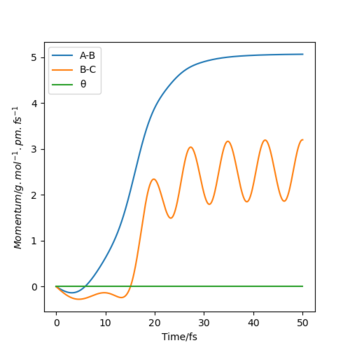Take note of the final values of the positions r₁(t) r₂(t) and p₁(t) p₂(t) for your trajectory for large enough t. Setup a calculation where the initial positions correspond to the final positions of the trajectory you calculated above, the same final momenta values but with their signs reversed. What do you observe?

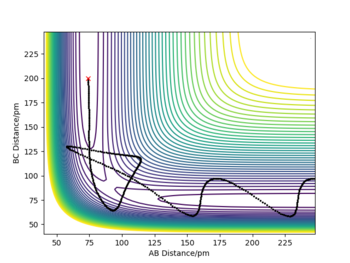
The atoms return from the products to the transition state and stay there as the TS structure described in question 2. Essentially, it is the reverse process of TS structure converting into products.

Question 4) A nice table (I agree, it is a very nice table)

Complete the table below by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory.

Note: In this case, r₁ and r₂ correspond to r_A-B and r_B-C, respectively. The units for p are g·mol^-1·pm·fs^-1.

p₁	p₂	E_tot (kJ/mol)	Reactive?	Description of the dynamics
-2.56	-5.1	-414.27	Yes	H_A-H_B has very little vibrational energy. Collision with H_C occurs with sufficient energy to convert H_A-H_B into H_B-H_C, which oscillates slightly as the distance between H_A and the newly formed H₂ increases.
-3.1	-4.1	-420.08	No	The collision of H_C of H_A-H_B is not energetic enough to form H_B-H_C. The energy barrier is not crossed and the H₂ molecule continues oscillating as H_C recedes.
-3.1	-5.1	-413.98	Yes	H_A-H_B has some vibrational energy. The collision occurs with sufficient energy and H_A-H_B is converted into H_B-H_C. The newly formed dihydrogen oscillates more heavily than the initial molecule. The reaction proceeds via a slightly higher energy pathway than in the first case as the vibrational energy of the starting material is greater.
-5.1	-10.1	-357.27	No	H_C collides with H_A-B with sufficient energy to form H_B-Cbut as a result of the product having high vibrational energy, the starting materials are reformed. The vibrational energy is illustrated by the high energy oscillations seen in the figure on the right.
-5.1	-10.6	-349.48	Yes	H_C collides with H_A-H_B once again with sufficient energy to form H_B-H_C, but as r₁ is small enough and H_B-H_C undergoes high energy oscillations, H_A-H_B is reformed. However, in this case H_C experiences a high attractive force to H_A-H_B and stays relatively close to the molecule. Upon stretching of the H_A-H_B bond, H_B-H_Cis reformed and H_A departs as a single atom. H_B-H_C oscillates heavily, but attractive forces to H_A decrease continuously due to increasing r₁.

What can you conclude from the table?

The reactants must be sufficiently high in energy for the reaction to occur, but their energy must be also be suitably distributed between translational and vibrational forms. Otherwise, the reaction can possibly revert back to starting materials even after crossing the TS due to high energy oscillations brought about by the collision, as illustrated by the different initial conditions listed in the table above.Good conclusion.

Question 5) Transition state theory

Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

The differences between TST predictions and experimental rate constant values are the direct result of assumptions made in calculations based on TST.¹

The motion of nuclei is described only by classical mechanics and any quantum effects are neglected. This has a great influence on simple reactions involving light particles (H, D), as possible quantum tunneling is not taken into account. In reality, light particles can tunnel through narrow low energy barriers and this is especially likely in given simple case. Therefore in the case of reaction H + H₂, employing TST will result in underestimation of the rate constant. Nevertheless, other influences of TST assumptions should be considered in conjunction with this one and therefore the rate constant might still be overestimated, regardless of quantum mechanical effects. In reactions involving more massive atoms or higher energy barriers, neglecting quantum behaviour of particles and tunneling will likely have no effect on the predicted rate constant as the probability of tunneling decreases exponentially with increasing particle mass. Good! Keep in mind that even for hydrogen and deuterium, tunneling is still a weak effect. This is why-- among other things-- processes like nuclear fusion are so difficult.
Every collision with sufficient kinetic energy will definitely cross the TS and will go on to form the products. Furthermore, conversion to products is considered to be irreversible: reactants that have reached the transition state will not revert back to starting materials. In reality, the TS can revert back to starting materials as well. As illustrated by the entries in the table above, products are often able to recross the TS and convert back into starting materials, given a suitable distribution of translational and vibrational energies. Additionally, reactions leading back to starting materials can still occur, although this will have a small effect if the forward equilibrium constant is very large. As a consequence, these assumptions of TST would overestimate the rate constant for reforming starting materials decrease the total reaction rate. Good!
The transition state structure is in quasi-equilibrium with the reactants and the particles follow a Boltzmann distribution of energies. In addition, TS structures are sufficiently long-lived to reach a Boltzmann distribution of energies as well before converting to products. Although the thermal equilibrium is not very important in H + H₂ system, in very fast reactions the nuclei might not reach a Boltzmann distribution of energies before colliding. Furthermore at very high temperatures, higher energy levels are populated, thus breaking the assumption that only low vibrational states are populated. If the average energies of particles are different from what is predicted, the fraction of sufficiently energetic collisions leading to TS cannot be accurately estimated either. This could result in poor estimates for the rate constant as crossing the energy barrier to form TS is rate limiting.

Good explanation of the deficiencies of TST. On balance, taking all of the above into consideration, will TST overestimate or underestimate?

Exercise 2

Question 1) Energetics of F + H₂ and H + HF

By inspecting the potential energy surfaces, classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

The reaction between F + H₂ is exothermic, as the energy of the products (HF + H) is lower than that of the reactants. Conversely, the reaction H + HF is endothermic, as the products are higher in energy than the reactants. The bond energies of H-F and H-H bonds are 565 kJ/mol and 436 kJ/mol, respectively.² As the H-F bond is stronger than the H-H bond, energy is released as heat upon formation of HF from F and H₂. In the reverse reaction, more energy is needed to put into breaking of the H-F bond, which results in the reaction being endothermic.

Question 2) F + H₂ TS position

Locate the approximate position of the transition state.

In this case, A = F, B = C = H and therefore, r₁ = r_A-B and r₂ = r_B-C

At the transition states, all repulsive and attractive forces are balanced. Consequently, E_tot = E_pot = const.

Such conditions are satisfied at: r₁ = 181 pm and r₂ = 74.5 pm, given p₁ = p₂ = 0 g·mol^-1·pm·fs^-1. This result was obtained through trial and error, but the TS could also be located through decreasing the spacing between isoenergetic contour lines and searching for the saddle point (although in this case even the smallest spacing does not give a very precise answer). The equilibrium bond lengths of H₂ and HF are r_H2 = 74 pm and r_HF = 91.7 pm, respectively.² The large difference between r₁ and r_HF and small difference between r₂ and r_H2 indicates an early transition state as the TS structure is highly similar to the starting materials. The reaction is exothermic and an early TS is also predicted by the Hammond postulate: the TS structure (and its energy) must be similar to starting materials (and their energy) as the reaction cannot proceed before the energy barrier leading to the TS has been crossed.

Sensible answer, well done.

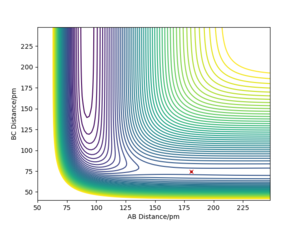
Question 3) Activation energies

Report the activation energy for both reactions.

Reaction: F + H₂ (E_a = 0.995 kJ/mol)

Reaction: H + HF (E_a = 126.57 kJ/mol)

Sensible estimates for Ea in both directions. I'd say that your Ea for F+H2 is ever so slightly too low, but only a little.

The activation energies were determined with the help of energy vs time plots by the following procedure.

Firstly, the total energy at an arbitrarily chosen position (r₁ = 74 pm, r₂ = 300 pm) on the "starting materials valley" floor was determined. This corresponded to the total energy of starting materials before the reaction (E_SM). The r values correspond to a H₂ molecule at equilibrium bond length and a fluorine atom far away from H₂. Note that p₁ = p₂ = 0 (same in further steps) and that using a larger r₂ value can give a slightly smaller total energy value, but this is a sufficient approximation.
Secondly, the total energy at TS (E_TS) was determined (see the previous question).
Finally the total energy at an arbitrarily chosen position (r₁ = 300 pm, r₂ = 91.7 pm) on the "products valley" floor was determined. This corresponded to the total energy of products after the reaction (E_PR). The r values correspond to a HF molecule at equilibrium bond length and an hydrogen atom far away from HF.

The difference between E_TS and E_SM was then calculated to yield the activation energy of reaction F + H₂. The activation energy of the reverse reaction was found similarly for E_TS and E_PR.

Question 4) A reactive F + H₂ trajectory

Identify a set of initial conditions that results in a reactive trajectory for the F + H₂, and look at the “Animation” and “Momenta vs Time”. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.

Similarly to 2), A = F, B = C = H and therefore r₁ = r_A-B and r₂ = r_B-C. The figure below illustrates the outcome of reaction F + H₂ at the following initial conditions:

r₁ = 180 pm, p₁ = -1.4 g·mol^-1·pm·fs^-1;

r₂ = 74 pm, p₂ = -0.4 g·mol^-1·pm·fs^-1.

NB: the step number must be set higher than 500 at size 0.1 fs to see the outcome.

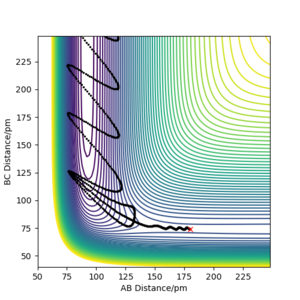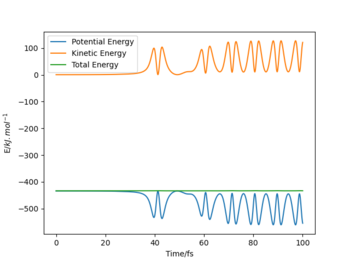As the initial momenta are relatively small, the potential energy is approximately equal to the total energy. Initially, there is a small component of kinetic energy, but as the initial momenta are small, its contribution is negligible. As H₂ approaches F, the kinetic energy component increases quickly. When HF is formed and atomic hydrogen departs, a portion of the potential energy is converted into vibrational energy. The potential and kinetic energy components change accordingly as the formed diatomic molecule oscillates. The H-F oscillations are considerably stronger than the initial H-H oscillations. Note that the potential energy does not reach the total energy value as the atomic hydrogen will have kinetic energy as well. As the single proton cannot undergo vibrational motion on its own and no force acts upon it (due to increasing r₂ value), it will move with constant velocity and therefore constant kinetic energy.

Experimentally, the reaction could be confirmed by femtosecond absorption spectroscopy, in which molecules are excited electronically by a short laser pulse (lasting ca 1 ps) to a dissociative state. After a short interval, the excited molecule is exposed to another pulse at the absorption wavelength of one of the products. From the presence of dissociation product absorption bands and their relative intensities with respect to the excited molecule absorption bands (HF in this case), composition of gas-phase reaction mixtures can be probed.³In addition, vibrational or rotational spectroscopy could be used too as H₂ and HF give distinct bands in the spectra. This is due to the excitation frequencies of H₂ being higher than those of HF as fluorine is ca 19x more massive than hydrogen. It is known from spectroscopy that v_vib ∝ √(k/μ) and v_rot ∝ 1/μ, where v_vib and v_rot are vibrational and rotational frequencies (Hz), respectively, k is the bond force constant and μ is the reduced mass of the diatomic species. As μ(H₂)<μ(HF), both the values of v_viband v_rot are expected to be greater for H₂. Although k(H₂)<k(HF), the difference in reduced masses outweighs the difference in force constants and v_vib will nevertheless be greater for H₂. Remember that H2 is symmetric though and therefore the transition is likely to be IR inactive. If you were to run this reaction, any IR signatures would be from HF. I think you're a bit confused here about what you're looking for. fs-TA would not really be suitable for this experiment as you've described it (as a photodissociation followed by a probe). Your vibrational spectroscopy idea is better but you've not explained how this could be used to monitor energy release. Think about what happens if a molecule is vibrationally excited and what changes to the IR spectrum would occur.

NB: The relationship v_rot ∝ 1/μ assumes a rigid rotor model, but experimentally any centrifugal distortions must be taken into account.

Setup a calculation starting on the side of the reactants of F + H₂, at the bottom of the well r_HH = 74 pm, with a momentum p_FH = -1.0 g.mol^-1.pm.fs^-1, and explore several values of p_HH in the range -6.1 to 6.1 g.mol^-1.pm.fs^-1 (explore values also close to these limits). What do you observe? Note that we are putting a significant amount of energy (much more than the activation energy) into the system on the H - H vibration.

Conversion to products seems to be more likely at low p values (in the range -2 to 2 g.mol^-1.pm.fs^-1). Although conversion is likely at values around -6.1 and 6.1 g.mol^-1.pm.fs^-1 as well, small changes in p value seem to have a great influence on the outcome of the reaction. On the other hand, at small initial momenta values, small changes (+-0.05 g.mol^-1.pm.fs^-1) seem to have little effect on the outcome.

For the same initial position, increase slightly the momentum p_FH = -1.6 g.mol^-1.pm.fs^-1, and considerably reduce the overall energy of the system by reducing the momentum p_HH = 0.2 g.mol^-1.pm.fs^-1. What do you observe now?

The products are formed. Increasing p_HH has little effect on the outcome until values of ca 2 - 1.6 g.mol^-1.pm.fs^-1.

Question 5) Distribution of energy

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

In endothermic reactions, the TS occurs early in the reactant channel. This means that the TS structure of the starting materials best resembles the TS structure. On the other hand, in exothermic reactions, the TS occurs late in the products channel. This means that the TS structure of the products is more close to the TS structure. According to Polyani's empirical rules, the translational component of reactant energy is more important in crossing an early TS and vibrational energy is more important in overcoming a late TS.⁴

As illustrated by the exothermic reaction between F and H₂, products are unlikely to form if the vibrational component of H₂ is high and translational component is low. If H₂ is just busy oscillating and the colliding species do not have sufficient kinetic energy, the early TS is unlikely to be crossed and the H-H bond is not broken. Although formation of the stronger H-F bond is energetically favoured, it cannot happen if the collision itself is not energetic enough.

Conversely, in the endothermic reaction between H and HF, the vibrational energy of HF has a key role in the success of the reaction. Even if the kinetic energy of H is high but the vibrational energy of HF is low, products are again unlikely to be formed. In order to cross the late TS, the strong HF bond has to have sufficient vibrational energy in order to be broken upon collision with the free H. As shown previously, the fluorine atom attracts the leaving hydrogen quite strongly so unless the HF bond oscillates heavily before the collision, H₂ cannot form as the strong attractive forces of fluorine cannot be overcome even when collisions occur with high kinetic energies.

As a result, reactions might not proceed even if the system has enough energy to overcome the TS barrier or to irreversibly convert to the products having crossed the TS. The key to successful reactions lies among other factors in the distribution of energy between different modes of molecular motion.

Good answer. I'd have liked to have seen an example for the late TS case though.

References

1. Steinfeld J. I., Francisco J. S., Hase W. L. Chemical Kinetics and Dynamics 2nd Edition, pg 315-318. Prentice-Hall.

2. Atkins P., de Paula J. (2014) Physical Chemistry 10th Edition, pg 985. Oxford University Press.

3. Atkins P., de Paula J. (2014) Physical Chemistry 10th Edition, pg 898. Oxford University Press.

4. Steinfeld J. I., Francisco J. S., Hase W. L. Chemical Kinetics and Dynamics 2nd Edition, pg 272-274. Prentice-Hall.