MRD:01499685

EXERCISE 1: H + H₂ system

Q1. On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?

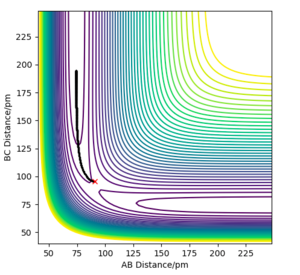
Potential energy surface showing the minimal energy path, and the dividing surface through the transition state is at right angles to the minimum-energy path, as it is the alternative dividing surface. A saddle point is produced on the graph. The transition state is the maximum in energy (saddle point) along the reaction pathway. On the potential energy surface diagram, the saddle point is minimum when viewing potential against r1/r2. However, it is maximum for the angle orthogonal to it. Furthermore, local minimum of the potential energy surface usually represents products or intermediates. Mathematically, the transition state can be defined using first and second derivatives. The first derivative equals to zero, and the second derivative should be a negative value. Second derivatives can be used to distinguish the saddle point or the local minimum of the potential energy surface. Do you mean r1+r2 rather than r1/r2? This whole section is difficult to understand. If you have the time, I would recommend you for future reports to wait a bit and then read it again. Or even better, give it to someone else to read, if they don't understand it you need to rephrase. Fdp18 (talk) 13:15, 16 May 2020 (BST)

The 2nd derivatives can also be used to distinguish maxima from saddle points and minima. How does that work? Think about the signs of the 2nd derivatives in *all* your dimensions! Fdp18 (talk) 13:16, 16 May 2020 (BST)

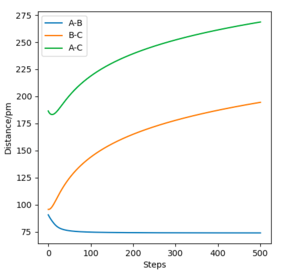
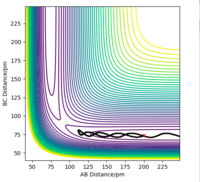
Q2. Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

If the system starts at the transition state with no momentum, there will be no force acting on the atom, so the atom will not oscillate. In the H-H-H system, the transition state should be symmetrical, so AB=BC, and no force acts on AB or BC. The best estimate of the transition state position is 90.775 pm. The internuclear distance vs time plot demonstrates that at this specific bond length, line AB overlaps line BC and remains constant.

This is a good, concise explanation. Fdp18 (talk) 13:17, 16 May 2020 (BST)

Internuclear Distances vs Time plot for transition state

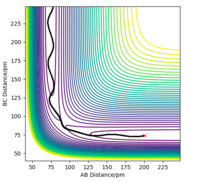
Q3. Comment on how the mep and the trajectory you just calculated differ.

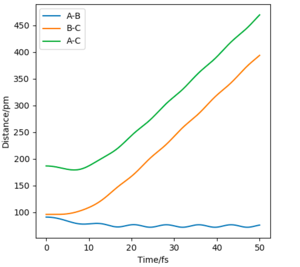
Under the same condition ( r₁ = r_ts+5 what is "5" here? 5 bohr? 5 Anströms? Please use units - if you don't, a reader might assume atomic units, which would be bohr here. And that's still ambigous because there are different sets of atomic units. Fdp18 (talk) 13:18, 16 May 2020 (BST) , r₂ = r_ts), the potential energy equals to the total energy. While on mep calculation, there is no change in momenta. However, the dynamics calculation includes the change in momentum. The momentum graphs illustrate that dynamic calculation involves the vibration motions of molecules.

r1 = rts+5, r2 = rts on mep calculation	r1 = rts+5, r2 = rts on dynamics calculation
intermolecular distance on mep calculation	momentum on mep calculation
intermolecular distance on dynamics calculation	momentum on dynamics calculation

Q4. Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?

p1/ g.mol-1.pm.fs-1	p2/ g.mol-1.pm.fs-1	Etot	Reactive?	Description of the dynamics	Illustration of the trajectory
-2.56	-5.1	-414.280	reactive	The H atom and H2 molecule approach to each other, and the system has enough energy to across the energy barrier then form the product.
-3.1	-4.1	-420.077	unreactive	The atom is approaching to the molecule, then they separate again since they don't have enough energy to overcome the activation energy.
-3.1	-5.1	-413.977	reactive	The atom is going to react with the molecule and the gives the product. It across the col to form product without bouncing back.
-5.1	-10.1	-357.277	unreactive	The reactants just collide with each other, they pass the transition state and then back to reform reactants.
-5.1	-10.6	-349.477	reactive	It is able to across the transition state, then encounter a potential energy wall and bounce back. After that, it across the transition state for the second time to form the product.

From the example above, it illustrates that sometimes even the system has enough energy to across the col, it is still possible to reform reactants. The transition state theory assumption is not valid for this situation. This reveals the transition state theory overestimate the experiment values (which will be interpreted below)

Q5.Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

Conventional Transition-State Theory has some assumptions:

1. Once the molecular systems surmounted the transition state, it is not able to turn back and form reactant again.

2. The energy distribution of the reactant is determined by Maxwell-Boltzmann distribution. Moreover, the con-concentration of those activated complexes that are becoming products can also be calculated using equilibrium theory.

3. The motion along the transition state can be separated from other motions associated with the activated complex.

4. The chemical reactions can be treated using classical motion and ignore quantum effects.

Stating the assumptions of what you are to comment on is a good approach, and you have also thought of giving references. Continue to do this in future reports, it is good practise. Fdp18 (talk) 13:22, 16 May 2020 (BST)

The Transition State Theory prediction underestimate the reaction rate values compare with experimental values. Because the transition state theory assumes that once the reactant across the energy barrier and it cannot back to reactant. However, in the actual experiment, the reactants can go across the transition state and form products, then reform the reactants. Besides, CTST calculation only use standard expressions. The vibrational expression is a quantum expression, but it assumes the vibrations are harmonic. However, this is not true at high temperature.Moreover, the transmission may lower than unity due to an alternative reaction path. Additionally, tunnelling is probable for a thin energy barrier. Also, tunnelling is most important for the transfer of particles of small mass, but this effect is negligible for heavier species.

EXERCISE 2: F - H - H system

This is a general remark for the whole second part: I don't have any indication that you did any of the simulations. To name an example, for Q5 you could have shown four trajectories showing the successful and unsuccesful pathways for early and late transition state. Fdp18 (talk) 13:33, 16 May 2020 (BST)

There is no plot of any kind in this section (distance, energy, momentum, trajectory on contour plot...). For the future: please show what you did. We can only grade you for what you hand in. Fdp18 (talk) 13:35, 16 May 2020 (BST)

Q1. By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

F+H2 reaction is an exothermic reaction. Since H can form a stronger bond with F, it will release more energy when forming the new H-F bond. It only needs a little energy to break the H-H bond to reach the transition state. Overall, it is an exothermic reaction. Nevertheless, H+HF reaction is a backward reaction. Therefore, this reaction has to be an endothermic reaction.

That is correct, but how did you arrive there? What is the bond strength? Fdp18 (talk) 13:23, 16 May 2020 (BST)

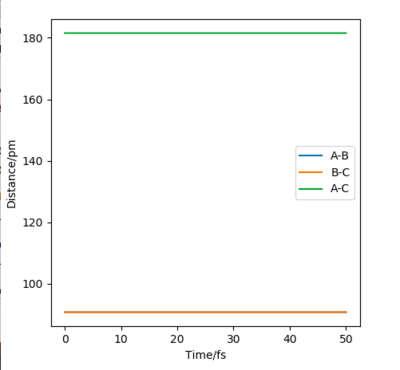
Q2. Locate the approximate position of the transition state.

Since this reaction of F + H2 is an exothermic reaction, the transition state has a energy closer to the reactant. Based on the Hammond's Postulate, the structure of the transition state will resemble the reactant. This type of transition state is defined as early transition state. In the F-H-H system, the H-H bond will not be elongated too much, so the bond length is 74.5 pm. Then set the momentum zero and test the different value of the distance between F and H, which gives the approximate position of the transition is around 181.8 pm.

very brief, but not wrong per se. Fdp18 (talk) 13:24, 16 May 2020 (BST)

Q3. Report the activation energy for both reactions.

Activation energy is the energy difference between transition state and reactants. By rolling down the molecule from the highest energy level with zero momentum, the energy level of reactant is able to be found. The total energy of the transition state is -433.981 kJ/mol. When the distance of AB increases to 600 pm, the total energy is -435.057 kJ/mol. The total energy keeps unchanged if the distance of AB keeps increase. Therefore, the activation energy for F+H2 reaction is 1.076 kJ/mol.

Please define all your quantities properly when you use them - in this case AB. Fdp18 (talk) 13:25, 16 May 2020 (BST)

Q4. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.

The types of released energy are electronic, vibrational, rotational, and translational energy. However, the excited electronic levels are too high for standard temperature. The partition function for translational motion in three degrees of freedom involves only the mass of the molecule. The rotational partition function for a linear molecule involves the moment of inertia I. In a non-linear molecule which contains N number of atoms, the three degrees of freedom relates to rotational energy, and 3N-6 relates to vibrational energy. This can be examined by IR spectrum.

Also very brief. You mention the components of the rigid rotor / harmonic oscillator / free particle approximation. However, you don't seem to use them, only the vibrational component. Thus, the only sentence related to this question is "This can be examined by IR spectrum", which is not enough. For future reports: try to be focused on what you want. It is ok if you decide that talking about rotation is important here, for example. However, then you should make a connection to the rest of your work. In this case you could e.g. talk about (angular) momentum and it's conservation. Fdp18 (talk) 13:29, 16 May 2020 (BST)

Q5. Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

For an exothermic reaction, the transition state resembles the reactant. This early transition state has more efficient translational energy because the motion corresponds to the separation of products. Besides, the late transition state appears in endothermic reaction, which makes vibrational energy more efficient.

This is not entirely correct. The first part of the argument can also be used for late transition states. Please look up Polanyi's rules. Fdp18 (talk) 13:31, 16 May 2020 (BST)