MRD:01496586
Overall good. I would definitley Mys18 (talk) 02:24, 23 May 2020 (BST)
This is a good report with understanding shown throughout. There are areas which could have been improved with further detail in your answers, see comments below. Additionally, it was difficult to study your figures, so perhaps as a rule of thumb, go back and check your submission is how you intended it to be.Mys18 (talk) 02:26, 23 May 2020 (BST)
Year 2 Molecular Reaction Dynamics Lab
== Exercise 1: H+H2 system
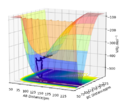
Q1: On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface? The plot below shows the potential surface diagram of an H and H2 collision where the transition state is H-H-H.
On a potential energy surface diagram, in between 2 minima a saddle point can be seen in which the lowest energy path passes through. This saddle point is known as the transition state. At T=0, all atoms will want to be in the lowest possible potential energy. The saddle point will have a negative slope on one side and a positive slope on the other therefore meaning that the slope of the function will be zero, where: Unlike the minima, at the saddle point once the second derivatives are calculated, one will be positive while the other negative so that:
At the transition state, the potential energy surface will have a higher energy than the reactants or products; this can be used to identify the transition state. Moreover, at the local minima both derivates will be positive due to the positive curvature, where:
This is correct, but could be phrased slightly more clearly. The maximum of the lowest-energy pathway is the TS represented as the saddle-point. Good, it is a minimum in one direction and a maximum in the other whereas a local minimum is a minimum throughout. Mys18 (talk) 01:48, 23 May 2020 (BST)
Q2: Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
It can be seen in the contour plot that there is a line of symmetry going through the origin and the cross of this plot showing that this H +H2 system is symmetric meaning that in the transition state r1=r2. Additionally, the transition state is a stationary point meaning that the momentum of both H and H2 is 0. Consquently, using the conservation of momentum, rts can be calculated as rts=90.8 (r1=r2=90.8).
This Internuclear Distance vs Time plot depicts how there is minimal to no oscillation at these values of r, which is in correlation of what should occur at the transition state. By altering the values of r, the oscillations would change, decreasing when nearing the value of rts.
Q3: Comment on how the mep and the trajectory you just calculated differ.
In the minimal energy path contour plot, the trajectory is simply a smooth line with no oscillations as the momenta are always set to zero. At any point on the path the energy is at a minimum.
In the dynamic contour plot, the calculation shows a slight oscillation due to the slight displacement from the transition state where r1=91.8 and r2=rts=90.8.
Your figures throughout are too small to interpret (at least from my side), consider resizing them before submission. What does the Dynamic calculation consider making it a more realistic model? Hmmm... those values could mean anything, remember always include units.Mys18 (talk) 01:58, 23 May 2020 (BST)
Q4: Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?
| p1/ g.mol-1.pm.fs-1 | p2/ g.mol-1.pm.fs-1 | Etot | Reactive? | Description of the dynamics | Illustration of the trajectory |
|---|---|---|---|---|---|
| -2.56 | -5.1 | -414.280 | Yes | reaction occurs where A + B-C -> A-B +C, before collision, the trajectory is smooth whereas after the collision there is some oscillation | |
| -3.1 | -4.1 | -420.077 | No | The reaction does not occur as the H atom bounces back, unable to break through the activation barrier at the saddle point | |
| -3.1 | -5.1 | -413.977 | Yes | reaction occurs where A + B-C -> A-B +C, however compared to the first reaction atom A has greater inital energy | |
| -5.1 | -10.1 | -331.777 | Yes | the inital reaction does occur where A + B-C -> A-B +C, however A recrosses the barrier to eventually form the final product A-B->C | |
| -5.1 | -10.6 | -326.477 | Yes | The trajectory of the reaction is almost identical to that of reaction 4 however with a slightly lower total energy |
The table above illustrates how barrier recrossing can occur, where the potential barrier separating the two species is crossed followed by return to the initial form.
Good, what about the relevance of having enough energy to overcome the transition barrier. Even if this is overcome is the trajectory always reactive? You have answered this, but a more detailed observation would be preferred. Mys18 (talk) 02:03, 23 May 2020 (BST)
Q5: Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
The Transition State Theory assumes that intermediates have a lifetime long enough for its states to be portrated in a Boltzmann distribution; however, in reality this is not the case as in most reactions, the intermediate has a very short lifetime. Moreover, this theory is based off of classical mechanics, so does not take into account that some reactants that do not have enough energy to overcome the barrier are able to 'tunnel' through the barrier, this is a quantum principle that is not accounted for. Additionally, at higher temperatures more transition states become available as more states of energy such as vibrational, rotational and translational are becoming possible; this should be an issue as the pre-exponential factor in the Transition State Theory is dependent on temperature.
Great discussion. What about your finding above, is there an assumption stating once the TS has been crossed and formed products it cannot return to reactants. Your finding defies this...how do you think this would affect the rate of reaction?Mys18 (talk) 02:06, 23 May 2020 (BST)
Exercise 2: F-H-H system
Q1: By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
F+H2 is an exothermic reaction while the H+HF reaction is endothermic. The potential energy surface shows this as when distance BC is small, the potential energy is lower showing that the H-F bond energy is greater than that of H-H. Vice versa, when BC distance is large, the potential energy is higher. Where A is H, B is H and C is F. The BC distance represents the atom F approaching the H2 so the potential energy decreases then after the collision, BC distance increases showing how the H atom moves away from the HF molecule.
Perhaps scout the literature for experimentally determined H-F and H-H bond strengths to further support your conclusions. Mys18 (talk) 02:08, 23 May 2020 (BST)
Q2:Locate the approximate position of the transition state.
The transition state is where the total momentum is zero as there is minimal to no movement of the species; therefore, using similar methods as the those used in the H+H2 system the transition state was calculated to be at H-H distance =74.4pm and H-F distance= 181.1. The energy vs time and contour plots above support this.
Q3: Report the activation energy for both reactions
According to Hammonds Postulate, as the transition state has a very short lifetime, it is closer in molecular structure to reactants. Consequently, with a slight alteration in H-H distance(from 74.4 to 75.4), the MEP will show a movement towards the reactants (H-H and F).
The plot above shows the contour plot for the trajectory of H2+F from the transition state, the difference in potential energy in the energy vs time plot above shows the activation energy. In this reaction the activation energy of H-H+F->F-H+H=15.593 kJ/mol.
The plot above shows the contour plot of the trajectory of HF+F from the transition state, . In this reaction the activation energy of F-H+H->H-H+F=123.457 kJ/mol.
You Ea for F + H2 --> HF + H is quite larger (I would expect between 1 - 1.5 kJmol-1) It is tricky to see how you calculated this as the full calculation has not been reported.Mys18 (talk) 02:16, 23 May 2020 (BST)
Q4:Identify a set of initial conditions that results in a reactive trajectory for the F + H2, and look at the “Animation” and “Momenta vs Time”. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.
Using the set of conditions where H-H distance is 74.4pm and H-F distance is 190pm where both momenta are at -1, a graph of momenta vs time is produced, as shown below:
It can be seen that after the collision, the momentum of the H-F oscillates rapidly showing the vibration of this bond, this is because this reaction pathway is exothermic( referring to the activation energy previously calculated). Due to the conservation of energy, any energy released would be converted into vibrational energy in the H-F bond. This could be confirmed experimentally by reacting some Hydrogen gas in a vessel with Fluorine, if the energy is converted into vibrational energy, this would generate heat and consequently, the reaction vessel would heat up as its temperature increases. This temperature increase could be measured using a thermometer.
We could use a thermometer, but there are many factors which could then influence our temperature reading, heat loss to surroundings etc. calorimetry would be a more controlled technique. Additionally how about IR spectroscopy for vibrational energy? Mys18 (talk) 02:23, 23 May 2020 (BST)
Q5: Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
After testing out various values of momenta(keeping p(H-F)=-1), it was discovered that when p(H-H) is larger than +0.6, the collision was not successful as shown below:
Negative values of momenta were also unsuccessful:
However, values between and including 0 to +0.6 were successful:
Consequently, the reactions that were successful were those where the approaching atom had a small momentum, due to the smaller activation energy. When the reaction did not succeed, it was due to how the close proximity of the H atom to the vibrating transition state breaking the H-F bond straight after its formation. Moreover, if the H2 molecule starts off with too much momentum, this bond could break.
On the other hand, for the reverse reaction of F-H+H-> H-H+F, Hammonds Postulate would suggest that the transition state is closer to the products, so it is required for the incoming H atom to have a large momentum that is able to overcome the larger activation energy. However, if the H-F bond has too much initial vibrational energy, the collision of the H atom could possibly not be strong enough to cause a change in momentum in the H-F bond, meaning it will not break. Therefore, a low initial vibrational energy in the H-F bond is optimal.
Polanyi's rules explain how the position of the barrier affects the energy requirement in a colllision. For an exothermic reaction like the H-H+F->H-F+H reaction, the reaction barrier (transition state) is closer to the reactants. According to Polanyi's rules, the reactant translational energy is more effective than vibrational energy to overcome the barrier, then increasing the reaction rate. The opposite is true for the endothermic F-H+H->H-H+F reaction. This means that for an early barrier(exothermic) reaction, the energy will mainly be converted into vibrational energy; whereas for a late barrier (endothermic) reaction, the energy will mainly be converted into translational energy[1].
Bibliography
- Yan, Shannon et al. “Tracking the energy flow along the reaction path.” Proceedings of the National Academy of Sciences of the United States of America vol. 105,35 (2008): 12667-72. doi:10.1073/pnas.0800220105