MRD:01413765 zl6417

Molecular Reaction Dynamics

Ng611 (talk) 20:59, 12 May 2019 (BST) Overall, not a bad report. Overall, more detailed discussion and explanation would have improved this report further. Your first section was lacking detail in one or two places, and section 2 had one or two mistakes as well.

EXERCISE 1: H + H2 system

On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?

1). The transition state is mathematically defined as the saddle point on the potential energy surface. At the saddle point the potential is maximum for the reaction path, while for the path orthogonal to the reaction path, the potential is at the minimum value. Mathematically, the first derivatives of the potential at the saddle point are:

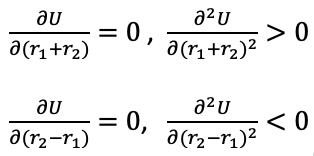
Transition states can be identified by mathematical calculations of the two first derivatives. Unlikely a local minimum on the potential surface, the saddle point which represents the transition state is a maximum on the minimum energy path linking reactants and products.

Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

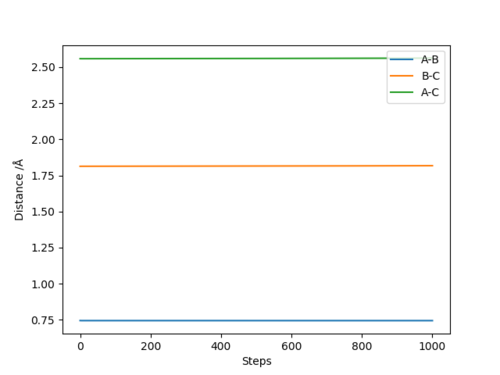
2). Best estimate of r_ts= 0.908 Å

The internuclear distance vs time plot calculated by Dynamics is a horizontal line at the transition state

By plotting potential energy vs intermolecular distance, the distance corresponding to the minimum value of potential energy is r_ts and is equal to approximately 0.908 Å

Ng611 (talk) 20:41, 12 May 2019 (BST) Some additional explanation here would be helpful. How have you determined that this stationary point is a maximum along the MEP and not a minimum (Both would yield flat trajectories)? What constraints did you put on your system (if any?)

Comment on how the mep and the trajectory you just calculated differ.

3) Both trajectories give the product. For Dynamics, the trajectory shows there is vibration between the two hydrogens in the product. Whereas for MEP, there is no vibration, the reason being that the momenta/velocities of the atoms are always reset to zero in each time step.

Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?

4)

p₁	p₂	E_tot/kcal mol^-1	Reactive?		Description of the dynamics
-1.25	-2.5	-99.02	YES	p1=-1.25, p2=-2.5	H_A approaches H_B-H_C, the product H_A-H_B forms and then moves away from H_C
-1.5	-2.0	-100.46	NO	p1=-1.5, p2=-2.0	H_A approaches H_B-H_C firstly, but then moves away and no product forms
-1.5	-2.5	-98.96	YES	p1=-1.5, p2=-2.5	H_A approaches H_B-H_C, the product H_A-H_B forms and then moves away from H_C
-2.5	-5.0	-84.96	NO	p1=-2.5, p2=-5.0	H_A approaches H_B-H_C, the product H_A-H_B forms but then dissociates and the reactant reforms before H_A moves away
-2.5	-5.2	-83.42	YES	p1=-2.5, p2=-5.2	H_A approaches H_B-H_C, the product H_A-H_B forms but then the reactant reforms, before the product forms again and moves away

Conclusion:

Whether the trajectories starting with the same positions would be reactive or not is dependent on the values of momenta, that is, the two momenta p₁ and p₂ have to be within a certain range respectively.

Higher kinetic energy of the reactant would not guarantee the formation of a stable product and may lead to the dissociation of the product.

Based on the table above, if the kinetic energy of the attacking H_A is not big enough, the reaction would not take place. Whereas if the kinetic energy of H_A is too big, the product may dissociate and the reactant would reform.

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

5) Main assumptions of Transition State Theory¹

Electronic and nuclear motions are separated.
The reactant molecules are distributed among their states in accordance with the Maxwell-Boltzmann distribution.
Molecular systems that have crossed the transition state to products cannot turn back and reform reactants.
In the transition state, motion along the reaction coordinate may be separated from the other motions and can be treated classically as a translation.
Even without an equilibrium between reactant and product molecules, the transition states that are becoming products are distributed among their states according to the Maxwell-Boltzmann laws.

In experiments, there is a phenomenon called barrier crossing, that is after the product is formed the system might recross the transition state region and reform the reactants. This is in contrast with the third assumption of Transition State Theory listed above. Two examples of barrier crossing are shown in the last two examples above in the form.

Ng611 (talk) 20:43, 12 May 2019 (BST) How does this affect the quantitative accuracy of TS theory? Is it likely to overestimate or underestimate the true rate of reaction?

EXERCISE 2: F - H - H system

PES inspection

Bond energy

H-H 104 kcal/mol

H-F 135 kJ/mol

F + H₂ -- HF + H

Exothermic because the bond energy of H-F is larger than that of H-H. The energy released due to formation of the stronger bond H-F is greater than the energy consumed by breakage of H-H bond.

H + HF -- H₂ + F

Endothermic because the bond energy of H-H is smaller than that of H-F. The energy consumed by breakage of H-F bond is greater than the energy released by the formation of the product.

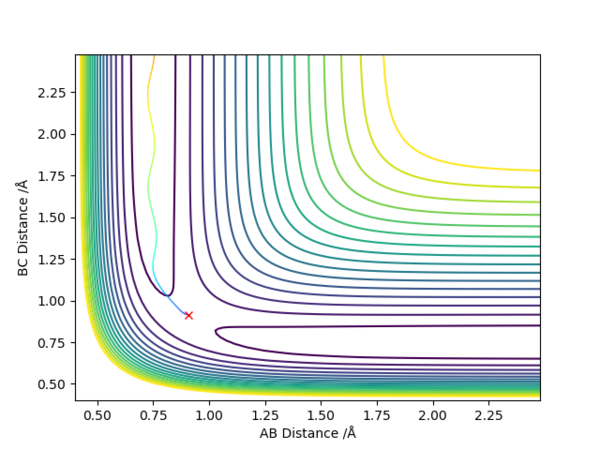
The transition state can be determined by calculation o of trajectory by MEP. The starting intermolecular distances which do not change with steps are transition state positions, because there is no gradient at transition state point. Besides, the trajectory is a stationary point on the contour plot.

At the transition state, the H-H distance is around 0.7452 Å, H-F distance is around 1.8132 Å.

Contour	Internuclear Distance

The two activation energies can be calculated by looking into the total energies of the system. The calculation can be done by locating the atoms slightly away from the transition states, and the difference between the two plateaus in the energy diagrams below is the activation energy.

The reaction F + H₂ -- HF + F involves breakage of the H-H bond, which is supposed to have a smaller activation energy than that of breakage of H-F. The reason is that the bond energy of H-H is smaller than that of H-F.

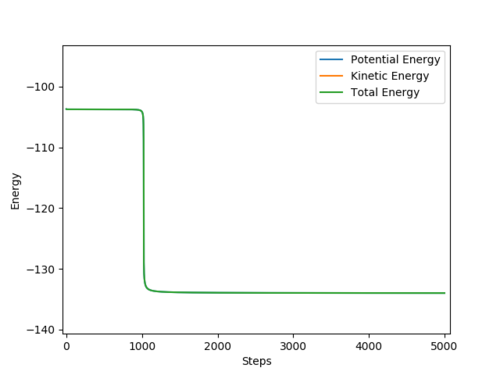F + H₂ ( H-H: 0.7446 Å, H-F: 1.8126 Å, Steps: 5000/ 0.004)	H + HF ( H-H: 0.7352 Å, H-F: 1.8132 Å, Steps: 5000/0.002)

Ng611 (talk) 20:50, 12 May 2019 (BST) Looking at your system, it seems that you haven't reached the true minimum for your F + H2 TS energy. Coarsening your timestep even further may help. Another option would be to run a dynamics calculation, fin the time the energy was at its local minimum and correlate that with the internuclear distances.

Activation energy:

F + H₂ -- HF + F        0.214 kcal/mol

H + HF -- H₂ + F        31.111 kcal/mol

Reaction dynamics

In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally

For the reaction F + H₂, F approaches H with a certain kinetic energy, after reaction the vibrational energy of the product is released to the environment, which is likely to take the form as heat. The measurement of the heat generated can confirm this mechanism

Ng611 (talk) 20:52, 12 May 2019 (BST) Heat generation wouldn't distinguish between kinetic energy due to vibrations or translations. What else could you do?

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Reactions generally have either an early transition state (that is, a transition state resembling the reactants), or a late transition state (that is, a transition state resembling the products).

For a late transition state, vibrational energy is more efficient in promoting the reaction than transitional energy. Whereas the reverse is true for an early transition state.

• F+H₂ has an early transition state. Hence high transitional energy, that is high kinetic energy of the incoming F atom promotes the reaction even with little vibrational energy in the H₂;

• H+HF has a late transition state. Therefore high vibrational energy in HF promotes the reaction even with little kinetic energy of the incoming H atom.

F+H₂
H+HF

Ng611 (talk) 20:53, 12 May 2019 (BST) Good examples, well done.

Reference

[1] J. I. Steinfeld, J. S. Francisco, W. L. Hase, Chemical Kinetic and Dynamics, Prentice-Hall, New Jersey, 1998

[2] John C. Polanyi, Accounts of Chemical Research, 1972, DOI: 10.1021/ar50053a001