MRD:01409307

EXERCISE 1: H + H2 system

Q1

A potential energy surface is a conceptual tool for supporting the analysis of molecular geometry and chemical reaction dynamics. Some special points can be classified according to the first and second derivatives of the energy with respect to position, which provides values of the gradient and the curvature. Stationary points (∂V(r_i)/∂r_i=0) have physical meanings, the energy minima correspond to physically stable chemical species and the saddle points correspond to transition states.

Therefore, the transition state can be determined mathematically. A saddle point is characterized by a negative curvature in one direction and positive curvature in all other directions. At both minimum point and saddle point, the slope of the function must be zero.

$(d f / d x)_{y} = 0$ , $(d f / d y)_{x} = 0$

The physically stable form which is at the minima should fulfil the requirement below. In this case, the second derivatives are positive, due to positive curvature.

$(d^{2} f / d x^{2})_{y} > = 0$ , $(d^{2} f / d y^{2})_{x} > = 0$

However, the transition state which sits at the saddle point has a slightly different equation, one of the second derivative is negative which indicates the negative curvature, and all other derivatives are positives.

$(d^{2} f / d x^{2})_{y} (d^{2} f / d y^{2})_{x} < = 0$

The transition state is a critical point which is different from a local minimum. It can be a relative minimum along one axial direction and a relative maximum along the crossing axis, while a local minimum is only considered in one direction.

Good, but the second partial derivative is either less than or more than zero for the local maximum and minimum, respectively, not equal to zero. Sf3014 (talk) 14:55, 15 May 2019 (BST)

Q2

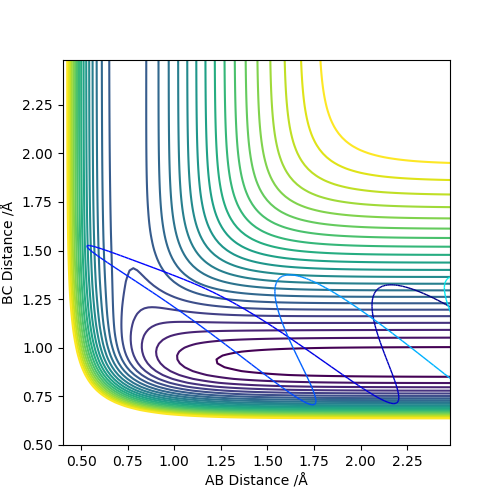
The simulation condition was set to be r1=2.3, r2=0.74, p1=-2.7, p2=0.

There is a crossing point of two internuclear distance against time plots, the value was estimated to be 0.9167 Å.

Another simulation was carried out using MEP method. The parameter set was r1=r2=1.25, p1=p2=0.

The minimum potential energy data exported indicates the position of the transition state. Thus r_ts=0.9077 Å. Good explanation, next time show the information from the new calculation since you stated it. Also, if you showed the internuclear vs time graph for the parameters at the transition state, you can back up your statement. Sf3014 (talk) 15:05, 15 May 2019 (BST)

Q3

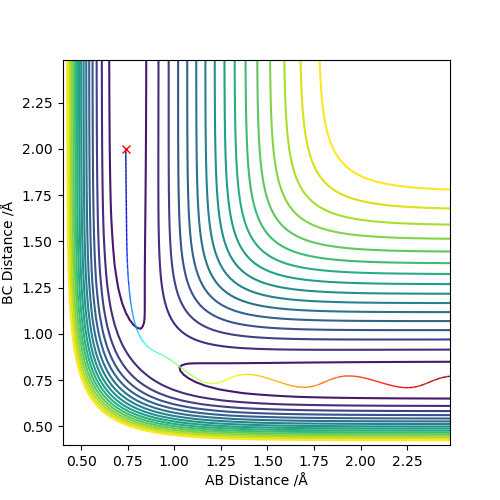
The MEP method and Dynamics method are used and the parameters are set to be r1=0.9177, r2=0.9077 and p1=p2=0.

In MEP method, the kinetic energy (momentum) is always set to be zero, indicating the velocity, momentum and vibration motion of the molecule disappeared during the reaction. Therefore, the total energy is not conserved. However, in Dynamics method, the kinetic energy is conserved and the vibration motion can be seen on the Contour Plot where the plot fluctuates. Good comparison, but how do you know that the momentum and vibration has disappeared during the reaction? Also, you mentioned that the kinetic energy is conserved in the dynamic calculation, but your graph only shows for the transition state to the products not the whole reaction. You can show that the momentum is zero using the momenta vs time graph. Sf3014 (talk) 15:16, 15 May 2019 (BST)

Q4

p₁	p₂	E_tot	Reactive?	Description of the dynamics
-1.25	-2.5	-99.0184	Yes	Atom C approaching the molecule AB, the new product formed and moved away.
-1.5	-2.0	-100.456	No	Atom C approaching the molecule AB, but with insufficient translation kinetic energy thus no products formed.
-1.5	-2.5	-98.955	Yes	Atom C approaching the molecule AB, with sufficient translation kinetic energy thus formed the product.
-2.5	-5.0	-84.956	No	Atom C approaching vibration excited molecule AB, the transition state has been reached due to high kinetic energy but product dissociated.
-2.5	-5.2	-83.416	Yes	Atom C approaching vibration excited molecule AB, the transition state has been reached due to high kinetic energy and product reformed after dissociation.

The Contour plot of Molecule at p₁ = -1.25 and p₂ = -2.5

The Contour plot of Molecule at p₁ = -1.5 and p₂ = -2.0

The Contour plot of Molecule at p₁ = -1.5 and p₂ = -2.5

The Contour plot of Molecule at p₁ = -2.5 and p₂ = -5.0

The Contour plot of Molecule at p₁ = -2.5 and p₂ = -5.2

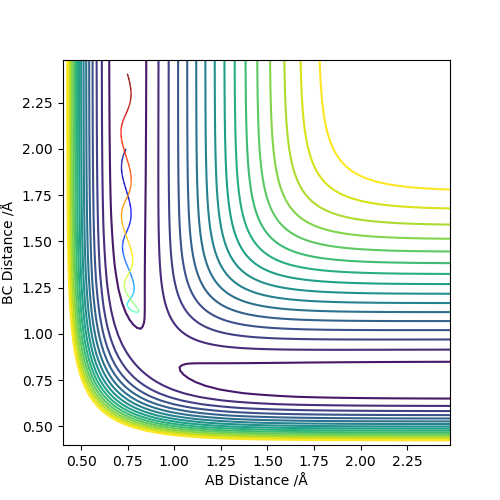
It can conclude that whether the trajectories are reactive or not starting from the same positions is not dependent on the values of momenta, however, the range of two momenta p1 and p2 is dominant respectively. The higher kinetic energy of the reactant may not only support the formation of a stable product but also cause an excessive collision of atoms which initially forms the product and then being dissociated. Good observation and clear layout. Sf3014 (talk) 15:21, 15 May 2019 (BST)

Q5

There are five main assumptions of Transition State Theory.

(1) Electronic and nuclear motions are separated.

(2) The reactant molecules are distributed among their states in accordance with the Maxwell-Boltzmann distribution.

(3) Molecular systems that have crossed the transition state in the direction of products cannot turn around and reform reactants.

(4) In the transition state, motion along the reaction coordinate may be separated from the other motions and treated classically as a translation.

(5) Even in the absence of equilibrium between reactant and product molecules, the transition states that are becoming products are distributed among their states according to the Maxwell-Boltzmann laws.

As the product reform back to the reactant which conflicts with the first assumption in the fourth reaction, it may lead to the decrease in the rate of the reaction. Moreover, other assumptions cannot be verified due to insufficient experimental results. Well done but you need to reference, where did you get this information from? Also, what may lead to a decrease in the reaction rate? Is it the assumptions made in transition state theory? You should avoid saying "it" if what you are referring to hasn't been mentioned for a while. Sf3014 (talk) 15:34, 15 May 2019 (BST)

Exercise 2: F - H - H system

Q6

Type of reaction	Energetic	Bond Strength	Position of Transition State
F + H₂ → HF + H	Exothermic	formation of HF bond (-565 kJ/mol) and breaking H₂ bond (+436kJ/mol)	r1 = 1.8126, r2 = 0.7446
H + HF → F + H₂	Endothermic	formation of H₂ bond (+436KJ/mol) and breaking HF bond (-565 KJ/mol)	r1 = 0.7446, r2 = 1.8126

The Transition Point of Molecule F + H2 by Contour Plot	The Transition Point of Molecule HF+H by Contour Plot

Good, but you needed to use the potential surface and describe which direction is exo- or endo- thermic as well as the bond energies. Also, it would of been great to provide some explanation on how you located the position of the transition state using Hammond postulate. Sf3014 (talk) 15:40, 15 May 2019 (BST)

Q7

	Type of Reaction	Activation Energy
F + H₂ → HF + H	Exothermic	0.22 kcal/mol
H + HF → F + H₂	Endothermic	31.16 kcal/mol

The Activation Energy of Molecule F + H2 by Contour Plot	The Activation Energy of Molecule H + HF by Contour Plot

Good, but some description on how you worked out the activation energy would be great. Sf3014 (talk) 15:49, 15 May 2019 (BST)

Q8

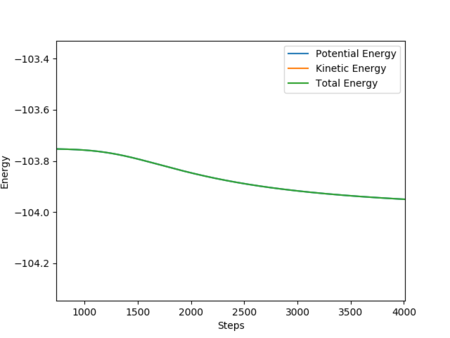
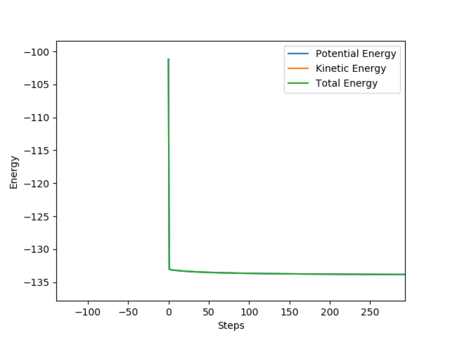
The initial condition of the estimation is r1 = 1.8126 and r2 = 0.7446, p1= -0.7 and p2 = -0.1 (Atom A is F in this simulation)

The Reaction pathway of F + H2	The Energy Change of reaction F + H2	The changing momentum of F + H2

After the product was formed, the potential energy decreased and the kinetic energy increased. The increased kinetic energy was transferred by generating heat. This can be observed from the increasing temperature of the reaction mixture. The H-H bonding has vibrational energy before the collision. After the reaction, the formation of the H-F bond which provided the excess energy led to the vibration energy of HF molecule. Therefore, the intermolecular momentum of H₂ flattened and the momentum of HF was vigorously oscillating. This can be observed from changing the vibration state. Good explanation, but it would be great if you stated analytical techniques that will measure the changes you mentioned. Sf3014 (talk) 15:54, 15 May 2019 (BST)

Q9

The Higer Vibration and Lower translation Energy of HF + H	The Lower Vibration and Higher translation Energy of HF + H
The Lower Vibration and Higher translation Energy of F + H2	The Higer Vibration and Lower translation Energy of F + H2

Type of reaction	Type of transition state
F + H₂ → HF + H	ealier transtion state
H + HF → F + H₂	later transtion state

It is reported that the location of the energy barrier plays an important role in selecting the distribution of reactant energy most likely to lead to reaction. Translational energy is most effective for passage across an 'early' barrier in the entrance channel, whereas reactant vibrational energy far in excess of the barrier height may be ineffective for reaction. Conversely, a 'late' barrier is best surmounted by vibrational rather than translational energy in the reactants. In the case of the early barrier, a vibrationally excited molecule is just too busy rattling from side to side and does not have enough energy left to reach the top of the barrier. In the late barrier case, vibrationally excited molecules with the correct phase can find their way to the top of the barrier.

For endothermic reactions the transition state resembles the reaction products according to the Hammond's postulate. In the endothermic case this implies that the maximum of the potential barrier occurs in the product channel (late barrier), so that vibrational energy in the reactants will be more effective than translational energy in crossing the barrier. Good statement, but how does this compare to the contour plots shown? Also, you started you sentence with "It is reported...", reported where? Statements like that should always be backed up with references. Sf3014 (talk) 16:00, 15 May 2019 (BST)