Reactional Dynamics

EXERCISE 1: H + H₂ system

Finding the Transition State Mathematically

The transition state on a potential energy surface plot is mathematically defined as the point along the reaction pathway were ∂V(r_i)/∂r_i=0, where i = r₁ and r₂ i.e. the gradient in any direction at that point is zero (meaning that if a molecule were placed directly on it, it would be stable and wouldn't react). But more than that, the transition state is also a saddle point (the maximum in a minimum energy pathway), which can be defined mathematically by computing the function's Hessian matrix (square matrix of second order differentials. If said matrix is indefinite at a certain point, then that point must be a saddle point, and hence a transition state for a reaction. More simply, a saddle point can be distinguished from a local minimum (∂V(r_i)/∂r_i=0), by looking at the second order differentials ∂V²(r₁)/∂r₁², and ∂V²(r₂)/∂r₂². Only if one of these secondary derivatives is less than 0, and the other is greater than 0 are we dealing with a saddle point. If both are greater than 0 the point is a local minimum, and if both points are less than 0 the point is a local maximum (and the reaction could proceed in many different directions).

Ng611 (talk) 16:31, 7 June 2019 (BST) Dubious about your description of the hessian matrix. What do you mean by indefinite?

Finding the Transition State with the Simulation

The coordinates of the transition state must be symmetric for our 3 homogenous atoms that collide linearly, and were found to be 0.908 Å.

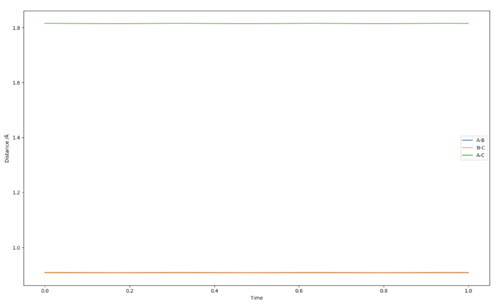
A plot from the simulation showing internuclear distance vs time with starting conditions near the transition state

As stated previously, the transition state is a saddle point in the potential energy surface, and hence the gradient in any direction at that point is zero. Therefore, if the particles were placed directly onto that point, they would not move as they are at a minimum, and no oscillations would bee seen. So to locate the transition state, the simulation was simply run with the starting conditions of both bonds being equal in length, and none of the particles having any momentum. Thus, any change in internuclear distances could only be due to oscillation occurring as the particles loose potential energy and gain kinetic energy, and vice versa (because the chosen starting point had a non-zero slope i.e. was not the transition state). The initial bond lengths were then varied until the graph above was produced, at 0.908 Å, where the internuclear distances are almost constant, suggesting that this is a distance very close to the transition state.

MEP vs Dynamic Trajectory

MEP potential energy contour plot with reaction trajectory

Dynamic potential energy contour plot with reaction trajectory

Dynamic potential energy surface plot using position and momenta values at t= 2.0

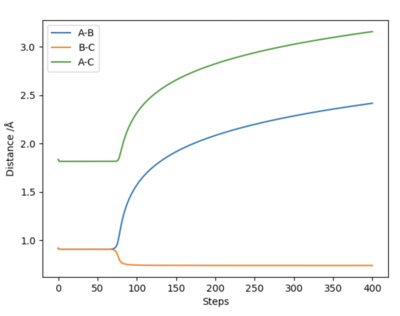
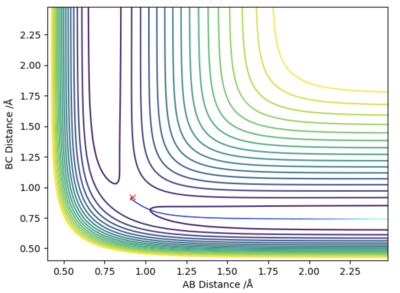
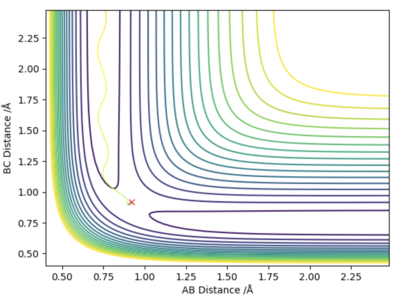
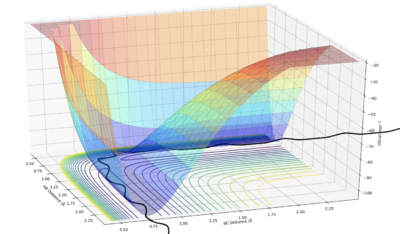
The main difference between the dynamically calculated trajectory and the minimum energy path (MEP), is that the MEP trajectory resets the velocity to 0 after every time step, and as a result the momentum of the bonds is always equal to zero (i.e. it does not account for vibrational energy). On the left hand side, internuclear distance vs time, and a contour potential energy plot for the MEP calculation method are shown, in contrast to the right hand side, with shows the same plots but using a dynamic calculation method which accounts for inertia. It can be seen that on the right hand side bond oscillations occur (as they should), whereas on the left hand side, using the MEP calculation method there are no oscillations, which was expected as the momentum must always be zero, and furthermore, as the velocity is always reset, the particle that moves away from the bond gets slower and slower as the potential surface flattens out to zero, until it will no longer be affected by any internuclear effects, and stand completely still (at roughly 5.6 Å).

Changing which atom is initially displaced slightly further from the transition state changes the atoms that end up bonded together. As expected, the atom that is closer to the transition state ends up forming a bond, whereas the other one is expelled and moves away.

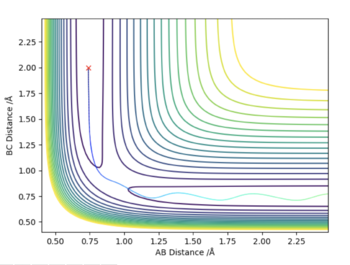
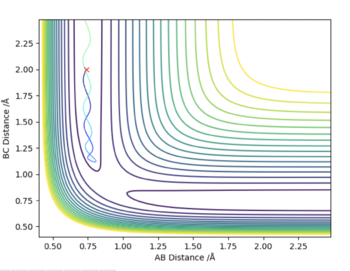
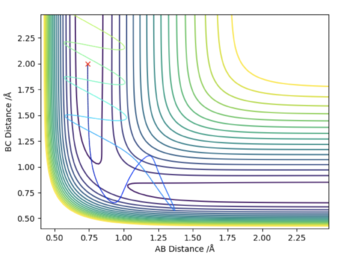
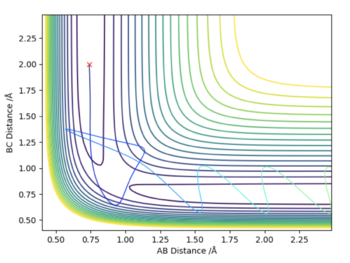
Interestingly, if one takes the final internuclear distance after 2 seconds, as well as the average momenta of the particles, and puts them in as initial conditions except with opposite momenta, then at times the reverse collision proceeds, and as the particles approach the other two hydrogen atoms combine. But other times, when using slightly different starting conditions (due to the fact that the values gathered from the simulation plots are not very precise), the particles collide, but this time the same two atoms stay bonded together, and they simply collide at the transition state, bounce of each other, and do not react moving apart the way they came from, showing that only a slight change in conditions can have a very different outcome.

One would think that anything that has starting conditions following the MEP trajectory would lead to the formation of a new product, however, some of the time, as stated above, the reactants just bounce off one another and no reaction occurs. This seems to be the case when the difference in momentum is too high, and the bond strength is no longer strong enough to cancel out the excess momentum, or when the difference in momentum is too low, so that the momentum of the particles is not enough to overcome the electrostatic repulsion. In general, the reacting pathway could be worked out from the MEP through the simulation, by experimentally finding the minimum and maximum momentum difference that allows for the reaction to proceed along the MEP. It is important to note that for a given position on the potential energy surface, a less negative total energy means a higher, more positive kinetic energy (as total energy = potential energy (which at a given point is fix and negative) + kinetic energy (which depends on momentum and is positive)).

Reactive and Unreactive Trajectories

p₁	p₂	E_tot	Reactive?	Description of the dynamics
-1.25	-2.5	-99	Yes	The particles have enough energy to overcome the electrostatic repulsion, collide and the reaction occurs. It is interesting to note, that since the original H₂ molecule has half the momentum of the free particle with one of the atoms of the molecule. This is only possible if the molecule does not have any vibrational motion, as can be seen by the contour plot. However, after the collision the momenta change and the molecule starts to vibrate.
-1.5	-2.0	-101	No	The particles do not collide because the total energy is not enough to overcome the electrostatic repulsion, so before reaching the transition state the particles are pushed apart and go back the way they came.
-1.5	-2.5	-99	Yes	The particles have slightly more energy than the minimum required for the reaction to occur. Hence they collide, react, and both initial and new H₂ molecules have vibrational energy (slightly more than for the first case).
-2.5	-5.0	-85	No	The particles have too much energy, so that when they collide, although initially it seems like they have reacted, the first particle bounces back and the H₂ bond strength is not enough to keep it bound, so the molecule dissociates and the reactant go apparat the way they came.
-2.5	-5.2	-84	Yes	According to the theory that was presented before, one would expect that since the particles have more energy than the maximum possible kinetic energy they should not react, but they do. This is because this energy gives rise to a special case. From the contour plot it can be seen that particle 2 collides with the H₂ molecule, thereby breaking the pre-existing bond. Due to the excess energy this molecule then dissociates, and the previous H₂ molecule is formed. However the kinetic energy from the collision is still in excess of the maximum possible binding energy, so the H₂ molecule dissociates again, and collides with particle 2. However the particle transferred some of its kinetic energy to the other particle during the previous collision, and as a result it now has less kinetic energy and can form a bond with particle 2. Hence the reaction does proceed.

From the table above we can conclude that the hypothesis presented beforehand seems to be confirmed by the simulation, however there are a few exceptions. At certain energies above the 'maximum' possible energy that allows for bonding (as particles that have more energies will collide, and dissociate because their energy is too high to be contained by the bond, as can be visualised using the Lennard-Jones potential) the reaction still proceeds unexpectedly. This is due to the fact that the particles rebound off one another, the original H₂ molecule is formed again, but the energy is high enough that it dissociates again, collides with the second particle (this time with lower energy as some of it's kinetic energy was transferred to the other particle during the previous collision) forming a bond and the reaction proceeds.

Transition state Theory and its applicability

The main assumptions of transition state theory are that all collision are completely elastic, meaning that the total kinetic energy of the system must be conserved. It also assumes that the activated complex is in a special quasi equilibrium with its reactants (the reactants form an equilibrium with the activated complex, which can then decay to form the products), and that the rate of reaction can be calculated using kinetic theory from the conversion of the activated complex to the products. Lastly, it also assumes that the reactions take place classically, and that no tunnelling is involved (which is especially relevant for hydrogen reactions).¹

The Eyring equation is used to describe the rate of reaction under the assumption of transition state theory. It states that:

                                                                          $k = \frac{κ k_{B} T}{h} e^{- \frac{Δ^{‡} G^{⊖}}{R T}}$

Where $k$ is the reaction rate constant, κ is the transmission coefficient (i.e. the relation of how much of the vibrational frequencies will be transmitted across the transition state, and is often assumed to be 1), k_B is the Boltzmann constant, h is Planck's constant, and Δ^‡G^Θ is the standard Gibbs free energy of the transition state (also equal to ΔH-TΔS).

Assuming that we have a reaction of this type:

                                                                           A + B ⇌ C^‡ → P

Where the activated complex undergoes unimolecular decay to give the products, it follows that the rate of reaction is equal to:

                                                                             $v$ =  $k$ [A][B]

¹ Using these formulas it is possible to calculate a value for the rate constant. Assuming that our gasses are ideal, it is known that the kinetic energy K.E = $\frac{3}{2}$ k_BT for a single molecule, and that the standard Gibbs free energy of activation is equal to Δ^‡G^Θ= ΔH-TΔS (however in our case the products and reactants have exactly the same entropy so ΔS must be equal to 0, and hence Δ^‡G^Θ= ΔH). ΔH was found by using starting conditions with the minimum amount of possible kinetic energy that still proceed to react (meaning that they should have a maximum kinetic energy equal only slightly more than the potential energy of the transition state), which was found to be -100 Kcal.mol^-1, and the minimum potential energy far away from the transition state, found to be 104 Kcal.mol^-1. Converting this to joules this means that Δ^‡G^Θ= ΔH = 17 KJ.mol^-1.

If we plug these values into the equation, then we get that at standard temperature (273.15K, which is only equal to 3.4 KJ.mol^-1 of kinetic energy) the rate constant is equal to 3.2*10⁹ s^-1. This is a very large value, meaning that this reaction takes place very quickly, as expected because the activation energy is low.

Unfortunately, literature rate constants for this reaction could not be found, however one would expect them to be higher than those determined following transition state theory, as this reaction has a very low transition state and only involves hydrogen atoms, meaning that it has the perfect set up to allow for tunnelling, which will speed up the reaction as even hydrogen atoms that don't have enough kinetic energy to overcome the activation barrier could simply tunnel through it to form the products.

Ng611 (talk) 16:33, 7 June 2019 (BST) What about the effect of TS recrossing (for example, in the trajectories you provided above?)

EXERCISE 2: F - H - H system

PES Inspection

By looking at the potential energy surface of the F - H - H system it is clear that the reaction F + H₂ is exothermic, because the potential energy of the products is lower than that of the reactants, while it must be the opposite way around for the reverse reaction H + HF, which is endothermic. This was to be expected because the Hydrogen - Fluorine single bond is much stronger than the Hydrogen - Hydrogen bond (because Fluorine is very electronegative, making it a very ionic bond, held together by electrostatic attraction, and because Fluorine is very small as it has a high nuclear charge), meaning that HF is very stable, and breaking that bond requires a lot of energy, which is not regained when forming the HH bond, making it an endothermic process that requires energy. HF has a bond energy of 565 KJ.mol^-1, whereas HH only has a bond energy of 432 KJ.mol^-1.²

To find the transition state, we first find the bond length of both HH and HF to give us an idea of where to look. The equilibrium bond length is reached if we input it as our starting bond length and the molecule doesn't oscillate (meaning no net force is acting on the molecules, meaning they are in equilibrium). For HH it was found to he 0.742 Å, and for HF it was found to be 0.920 Å. Remembering Hammonds postulate, which states that the transition state resembles most either reactants or products depending on which is closer in energy. If we look at the reaction of F + H₂, we know that it is exothermic, and hence the reactants most closely resemble the transition state. Hence it will also be an early transition state, and should be close to hydrogen equilibrium bond length, and the fluorine being further away. The plot on the left shows that a transition state has been reached when the HH bond distance is 0.74488 Å and the HF bond distance is 1.810692 Å because when they are input as initial coordinates the molecules stay stationary, but when a parameter is slightly changed they move with kinetic and vibrational energy, suggesting that a saddle point (transition point) has been found.

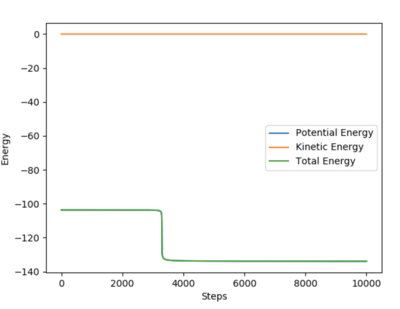
Finding the activation energy for both reactions isn't very easy as the transition state is only very slightly higher in potential energy than the exothermic reactant (F + H₂). Using the MEP calculation method, and by selecting an H₂ bond distance that was slightly shorter than the transition state the reaction to form the products proceeded. By only disturbing the system ever so slightly and using a very short step length (0.001) we were able to approximate the transition state energy as well as the energy of the products, which can be seen on the far right of the plot on the right. The same was done for the other products, by slightly increasing the H₂ bond length. Finally, in order to check the values we got, the transition state distances were input and under the Initial Geometric Information section (seen on the table on the left) the initial potential energy is given (which must be that of the transition state since we used it as our initial conditions). The results obtained were that the more stable products had a potential energy of -133.702, the less stable products had a potential energy of -104.018, and the transition state had a potential energy of -103.752 (all measured in Kcal.molmol^-1). Converting to SI units and taking the difference gives an activation energy of 125.31 KJ.mol^-1 for the reaction H + HF → F + H₂, and an activation energy of 1.11 KJ.mol^-1 for the reaction F + H₂ → H + HF.

Ng611 (talk) 16:35, 7 June 2019 (BST) Good!

Reaction Dynamics

By doing the same thing as in exercise 1, and inputing the final values of a dynamical calculation starting at values close to the transition state, only with reverse momentum, we get a set of initial conditions that lead to the reverse collision (HH bond distance = 0.745, HF distance = 2.5, momentum HF = -1, and momentum HH can take values between -0.3 and -0.7). During this reactions, after having passed the transition state, the excess potential energy is converted into kinetic energy as the particles accelerates due to the attractive electrostatic forces between the Hydrogen and the Fluorine. This kinetic energy is then reconverted into potential energy as the Hydrogen and Fluorine atoms get too close to each other and start to repel. With enough starting momentum (i.e. at a high enough temperature) the excess kinetic energy could mean that during the collision of particles, excited HF vibrational states could be populated. This excited species could then emit infrared radiation as it decays back down to its ground state, or it could undergo vibrational relaxation, converting the vibrational energy into thermal energy (i.e. back into kinetic energy).³

Experimentally, this mechanism could be determined using infrared chemiluminescence, and by studying the emission spectrum resulting from emitted photons one can calculate the population of the different vibrational energy levels. Also measuring the temperature of the solution allows us to see if the average kinetic energy of the particles has increased due to the attractive forces of the Lennard-Jones potential, or due to vibrational relaxation occurring and being converted into thermal energy.¹

Ng611 (talk) 16:36, 7 June 2019 (BST) Excellent!

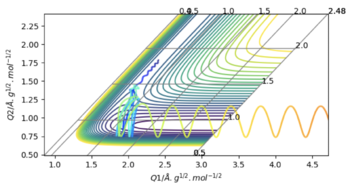
Using starting coordinates of 0.74 for the HH bond and 1.83 for the HF bond (which is quite close to the transition state), several simulations were run with significant energy input into the system (much more than the activation energy), to see how the reaction would progress.

p₁	p₂	E_tot	Reactive?	Description of the dynamics
-3	-0.5	-96	Yes	The Hydrogen molecule now has significant vibrational energy as well as kinetic energy, which leads to an interesting scenario after the first HF collision. By thinking of our particles like two Lennard-Jones potentials on either side of the Hydrogen which overlap in the middle, as seen in the graph on the right. Because the Hydrogen atom has significant kinetic energy, it is able to oscillate between these two potentials. However, the other atoms are not fixed in space, the Fluorine is quite heavy so that collisions with the Hydrogen cause a negligible change in it's momentum. The other Hydrogen atom however is repelled after each collision (but also attracted by electrostatic forces to the other hydrogen so that it gets pulled back). These oscillations take place several times, until the oscillating Hydrogen has given enough kinetic energy to the other Hydrogen for it to move away, and for itself to stay bound to the Fluorine.
-2	-0.5	-101	Yes	The same reaction dynamics occur at this energy, only that because less vibrational and kinetic energy has been put into the system, less oscillations occur because the oscillating Hydrogen quickly stays bound to the Fluorine.
-0.6	-0.5	-103	Yes	This is a very interesting, special case. Out of all the systems that have been set up, this one has the most negative (lowest) energy, quite close to the transition state energy, so following the trend it should oscillate the least, but actually it oscillates the most. Looking at the skew plot, this might be because it has very little vibrational energy, and the HH atoms are quite close together (almost at equilibrium bond length), so that when the Hydrogen is pulled in towards the Fluorine, the second Hydrogen also experiences some of the electrostatic attractions and gets pulled closer as well, resulting in a very closely overlapping Lennard-Jones Potential (i.e. with only a very small 'activation energy' in-between the two minima. As a result, even though the oscillating Hydrogen has less kinetic energy, because the potential energy landscape is slightly different due to the way the particles collide, it oscillates longer before proceeding to the products.
1	-0.5	-102	Yes	These last two particles follow the same trend as before again. In fact in this one, the Hydrogen doesn't really oscillate at all, although the first HF oscillation is elongated due to the attraction of the first Hydrogen.
3	-0.5	-93	Yes	This system has the most vibrational and kinetic energy resulting in a long period of oscillation, because even as the first hydrogen is being pushed away, and the barrier between the two Lennard Jones Potentials increases, the oscillating Hydrogen still has enough energy to overcome it.

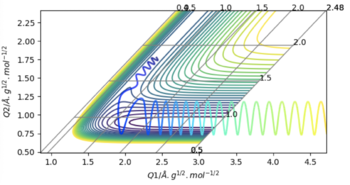
By increasing the momentum of FH to -0.8, and decreasing the overall energy of the system by making the HH momentum 0.1 we get a similar result to what occurred for a momentum of -0.6, as can be seen in the graph above, except that it is even more pronounced. In fact the HH bond seems to form again, move away form the Fluorine and only come back after a while, when the attractive electrostatic force to the Fluorine and the kinetic energy after the collision pointing the other way equilibrate. These two cases illustrate Polany's rules, which dictate that for a reaction with an early transition state (as is the case here), the vibrational energy of the molecules is ineffective in surmounting the energetic barrier compared with the kinetic collision energy (and the opposite is true for a late transition state).⁴ This is illustrated by this example as the molecules have very little vibrational energy, and only a slight increase in kinetic collision energy (due to the increase in FH momentum), which leads to a massive increase in oscillations during the transition state phase due to the increase in energy.

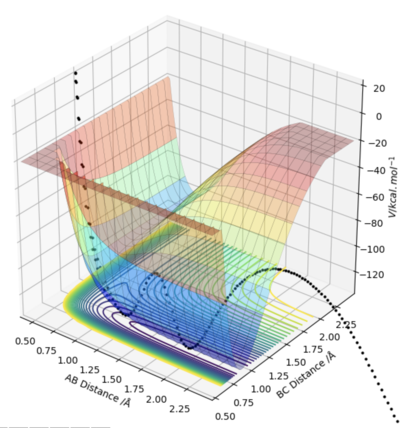
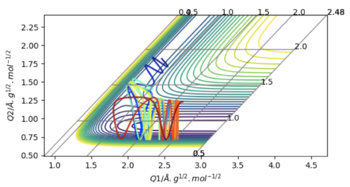
Trying to get the endothermic reverse reaction going with little HF vibrations is almost impossible, as can be seen by the graph on the right, in which the HF momentum is 0.05, and the HH momentum is -12. Even though the particles have an energy much higher than the activation energy of the forward reaction, they simply fall back down to the lower energy reactions, rather than forming the product. This again is an illustration of Polany's rule, because this reaction has a late transition state because it is very endothermic, meaning that the kinetic energy of collision has very little impact on the reaction. Vibrational HF energy is needed for this reaction to proceed.

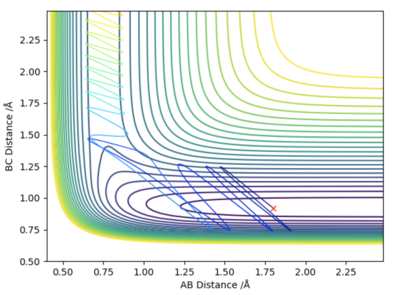
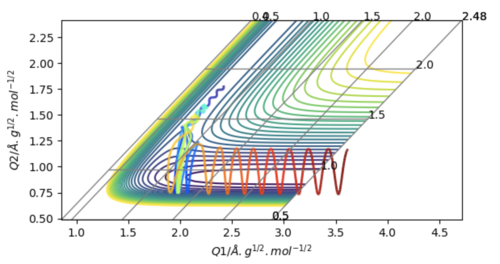
By increasing the vibrational energy we are able to make the reaction go to completion, as can be seen in the graph to the left, where the HF momentum is equal to 8, and the HH momentum is equal to -0.2.

In conclusion, it is evident that the distribution of energy in the system between translational and vibrational energy makes a very large impact on the outcome of said reaction. If the reaction has an early transition state (i.e. is an exothermic reaction), then translational energy is most important for the reaction to proceed and vibrational energy is almost negligible. On the other hand a late transition state (i.e. an endothermic reaction) means that vibrational energy is crucial for the formation of products to take place, whilst the translational energy is not effective. Hence for an exothermic reaction it is more efficient for the energy to be largely translational, whereas for an endothermic reaction it is more efficient for the energy to be mostly vibrational.

Ng611 (talk) 16:37, 7 June 2019 (BST) Good explanations.

References

¹Atkins, Peter W., et al. Atkins' Physical Chemistry. 11th ed., Oxford University Press, 2018.

²Pauling, Linus. “The Strengths of Chemical Bonds.” Archives of Biochemistry and Biophysics, vol. 59, no. 2, 1955, p. 543., doi:10.1016/0003-9861(55)90528-2.

³Schaller, Chris. “PC3. Fluorescence & Phosphorescence.” Chemistry LibreTexts, Libretexts, 23 Feb. 2019, chem.libretexts.org/Bookshelves/Organic_Chemistry/Supplemental_Modules_(Organic_Chemistry)/Reactions/Reactivity/Part_V%3A__Reactivity_in_Organic%2C_Biological_and_Inorganic_Chemistry_3/PC._Photochemistry/PC3._Fluorescence_and_Phosphorescence.

⁴Zhang, Zhaojun, et al. “Theoretical Study of the Validity of the Polanyi Rules for the Late-Barrier Cl + CHD3 Reaction.” The Journal of Physical Chemistry Letters, vol. 3, no. 23, 2012, pp. 3416–3419., doi:10.1021/jz301649w.

Reactional Dynamics

EXERCISE 1: H + H2 system

EXERCISE 2: F - H - H system

References

EXERCISE 1: H + H₂ system