MRD:01337001taw17

Molecular Reaction Dynamics: Triatomic Systems

Excercise 1: H + H₂ System

Transition States

The transition state on a potential energy surface is mathematically defined as the point where $\frac{\partial V}{\partial q_{1}} = \frac{\partial V}{\partial q_{2}} = 0$ , where V is defined as the potential energy of the system and q₁ and q₂ are orthogonal vectors where q₁ is a tangent to the reaction pathway. At this point $\frac{\partial^{2} V}{\partial q_{1}^{2}} < 0$ and $\frac{\partial^{2} V}{\partial q_{2}^{2}} > 0$ . This is because the transition state is a saddle point. It represents the maximum energy point on the minimum energy pathway between reactants and products. Good.Sw2711 (talk) 16:15, 16 May 2019 (BST)The reactants will appear as local minimums along the reaction pathway. What about the products?Sw2711 (talk) 16:15, 16 May 2019 (BST)

Finding the Transition State

Figure 1: Internuclear Distances vs Time, First Iteration

Figure 2: Internuclear Distances vs Time, Final Iteration

Figure 3: Internuclear Distances vs Time, Zoomed View of Final Iteration

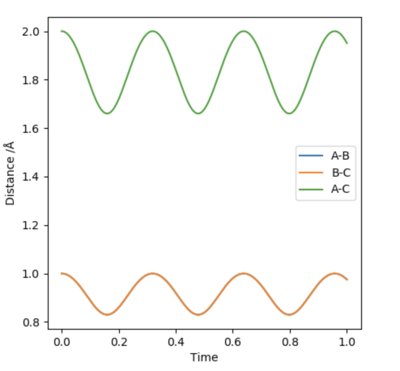
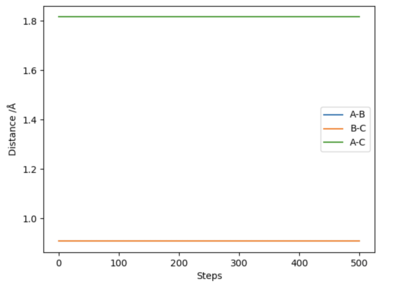
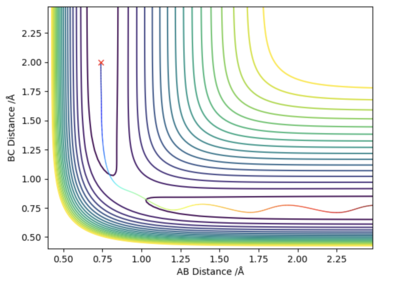
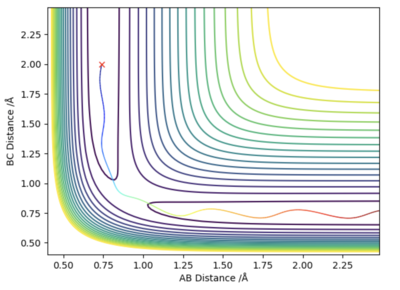
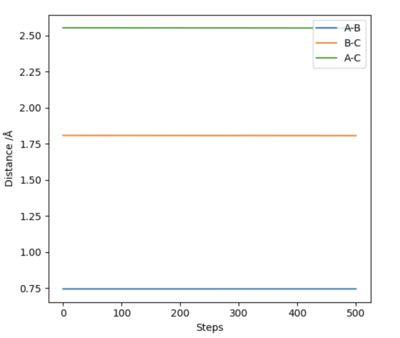
Since the system is symmetric, the transition state will occur when $r_{1} = r_{2}$ where $r_{1}$ is the distance between atom A and B, and $r_{2}$ is the distance between atom B and C. Using this condition the transition state can be located using an iterative method. A plot of internuclear distances against time can be generated as shown in figure 1. By finding the midway point between the height of the peaks and troughs a better estimate of internuclear distances in the transition state can be found. This is set as the new initial condition and the process is repeated. After three iterations, a transition state bond length, also known as r_ts of 0.908 was yielded. In the transition state for this system, the bond length will be a constant and will not oscillate. This is shown by the straight line in figure 2. Using an MEP method a very similar value of 0.9077 was generated.

Very good. You used two methods to validate your TS point! Well done!!Sw2711 (talk) 16:16, 16 May 2019 (BST)

MEP vs Dynamic Method

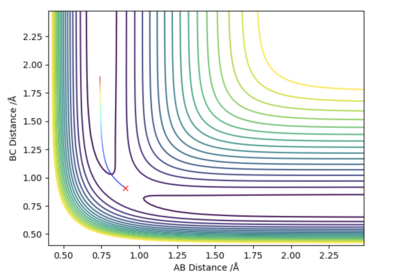
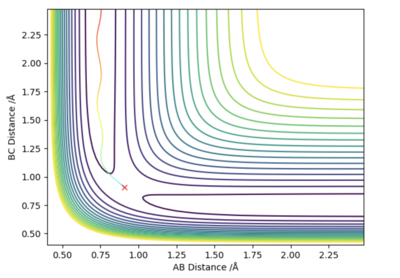
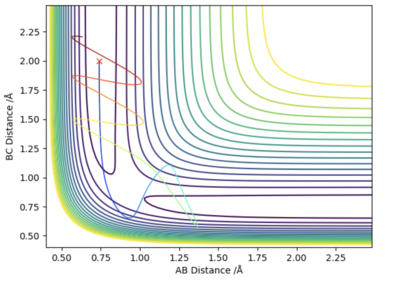
If one of the internuclear distances is set to r_ts + 0.01, the reaction will no longer remain in the transition state and instead will proceed to either the reactants or the products. A reaction pathway can then be plotted via two different approaches. As can be seen by figures 4 and 5, there are no oscillations in the minimum energy path (MEP) however there are in the trajectory predicted by the dynamic mode since it takes into account the vibrations of the molecule. The MEP is also much shorter than the path predicted by the dynamic mode. This is due to the fact that in the calculation of the MEP, momenta and velocities are reset to zero at each time step.

Good.Sw2711 (talk) 16:18, 16 May 2019 (BST)

Reactive and Unreactive Trajectories

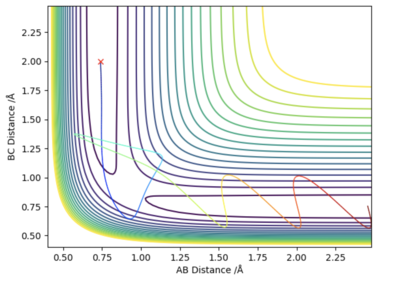
This part is good.Sw2711 (talk) 16:19, 16 May 2019 (BST) A series of scenarios were trialled to see under what conditions a successful reaction would occur. The fixed parameters used were: r_AB = 0.74 and r_BC = 2.0. Relative momenta between the atoms, p_AB and p_BC, were then changed.

p₁	p₂	E_tot	Reactive?	Description of the dynamics
-1.25	-2.5	-99.018	Yes	The reaction successfully takes place with reactants being converted to products. As can be seen, the reaction pathway goes through the transition state.
-1.5	-2.0	-100.456	No	The reaction does not take place under these conditions. This is because the reactants do not possess enough momentum, and subsequently not enough energy, for the reaction pathway to proceed through the transition state. As a result, no products are formed.
-1.5	-2.5	-98.956	Yes	The reactants possess enough momentum and energy for this to be a successful reaction. Similarly to the first scenario, the reaction pathway is able to to pass through the transition state allowing the products to form.
-2.5	-5.0	-84.956	No	The reactants have enough energy for the reaction pathway to proceed through the transition state however the reactants are then reformed. This is due to barrier recrossing. This can be seen in the corresponding contour plot.
-2.5	-5.2	-83.416	Yes	As can be seen by the contour plot, the reaction pathway actually crosses this transition state multiple times, again demonstrating barrier recrossing. The reaction however is successful and the products are formed.

From the table we can conclude that a successful reaction may not take place, despite the system having the required activation energy. As can be seen from the fourth scenario in the table, barrier recrossing is possible. It is therefore necessary that the system has the correct vibrational modes, as well as sufficient energy to cross the transition state, to ensure the products are formed.

Transition State Theory

Transition state theory, also known as activated complex theory, states that an activated complex is in equilibrium with the reactants and that the rate of product formation is dictated by the rate at which this activated complex passes through the transition state. (1) It also assumes the energy distribution of particles follows a Boltzmann distribution. (1) Despite transition state theory suggesting that reactant will not reform once the reaction pathway has gone through the transition state, as seen from scenario 4 above, this is not true. Experimentally, border recrossing is observed if the right vibrational modes are not occupied. This would lead to an experimentally lower reaction rate value when compared to the reaction rate value predicted by transition state theory.

Good. Just be aware that we only have 3 atoms in our system, so there is no Boltzmann distributionSw2711 (talk) 17:08, 16 May 2019 (BST)

Excercise 2: F-H-H System

F + H₂ and H + HF Reactions

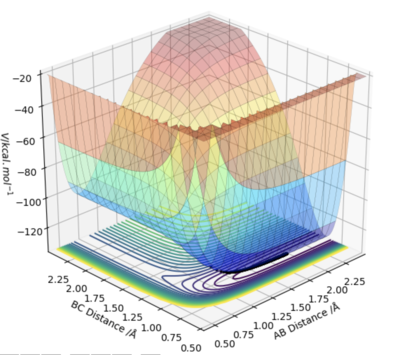
A surface plot for the reactions was plotted as can be seen in figures 6. The second reaction is just the reverse of the first reaction so the same surface plot can be used. By looking at the relative potential energy values for the start and end of each reaction, the change in energies associated with each reaction were determined. The reaction in which HF is formed was determined to be exothermic and the reverse reaction in which H₂ is formed was deemed to be endothermic. In figure 6, HF is associated with the lower plateau and H₂ with the higher one. The energy changes in the reaction occur since HF has a stronger bond than H₂. This results in energy being released when HF is formed (net energy released by HF bond formation is greater than used to break the H₂ bond) and energy being taken in when HF is being used (energy required to break HF bond is greater than the energy produced upon the formation the H₂ bond).

Good.Sw2711 (talk) 17:09, 16 May 2019 (BST)

F-H-H Transition State

By invoking Hammond's postulate, and examining the surface plot, the transition state (which will be the same in both cases) will have a structure similar to that of H₂+F. Through trial and error a good approximation of the transition state internuclear distances were found to be H-H = 0.745 and H-F = 1.808. A plot of internuclear distances is shown in figure 7.

Good. But it's better to demonstrate your strategy for your number of trials to get those values. And remember the unitsSw2711 (talk) 17:10, 16 May 2019 (BST)

Activation Energies Required for the Reactions

The activation energies were calculated by finding the difference between the energy of the transition state and the energy of the reactants. Using the transition state parameters calculated above the energy of the transition state was worked out to be -103.75. The energy of the energy of the reactants H₂ + F was found to be -103.93, and the energy of the reactants HF + H was -133.94. As a result the activation energies are 30.2 and 0.2 for the formation of H₂ + F and HF + H respectively.

Good. Again, I know you understand it, but it's better to explain how to get the energy for reactants/products. What kind of settings did you use? And the units.Sw2711 (talk) 17:12, 16 May 2019 (BST)

Reaction Dynamics

In the reaction between H₂ + F, heat is generated by the reaction. Energy is conserved however. As can be seen by figure 8, translational energy is converted into vibrational energy. The changes in energy could be probed via bomb calorimetry (in which the temperature changes are measureed) or via emission IR spectroscopy.

Good. Translational energy is converted to vibrational energy, but does that mean they are conserved? What about the potential energy then? And you need to explain a bit more about the experimental techniques you suggested.Sw2711 (talk) 17:14, 16 May 2019 (BST)

The reaction in which HF + H was formed, was further investigated with the following parameters: r_HH = 0.74, p_FH = -0.5 and r_FH = 2. The p_HH was varied in the range -3 to 3. As can be seen from the table above, the reaction is only successful for some p_HH values.

p_HH	Reactive?
-3	No
-2.95	No
-2.9	No
-2.85	No
-2.5	No
-2	Yes
-1.5	Yes
-1	Yes
-0.5	Yes
0	Yes
0.1	No
0.5	No
1.0	No
1.5	No
2.0	No
2.5	No
2.85	Yes
2.9	Yes
2.95	Yes
3.0	No

Figure 9: F-H-H Transition State Internuclear Distances

However, if the p_FH is changed to -0.8 and the p_HH = 0.1, the reaction is successful. This shows that by increasing the kinetic energy of the system the reaction outcome changes from being unsuccessful (see table above, p_HH = 0.1) to being successful.

The endothermic reaction in which H₂ + F is formed is possible despite H-F having such a strong bond strength. It is possible if the parameters are set to: r_HH = 2, p_HH = -0.01 and r_HF = 0.913 and p_HF = -10. The reaction pathway can be seen in figure 9. In order for the reaction to be successful a high vibrational energy is required.

The above are examples of Polanyi's rules. For exothermic reactions with an early transition state, the success of a reaction is more likely given a higher translational energy in the system. This can be seen in the above example where changing p_FH from -0.5 to -0.8 (i.e. increasing the kinetic energy of the system) meant the reaction when p_HH = 0.1 went from being unsuccessful to being successful. If the transition state is late however, the reaction efficiency is increased with increasing vibrational energies.

This part is good piece of work.Sw2711 (talk) 17:16, 16 May 2019 (BST)

References

(1) Atkins, P. and De Paula, J. (n.d.). Physical chemistry. 7th ed.